Physicist: When a photon with an unknown polarization hits a polarizer it has a 50% chance of being stopped and a 50% chance of going through. However, once the photon has passed through a polarizer then its polarization is known (it’s known if it doesn’t pass through as well, but it’s also destroyed). So if it passes through a vertical polarizer, then it is now definitely vertically polarized, and will pass through additional vertical polarizers no problem (as opposed to being stopped 50% of the time).
A series of identically oriented polarizers in a row is an example of a “repeated measurement”. One of the phrases that plays on loop in the back of every physicist’s head is “repeated measurements yield the same result”. This is the sort of thing that refers too.

Two polarizers arranged vertically and arranged diagonally (and perpendicular to each other). The polarizers on the left are a little dark because about half of the ambient light is stopped.
Photons (and particles in general) come in two basic flavors: definite state and indefinite state. After passing through the first polarizer a photon will be in a definite state (definitely polarized in the same direction as the polarizer). The spooky thing about indefinite states is that they’re actually in both polarizations at the same time (like Schrödinger’s cat, or particles taking multiple paths in the double slit experiment), as opposed to the polarization merely not being known. Take a moment to ponder…
Normally the polarization of one photon has nothing at all to do with the polarization of another. However, by using slickness (there are several methods), photons can be prepared in pairs so that 1) both measurements are the same, and yet 2) both photons are in indefinite states (both horizontal and vertical).
These specially prepared photons are “entangled”. Entanglement is a property that any particle can have (not just photons), and more complicated forms can be shared by an arbitrary number of particles.
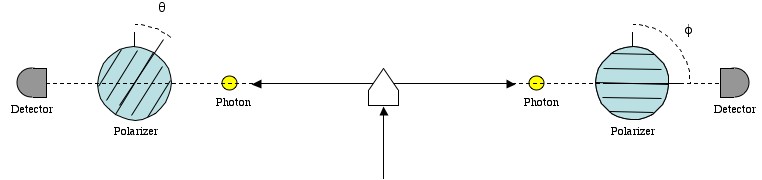
A down-converter (one way to produce an entangled pair) throws two entangled photons in opposite directions. When measured the same way by polarizers, these entangled photons always yield the same result.
Entanglement requires that the particles be in an indefinite state. If you prepare two photons to be diagonally () polarized (a definite state) then they both have a 50% chance of passing through either a horizontal or vertical polarizer (and 100% chance of passing through a diagonal polarizer like this:
, and 0% chance of passing through a diagonal polarizer like this:
). However, if one photon passes through a vertical polarizer, it has no bearing on the other. They’re in the same state, but they are not entangled.
Entangled photons always give the same result for the first measurement, so long as the two polarizers are oriented in the same direction; both vertical, both diagonal, whatevs. However, as soon as either photon is measured, you’ll find that they are both in exactly the same (no longer entangled) state. If you keep measuring the same polarization, the photon will keep going through (repeated measurements). However, if you start measuring with different orientations, there is no longer any reason for the photons to always give the same result (the way they did when entangled).
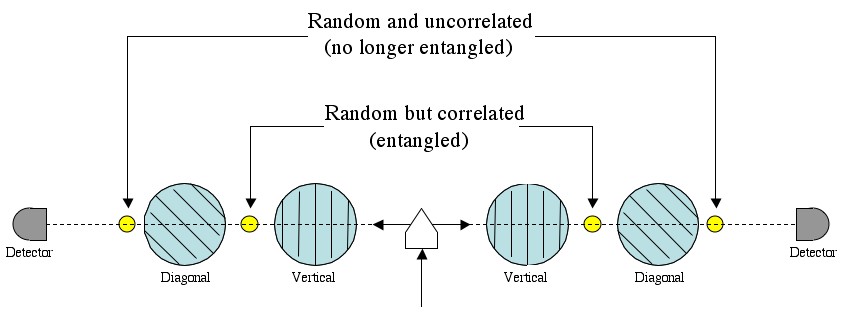
Entangled photons always yeild the same result for the first measurement. However, the first measurement destroys the entanglement. Subsequent, different measurements have random results.
If you want to impress your friends and family with vocabulary, the process of breaking entanglement is called “decoherence”. It’s the big problem with getting quantum computers off the ground. I get pretty excited about entanglement and whatnot, so what follows is answer gravy.
How the (fairly easy) math is done:
A photon that is vertically polarized can be written as and horizontally as
. This weird looking notation doesn’t mean anything profound. It’s basically saying “look! some kind of quantum state!” As it happens, a diagonally polarized photon can be described as
which is just a technical way of saying “up and to the right is half up and half to the right”. The other diagonal polarization is
.
The chance of finding a photon described by in a state
is given by
, where
is the angle between the two states. For example, the chance of finding a vertically polarized photon in the horizontal state is
impossible, which is what you would expect. The chance of a diagonally polarized photon being detected as vertical is
.
Another way of doing exactly the same thing is:
Now say you have two photons (A and B) that are vertically polarized, you’d write it this way:
Where the A and B subscripts indicate which particle you’re talking about in that bracket.
Here’s how you would write the state of two diagonally polarized photons:
Holy crap! This is just another way of saying that the chance of measuring any combination of vertical and horizontal polarization is equal. Check it! The probability of A being vertical and B being horizontal is:
Notice that the “A” parts and the “B” parts leave each other alone.
Now here’s an example of a Bell state:
(For succinctness you can write this: , just be careful to keep track of which is A and which is B.) This says that the chance of both photons being vertically polarized is 1/2, and the chance of both of them being horizontally polarized is also 50%. Even though this Bell state looks like diagonal polarization, it’s not. A diagonal state is definite:
If you measure this using vertical/horizontal polarizers you’ll find that the photon has a 50/50 chance of passing through, which seems like an indefinite state. However, using diagonal polarizers you’ll find that this is definitely a “upright/downleft” polarized photon.
If you rewrite the Bell state in terms of diagonal states (right now it’s written in terms of vertical/horizontal states) you get:
So the Bell state will also always yield the same result for both photons when measured diagonally. Isn’t that weird?
Now say you fire a pair of entangled photons in this state at a pair of vertical polarizers. If one goes through, they both go through and you’re left with a definite state:
Which in terms of diagonal states is:
Which means an equal chance of any combination of measurements! No correlation! No entanglement! That mother decohered!
By the by, for fermions (which includes protons, neutrons, and electrons) the important state is “spin”, not polarization. And for fermions the probability of a particle which is known to be in the state being measured in state
is
, where
is the angle between the axis of the spins. Without going into detail, the
term is essentially due to the “half integer spin” of fermions, as opposed to the “integer spin” of photons.







Pingback: Q: Copenhagen or Many Worlds? « Ask a Mathematician / Ask a Physicist
How would entangled pairs behave if one particle passed beyond the event horizon of a black hole? Could this be used to retrieve information about the state of a particle on the other side of an event horizon?
Naw.
Entanglement isn’t any more than a weird kind of correlation. Say you have two coins that are completely random on their own, but always give the same results as each other. If you destroy one, you’re left with one completely random (and not at all special) coin. It’s the same with dropping one half of an entangled pair into a black hole.
The weird properties of entangled particles never become apparent until the results of the measurements of each can be brought back together and compared.
But you’re not technically destroying the particle, so would it not be possible to use this assumption to predict the state of the other particle? Does the correlation break down at the point we can no longer measure the state of both particles, and is this just a limitation of observation rather something that affects the properties of the particles?
You could predict the state of the particle that fell into the black hole, but there wouldn’t be much point.
After looking at you’re own particle you could say “that other particle (that no one will ever see again) is definitely in state X”.
” However, by using slickness (there are several methods), photons can be prepared in pairs so that 1) both measurements are the same, and yet 2) both photons are in indefinite states (both horizontal and vertical).”
Just to make sure I understand this statement correctly, when they are observed do we find that one is horizontal and the other vertical? If so, how( maybe why? ) does that help us? How do we apply this concept to something meaningful?
I have been struggling to understand that about quantum computers. Being old fashioned everything is either true or false to me( not both ) and it makes perfect sense. I read that this will help with computational intensive tasks such as factoring large numbers. This may not be your realm and if not I apologize!
@Zack
With two particles in a “maximally entangled state” you can either have their results exactly correspond, or exactly not correspond. What you’ve described in the second of the two situations. They’re just two different forms that entanglement can take.
Right now the killer app for entangled particles is “quantum encryption”, which is more correctly called “quantum key distribution“. When two parties measure a string of entangled particles they always get the same result as the other, and yet the results are random. This means that they each get the same set of random 1’s and 0’s. This random string can then be used as a “one time pad” so that the two parties can communicate securely.
The advantage of entangled particles is: 1) the results are perfectly random and 2) any eavesdropper will break the entanglement and be detected.
Right now the largest distance that entangled photons can be sent is about 150km, but despite that plans are in the works to build large scale quantum networks for a variety of purposes (not just encryption).
The largest ensemble of entangled particles to date is 14. Together they can be used as a rudimentary quantum computer, but full sized, stable quantum computers are still a ways off. If you’re wondering how those might work we’ve done a couple of posts on them!
How does quantum computing work?
How can quantum computers break encryption?
Thanks for your response and the links! I am still going through a lot of the posts here! I have a follow up question if you don’t mind though.
Is the random number really random? Or is it a function like it is today? The reason I ask is because if it is a function then it would be possible to reproduce that random number wouldn’t it?- assuming you know the function
For example, what is to stop the eavesdropper from intercepting the message, measuring the string(get the key), and then send a spoofed message that will result in the same key when measured by the receiving party? The receiver is only getting a series of photons so whether they are entangled or not doesn’t matter at this point does it? It just needs to measure as the original did so that the future messages can be decrypted correctly right?
” I get pretty excited about entanglement and whatnot, so what follows is answer gravy”
I get the same way when thinking about the possibilities! Such as “plans are in the works to build large scale quantum networks”.
Pingback: Entanglement omnibus! | Ask a Mathematician / Ask a Physicist
Very illustrative, thanks !!
Can everyone agree that anything moving with speed higher as light must use 5th (or higher) physical dimension, which should have explanation in Kaluza–Klein theory for 5th dimension description?
I’m not sure I agree with your definition of superposition
Given that the solution to Schrodinger’s equation (if the Born Interpretation is correct) is a probability amplitude or to make it more clear the square root of a probability density function. Then all any quantum superposition amounts to is a superposition of possibilities the probability of one being realised on measurement given by the square of the coefficient. Schrodinger’s cat isn’t physically occupying a limbo between being alive or dead all it amounts to is that 50% of the time we will observe the cat being alive or dead.
Similarly with the Bell State all that says is that 50% of the time a photon at one detector will be measured up whilst we know automatically the other one will have the opposite spin. If we change the polarisation during the time of flight then all that does is affect the polarisation of the photon at a given detector ie reduce or increase the probability of a photon passing through
It is a statistical thing not an actual physical one
Take me off your mailing list