Physicist: It’s a little surprising that this question didn’t come up earlier. Unfortunately, there’s no intuitive way to understand why “the energy of the rest mass of an object is equal to the rest mass times the speed of light squared” (E=MC2). A complete derivation/proof includes a fair chunk of math (in the second half of this post), a decent understanding of relativity, and (most important) experimental verification.
So first, here’s an old physics trick (used by old physicists) to guess answers without doing any thinking or work, and perhaps while drinking. Take everything that could have anything to do with the question (any speeds, densities, sizes, etc.) and put them together so that the units line up correctly. There’s an excellent example in this old post about poo.
Here’s the idea; energy is distance times force (E=DF), and force is mass times acceleration (E=DMA), and acceleration is velocity over time, which is the same as distance over time squared (E = DMD/T2 = MD2/T2).
So energy has units of mass times velocity squared. So, if there were some kind of universal relationship between mass and energy, then it should depend on universal constants. Quick! Name a universal speed! E=MC2
Totally done.
This is a long long way from being a solid argument. You could just as easily have E=5MC2 or E=πMC2 or something like that, and still have the units correct. It may even be possible to mix together a bunch of other universal constants until you get velocity squared, or there may just be a new, previously unknown physical constant involved. This trick is just something used to get a thumbnail sketch of what “looks” like a correct answer, and in this particular case it’s exactly right.
For a more formal derivation, you’d have to stir the answer gravy:
Answer gravy: This derivation is going to seem pretty indirect, and it is. But that’s basically because E = mc2 is an accidental result from a more all-encompassing theory. So bear with me…
The length of regular vectors, (which could be distance, momentum, whatever) remains unchanged by rotations. If you take a stick and just turn it, then of course it stays the same length. The same holds true for speed: 60 mph is 60 mph no matter what direction you’re moving in.
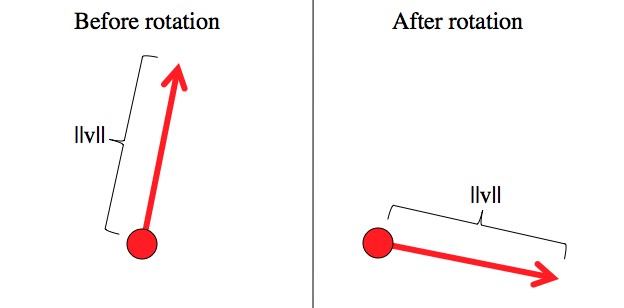
Although the vector, v, changes when you rotate your point of view, its length, ||v||, always stays the same.
If you have a vector (x,y,z), then it’s length is denoted by ““. According to the Pythagorean theorem,
.
When relativity came along, time suddenly became an important fourth component: (x,y,z,t). And the true “conserved distance” was revealed to be: . Notice that when you ignore time (t=0), then this reduces to the usual definition.
This fancy new “spacetime interval” conserves the length of things under ordinary rotations (which just move around the x, y, z part), but also conserves length under “rotations involving time”. In ordinary physics you can rotate how you see things by turning your head. In relativity you rotate how you see things in spacetime, by running past them (changing your speed with respect to what you’re looking at). “Spacetime rotations” (changing your own speed) are often called “Lorentz boosts“, by people who don’t feel like being clearly understood.
You can prove that the spacetime interval is invariant based only on the speed of light being the same to everyone. It’s a bit of a tangent, so I won’t include it here. (Update 8/10/13: but it is included here!)
Some difficulties show up in relativity when you try to talk about velocity. If your position vector is , then your velocity vector is
(velocity is the time derivative of position).
But since relativity messes with distance and time, it’s important to come up with a better definition of time. The answer Einstein came up with was , which is time as measured by clocks on the moving object in question.
is often called “proper time”. So the better definition of velocity is
. This way you can talk about how fast an object is moving through time, as well as how fast it’s moving through space.
By the way, as measured by every one else on the planet, you’re currently moving through their time (t) at almost exactly 1 second per second ().
One of the most important, simple things that you can know about relativity is the gamma function: . You can derive the gamma function by thinking about light clocks, or a couple other things, but I don’t want to side track on that just now.
Among other things, . That is,
is the ratio of how fast “outside time” passes from the point of view of the object’s “on-board time”. So now, using the chain rule from calculus:
.
For succinctness (and tradition) I’ll bundle the first three terms together:
Now check this out! Remember that the spacetime interval for a spacetime vector with spacial component , and temporal component
, is
.
(This used a slight breach of notation: “” is a velocity vector and “
” is the length of the velocity, or “speed”)
The amazing thing about “spacetime speed” is that, no matter what v is, .
(Quick aside; it may concern you that a squared quantity can be negative. Don’t worry about it.)
Now, Einstein (having a passing familiarity with physics) knew that momentum () is conserved, and that the magnitude of momentum is conserved by rotation (in other words, the direction of the momentum is messed up by rotation, but the amount of momentum is conserved (top picture of this post). He also knew that to get from velocity to momentum, just multiply by mass (momentum is
). Easy nuf.
So if ordinary momentum is given by the first term (the “spacial term”): , then what’s that other stuff (
)? Look at the conserved quantity:
What’s interesting here is that m2c2 never changes, and P2 only changes if you start moving. For example, if you were to run as fast as a bullet (in the direction of the bullet), you wouldn’t worry about it hurting you, because from your perspective it has no momentum.
So whatever that last term is () it’s also conserved (as long as you don’t change your own speed). Which is interesting. So the ‘Stein studied its behavior very closely. If you take its Taylor expansion, which turns functions into polynomials, you get this:
The second term there should look kinda familiar (if you’ve taken intro physics); it’s the classical kinetic energy of an object (1/2 mv2) divided by c. Could this whole thing (thought Einstein) be the energy of the object in question, divided by c? Energy is definitely conserved. And, since c is a constant, energy divided by c is also conserved.
So, multiplying by c: .
You can also plug this into and, Alaca-math! You get Einstein’s (sorta) famous energy/momentum relation:
.
Notice that the energy and momentum here are not the classical (Newtonian) energy and momentum: and
. Instead they are the relativistic energy and momentum:
and
. This only has noticeable effects at extremely high speeds, and at lower speeds they look like:
and
, which is what you’d hope for. New theories should always include the old theories as a special case (or disprove them).
Now, holy crap. If you allow the speed of the object to be zero (v=0), you find that everything other than the first term in that long equation for E vanishes, and you’re left with (drumroll): E=mc2! So even objects that aren’t moving are still holding energy. A lot of energy. One kilogram of matter holds the energy equivalent of 21.4 Megatons of TNT, or about 1500 Hiroshima bombs.
The first question that should come to mind when you’ve got a new theory that’s, honestly, pretty insane is “why didn’t anyone notice this before?” Why is it that the only part of the energy that anyone ever noticed was ? Well, the higher terms are a little hard to see. Up until Einstein that fastest things around were bullets moving at about the speed of sound. If you were to use the “
” equation for kinetic energy you would be exactly right up to one part in 20,000,000,000,000,000. All of the higher terms are divided by some power of c (a big number), so until the speed gets ridiculously high they just don’t matter.
But what about the mc2? Well, to be detected energy has to do something. If somebody flings a battery at you, it really doesn’t matter if the battery is charged up or not.
Side note: This derivation isn’t a “proof” per say, just a really solid argument: “there’s this thing that’s conserved according to relativity, and it looks exactly like energy”. However, you can’t, using math alone, prove anything about the outside universe. The “proof” came when E=mc2 was tested experimentally (with particle accelerators ‘n stuff).
But Einstein’s techniques and equations have been verified as many times as they’ve been tested. One of the most profound conclusions is that, literally, “energy is the time component of momentum”. Or “E/c” is at least. So conservation of energy, momentum, and matter are all actually the same conservation law!







Why is ||(ymv,ym)||² equal to (y²v² – y²c²). Where did the c² come from?
Why does the gamma term disappear in the energy/momentum equation? It was there in the equation you used to derive it.
All the other stuff was quite understandable after a couple of re-readings. Thank you.
The c2 comes from the definition of the spacetime interval. Which in turn is derived from the fact that the speed of light is the same to everyone. Specifically, the spacetime interval between the time/location of where the light is emitted to the time/location that it is absorbed is always zero (you have to plug in a quick example for that to makes sense).
The y’s are absorbed into the definition of energy and momentum.
I wrote an extra paragraph or two to clear it up. Let me know if it is actually any clearer.
I’m not worried, but I am curious. The only way a squared term comes out negative is via i. Is there a relationship (interesting or otherwise) between time and the complex numbers, or is that a non-issue?
So long as you’re not worried.
You sometimes see time represented by an imaginary quantity. Sometimes the interval is written with the time component positive and the space component negative, so that in examples like this you get positive spacetime intervals. But it’s not an issue one way or the other. The only important thing is that it’s invariant for all observers.
Pingback: Linkblogging For 07/03/11 « Sci-Ence! Justice Leak!
Brian Cox and Jeff Forshaw wrote a book with exactly that title which I can recommend.
Pingback: Interesting Reading #711 – 3D smartphone, new Galaxy tablets, full face transplant, dying cosmonauts and much more! – The Blogs at HowStuffWorks
“Take everything that could have anything to do with the question (any speeds, densities, sizes, etc.) and put them together so that the units line up correctly. ”
This reminds me of an old xkcd strip.
http://xkcd.com/687/
Pingback: Q: How do velocities add? If I’m riding a beam of light and I throw a ball, why doesn’t the ball go faster than light? | Ask a Mathematician / Ask a Physicist
is there anything in all of known existence to have a definitive point in which it does not move.? i mean think about it, everything that we know of is always in motion ,the stars, galaxies, universes , planets, etc., etc..
Frustratingly, there’s no difference at all between moving and not moving. The only distinctions that exist (in any physically meaningful way) are moving or not moving with respect to something else.
At the same time, everything always thinks it’s stationary with respect to itself. For example: I’m stationary. All those stars and planets and other falderal are moving with respect to each other, but if you were to “ask” any of them individually they’d say they were roughly stationary.
In a black hole, mass and energy are reduced to zero. does this mean that the actual equation should be E = MC2/G.
G being universal gravity.
I do not understand the math, but thinking logically maybe
E = M ( (C/G)2)
makes more sense.
Physicists (other physicists) like to use big, exciting language and often say things like “black holes destroy matter”.
But they don’t destroy matter, they just concentrate it. All the matter and energy that falls into a black hole are still accounted for in every physical way that counts.
“E=MC2” doesn’t need a fix to take into account black holes.
my point was that light cannot escape from a black holes gravity well, so it is no longer travelling at “light speed”
My mistake.
Even when light is falling into a black hole, or failing to escape it, it’s still moving at light speed. A big part of how spacetime is twisted up and curved in gravity wells seems to be the universe’s obsessive need to always keep light speed the same.
I can show you that how a particle shows wave nature
Pingback: Q: Does light experience time? | Ask a Mathematician / Ask a Physicist
merci
Why do others claim c2 is time or a catullus, when the basic math is not complete. C2 is speed which is movement which is energy. Algebra does not allow energy to be on both sides of the equal sign.
Algebra on it’s own doesn’t know what energy is. There’s no problem with energy being on both sides. In fact, if one side is energy (or, anything really) then the other side has to be the same thing. They’re equal after all!
try again
How can energy on both sides be equal when one side is the speed of light squaired time Mass is equal to an unknown value of energy?
It’s definitely not obvious (hence the post).
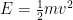 ,
,  ,
, 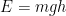 ,
, 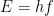 , and most famously
, and most famously  . Each equation corresponds to a different situation. In this case what “
. Each equation corresponds to a different situation. In this case what “ ” is (usually) saying is “in those occasions when some mass is lost or gained, there is a corresponding gain or loss in energy equal to the mass difference times the square of the speed of light. You can think of it almost like a unit conversion.
” is (usually) saying is “in those occasions when some mass is lost or gained, there is a corresponding gain or loss in energy equal to the mass difference times the square of the speed of light. You can think of it almost like a unit conversion.
There are a lot of examples of equations that give the energy of a system.
How can you square the speed of light in the equation E=mc2? If nothing can go faster than the speed of light, you certainly can’t square it. It wouldn’t make sense because c is supposed to be a constant.
c is a constant, like you say. Specifically,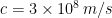 .
. . Nothing special. It doesn’t have any particular physical significance.
. Nothing special. It doesn’t have any particular physical significance.
So,
Hello there,
I am currently reading the book “why does E=MC2” and have enjoyed it greatly so far, however I have run into a snag. On page 77, two equations are given for the calculation of the length of the hypotenuse as either c^2 = a^2 + b^2 or c^2 = a^2 – b^2.
I have no idea where the second one comes from or how to intemperate it, and so I am having trouble following the logic of the chapter. I would greatly appreciate any help someone can give me in understanding what it represents or where it came from.
Thanks
Brian
Looks like they might be comparing the “Euclidean metric” (c^2 = a^2 + b^2) with the “Minkowski metric” (c^2 = a^2 – b^2). The Euclidean metric is the usual notion of distance, but the Minkowski metric is a lot trickier to build an intuition for.
If that’s what you’re book is talking about; you can derive it from the invariance of light speed, but it’s simpler to just take it as a given, that’s found experimentally.
In the equation, E^2 = m(r)^2 c^4 + p^2 c^2 where r refers to the invariant or rest mass,
in p, which refers to m v.
does m refer to the rest mass or the relativistic mass?
In relativity every m you see is rest mass!
The Physicist,
How can m in momentum be rest mass especially in relativity? Actually after I posted the question, I searched a lot and found nothing on internet. At last, I myself derived the formula for calculating relativistic mass m(0) / sqrt( 1-v^2/c^2) from the formula E^2 = m^2c^4 + p^2c^2. This can only be possible if the mass in p is relativistic mass. You only check if I am correct.
I see what you did there.
A simpler way of approaching things is to always define velocity in terms of the proper time. This makes velocity a 4-vector, which makes everything else much nicer. Doing that you find that the v term in the momentum absorbs the extra gamma, not the m.
Although, you know, tomato/tomato, potato/potato.
You’ve given the best explanation for this that I have seen or heard. Two minor points I’d like to make though. You say 1500 Hiroshima bombs is a lot of energy, but this is only, er, relative – if we were on the surface of the smallest of stars we might think 21 megatons hardly amounts to a hill of beans. The other point is that some apostrophes in some of the replies look pretty bad, though I suppose that’s relative too.
Hello I have a question
It’s been observed but not yet proved that space time
Could be bumpy and not smooth as originally thought
And evidence of this might of been found in the delay
Of individual packets of photons recieved from an super nova
Explosions . This delay could be the interaction of the photon
Within the medium that it traverses /over the distance travelled.(friction) If correct would the rate of speed for c remain the same. And if so why.
my question is: why do we subtract c2t2 from the normal spacial distance? does it mean distance that we normally observe is not the actual distance matter of fact it is that distance subtract c2t2?
second question is: In the Taylor expansion, why do we use our a=0 in part (x-a)^n?
The same reason that we use “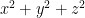 ” to define distance instead of just “
” to define distance instead of just “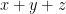 “: it works and is consistent, even if you change reference frames or rotate. The usual distance measure holds up to physical rotations, but not changing reference frames (this is seen as “relativistic length contraction”). The “
“: it works and is consistent, even if you change reference frames or rotate. The usual distance measure holds up to physical rotations, but not changing reference frames (this is seen as “relativistic length contraction”). The “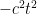 ” fixes that.
” fixes that.
You can expand around a≠0, but it would be a lot less clear what you’re looking at.
How is it that an abstract formula ( E=mc^2) can create an atom bomb?
Pingback: Everything is Relative. (Trippy) Consequences of Special Relativity. Prove E = mc2 | A Revolving Wheel
If E=mc^2, then all bodies of equal mass must have equal energy. However equal masses at different temperatures contain different energies. Contradiction?
If there is no preferred reference frame and all velocities are purely relational then how does relativistic mass work? As an example if you measured the inertia of a particle that appeared to be at rest on the surface of earth and from that calculated it’s mass, subtract the rest mass of the known matter involved then surely whats left over is the mass of its kinetic energy? I mean if Ke =1/2mv^2 then surely m=2Ke/v^2?
In which case you could perform the same experiment in a box traveling at a known velocity several times in different directions and from the difference, calculate your universal reference speed/ kinetic energy.
If velocities are truly only relative then wouldn’t the speed of light be based off your starting point? in which case the hard speed limit of the universe varies totally on when you start measuring?
Where am I going wrong here, I’ve thought myself into a very strange place.
I think the explanation is quiet normal level .. but here is lots of things missing that was not mention , like E^2 …. what i believe the momentum let say its similarly have its own energy because when particle is moving its getting its own energy .. now since two energy such as mc’ s energy also momentum’s energy . we get E as E^2 .. now for to show E^2 we have to show formula of momentum as well so what basically i think the equation will be E=square root of mc^2 +pc
just who is the “physisist” done this math an his is questionable
……
If E=mc2 is the rest mass energy, does that mean a uranium atom traveling near the speed of light has a total energy of E=mc2 + 1/2mv2?
The exact expression is floating around somewhere in the middle of the post. The energy is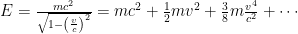 , with more and more terms that are less and less important.
, with more and more terms that are less and less important.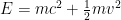 is pretty good, but isn’t exact.
is pretty good, but isn’t exact.
So, the approximation
You guys are still wrong … The correct equation is E=square root of mc^2 + pc
work on this you all will end up here i bet …
Wanna know more come here http://scifitheory.blogspot.ae/
I have a questions about how an object always seems to itself to be still by frame of reference, with everything else moving around it. If a person is moving at relativistic speeds, at a dilated ratio of vt/vT, it will seem to them that everything is moving by much faster than they recall the speed of light being able to go back when their ratio of vt/vT was 1. They will, in 8 seconds T, have traveled more than 8seconds t*C, and this amount might seem to them greater than C, while traveling .99C/t at vT/vt<1. I'm quite aware that the speed of light is relative to t, and when the traveler is no longer at relativistic speeds, the rest of the universe will have aged without them.
But this is only if spacetime is uniform everywhere. Out away from matter, in some empty expanse of the universe away from galaxies and other such falderal, where the local effect of very distant gravities affects spacetime negligibly, will it will seem to them that T is t, and .999C is 0m/s?
If so, then is t/T as controllable as velocity, provided enough energy and protection from interaction with other masses?
-from yahoo answers….hI ,I DECIDED TO ASK A REAL PHYSICIST…thanks you are great..
I KNOW THAT TIME DOES NOT EXIST.CAN SOMEONE CALCULATE E=MC2 WITHOUT THE TIME IN IT AND HOW IS THE NEW FORMULA?
Acccording to Godel’s work (friend of Einstein) time does not exist..But everubody still calculates e=mc2 with the Time in it,in spacetime and in speed of light..Can someone who knows physics calculate the formula e=mc2 without the time ,just with mass, weight speed ,distance..i believe in 21 century we can actually cancel the theory about invisible higgs field (reminds me so much of flogiston and eter in the past)..also why we cannot accept simple solution about gravity that is form of magnetism with different waves..earth has large waves,and small magnets have smaller radius waves..antimatter and dark energy does not seem to exist to me too.string theory is maybe fake..Very simple platonian notion about experience..if it is so big why i cannot see it,so conclusion does not exist.bending spacetime (if time does not exist then,there is no spacetime,nothing left to bend)..i know with my theories i disprove of part of einstein relativity,michio kaku string theory and Higg’s god particle,but what can i do..i think and have doubt..Einstein said-we have to find simple answers to problems,but not simpler..CONCLUSION:new theories about gravity..Gravity is simply magnetism,and the space galaxies will not fly away from our view one day,the space will stop expanding and will start contacting again…(oops this is against Neil de Grysse theories)..and important one that Godel allready proved it but is not widely excepted..TIME does not exist,there is no past,so you cannot travel back in time,no shortcuts no wormholes.you can travel only to the future if you travel faster than speed of light..but not in flesh as a human,you can travel only as laser beam or em wave.like a photon or neutrino..sorry for typos..i typed it fast and from i phone.
3 hours ago – 4 days left to answer.
Additional Details
explanations
KURT GODEL -FAMOUS SCIENTIST ,FRIEND OF EINSTEIN SAID THE TIME DOES NOT EXIST IN REALITY ..NOT ME..please check his work and start deep thinking.
1.if you are in space ,far away from earth you can notice Time does not exist,but EVERYTHING IS CONSTANT CHANGE.Only present moment EXISTS..(few seconds?).the atoms of every star dust,planet ,Star,galaxy and electrons are always moving ,changing positions so nothing is same every moment.
2.Time and clocks on earth are man made ,and WE OBSERVE TIME CONSIDERING EARTH ROTAIONS ,24 HOURS..MOON-MONTH,,ORBIT AROUND SUN =1 YEAR..,but all this observations are man made and if you are in deep dark space ,the kosmos you cannot observe nothing.
3.So there is only only present moment,there is no past (past is just faint memory)..so everybody wish to travel in past and FIX things better is not possible.(this could solve many phycological problems about regret and lost oportunities,guilt,missed chances)…its BETTER TO FOCUS ON FUTURE AND MAKE
30 minutes ago
3.So there is only only present moment,there is no past (past is just faint memory)..so everybody wish to travel in past and FIX things better is not possible.(this could solve many phycological problems about regret and lost oportunities,guilt,missed chances)…its BETTER TO FOCUS ON FUTURE AND MAKE IT BETTER.
4.FUTURE DOES NOT EXIST ,YET,ITS ONLY PROBABILITY OF POSSIBLE FUTURE.
5.WE CAN REPLACE CALCULATING FORMULAS WITH –VECTORS –INSTEAD OF WITH TIME
,thank you everybody for their deep thinking ,i am not pseudo scientist,, but i am studying now and preparing to enter program in university and one day be ASTROPHYSICIST
0 seconds ago
11 minutes ago
i know its hard to think and start calculating formulas with vectors instead time..and it looks stupid disproving Einstein,but if you find even a dent of hope,there is NOBEL prize in making for you!
Unthinking respect for authority is the greatest enemy of truth. -quote from actual Einstein -wiki quotes.
..this quote from him says ,never trust anybody!..believe in yourself.
47 seconds ago
According to Einstein E=mc2; where ‘E’ is the energy and ‘m’ stands for mass and ‘C’ a constant where he took it as a speed of light. But in the case of black hole we cant find out the energy produced from it unless we know the mass of it. Here we cant take the constant as speed of light because the suction power of black hole is an unknown which swallows the particles of light itself, where it blocks or destroys the medium of light to travel. Here we can assume the mass of the black hole as the mass of the object that it attracts + the mass of the black hole. Here ‘C’ is an unknown which we can assume it as an factor ‘X’ which is x times faster than the speed of the light. When we apply the equation of Einstein’s the energy that produces will be multiplied factors of these two assumptions of mass and the constant we have taken.
Pls Prove e=mc2 in easy words
It was very easy languge and short ans.