Q: How is matter created? Can we create new matter and would that be useful?

Posted on March 31, 2021 by The Physicist

Physicist: This was an interesting back-and-forth, so the original questions are italicized.

What was the energy at the start of the universe and how did it create matter?

If the question is “how much?” or “where did it come from?”, the answers are unfortunately “a hell of a lot” and “we can only guess”.  These are still very open questions. There are lots of clever guesses, but there isn’t much solid, direct data to pick out which guesses are good.

As for how it became matter, that’s “easy”: when you get enough energy in one place, new particles form spontaneously.  If the new particle has mass m, then the energy present is reduced by mc2.  This is Einstein’s famous energy/mass conversion rate: E=mc2.

Kinetic energy (the energy of movement) is the easiest way to concentrate a lot of energy in one place.  That’s why we use “particle accelerators” like CERN to slam particles together, instead of using huge lasers or lenses or anything else.  We can get individual particles moving so fast that they carry many thousands of times their mass-equivalent in kinetic energy.  When they do slam together all of that energy is released as a burst of new particles plus the kinetic energy of those (typically very fast) particles plus some light.

The trajectories of newly formed particles flying away from the collision of two gold nuclei.  When describing these events, CERN scientists inevitably make “explodey sounds” with their mouths.

The early universe was so hot that all of the particles flying around were moving at particle-accelerator speeds and new particles were generated continuously.  However, when we (people) make new particles they always appear in matter/anti-matter pairs, so how the universe has managed to have more matter than anti-matter is a mystery.

Or rather, since we’re not going to call ourselves “anti-matter”, it’s a mystery how the universe managed to not be balanced between… the two types of matter.

Is this energy stable or not, and if it isn’t how do you make it stable?

You can produce new matter with any kind of energy, so pick your favorite.  There’s no such thing as pure energy, so whatever form you choose will be one of the regular, boring types: hot water, moving stuff, light, etc. and the way you’d store it to make it stable is just as dull: charged battery, stretched spring, spinning flywheel, etc.

However, generating matter takes an colossal amount of energy.  The Hiroshima bomb was around a gram’s worth of energy.  Humanity consumes the equivalent of around 5-10 metric tons of energy per year (that’s a lot more than I had been expecting before looking it up).  You could create enough matter to make a sandwich, or you could power New York City for about a year instead.  Moral is: if you need matter, go out and collect it.

And also is it possible to contain this amount of energy in an enclosed space? (eg. a spaceship)

The greatest power source we’ll ever reasonably have access to is hydrogen to helium fusion, which converts about 0.7% of the hydrogen’s mass into energy, leaving 99.3% as helium.  So (assuming perfect efficiency), if you want to turn energy into matter, starting with more than 100 times as much hydrogen is a good place to start.

When matter falls into black holes, it tends to spiral in dense, extremely hot disks of gas first.  This gas gets hot enough that it radiates in the x-ray spectrum (the hotter something is, the bluer the light it emits and x-rays are… way to blue to see).  Under ideal conditions, matter falling into a rapidly spinning black hole can radiate the equivalent of about 40% of their mass.

This isn’t a great system.  At the end of the day, you’re throwing away matter to create the energy for less matter and you’re doing it as close as you can get to a black hole, which is a famously unpleasant place to be.

So if you want to store a lot of energy on a spacehip, it needs to have massive hydrogen fuel tanks, and if you want to use your fuel efficiently than fusion would allow, then you need a black hole too.

And what type of matter would it produce?

Newly created matter is a random assortment of all the fundamental particles it’s possible to create at the given energies.  For example, an electron (the lightest particle) has a mass equivalent of about 0.5 megaelectronvolts, which is the energy gained by a particle accelerated by half a million volts.  That means that if your accelerator uses slightly more than a million volts, then you’ll be making electron/positron pairs (positrons are anti-electrons), and if it uses less than a million volts to accelerate its particles, then you’re just making light.  It’s possible to “dial in” particular particles by carefully choosing the speed and type of the particles in your accelerator, but even then you’re not going to be creating cats and dogs or even entire atoms; just lots of individual fundamental particles.

Most fundamental particles are extremely unstable and decay very rapidly into radiation and the few stable particles: protons, electrons, and their anti-particles.  Neutrons aren’t stable on their own, but they last for about 15 minutes before decaying, which is more than enough time to use them.  So that’s ultimately the answer to what kind of matter we can create: protons, neutrons, and electrons (and their anti-particles).

When those protons and electrons are slowed down after their violent creation, you can make hydrogen or even deuterium (hydrogen with an extra neutron), but that’s the most advanced matter-creation ever achieved.  There aren’t presently any prospects for doing better.

The inevitable half of the new matter made up of anti-particles will go on to annihilate whatever normal matter it runs into, so it either needs to be thrown out or stored very carefully.  Preferably stored.  After all the trouble of creating new matter, you don’t want to just throw out half of it (destroying a bunch of perfectly serviceable matter somewhere else in the process).

And also whether oxygen will be produced?

Nope!  Or at least, almost nope.  Individual protons and neutrons, sure.  Hydrogen with some effort, yes.  But in order to create a useful amount of heavier elements, existing matter needs to be fused (through fusion).  The inside of stars is presently the only environment where it seems to be possible to create elements above helium in any abundance.  We’re nowhere remotely close to fusing elements above hydrogen in our fusion reactors.  Even the Sun is incapable of fusing helium into anything bigger.  Near the end of its life, as it runs out of hydrogen fuel and its core collapses, the Sun will briefly fuse helium, but even then it won’t make oxygen.

It’s hard to convey how difficult it is to build the atoms that go into building people.  The oxygen in the air you’re breathing right now has already had a hell of a life, born riding a supernova shock wave out of the core of a star and into interstellar space.

The natural sources of all the elements.  Artificial elements are created atom by atom, and almost everything else is made in supernovas and neutron star collisions.

Artificial isotopes can be created by bombarding existing isotopes with “slow” neutrons, some of which stick to the nuclei of the target material’s atoms.  Just like the creation of particles, this is a random and extremely inefficient process.  Technically you can make oxygen, a few atoms at a time, by using the neutrons your particle accelerator accidentally created.  But this is a long way from being a source of breathable air.

Elements (the number of protons) increases upward and the number of neutrons increases to the right.  Every isotope that isn’t black is radioactive and will decay into another isotope according to the rules in the box.  The big tool we have for making new nuclei is neutron bombardment, which moves an atom one to the right.  Starting from hydrogen, a couple of neutrons will get you to tritium (“3H” on the bottom row) which decays to helium-3 (“3He”).  With a spectacular burst of neutrons you can get a few atoms to jump helium-5 and lithium-6 (the “!!!” squares) before they decay in the “wrong direction” and then neutron bombardment and beta- decay will eventually get you to oxygen.  But not in any hurry.

So if you want to make oxygen efficiently, you really need to blow up a star bigger than the Sun.  Just start with several solar-system’s worth of hydrogen, pack it together into a star, let it simmer for a few million years until it supernovas, then collect and sort what comes flying out.  Easy.

If your spaceship is big enough to hold a black hole for power and a couple massive stars for fusion, then you can create oxygen.  But at some point you have to step back and ask what the spaceship is for.  As long as you’re slinging stars around, why not grab a nice planet to live on while you’re at it?

Posted in -- By the Physicist, Astronomy, Engineering, Particle Physics, Physics | 149 Comments

Q: Is it possible to create an “almanac” of human behavior that predicts everything a person will do?

Posted on February 28, 2021 by The Physicist

The original question was:

“Furthermore, you say, science will teach men (although in my opinion a superfluity) that they have not, in fact, and never have had, either will or fancy, and are no more than a sort of piano keyboard or barrel-organ cylinder; and that the laws of nature still exist on the earth, so that whatever man does he does not of his own volition but, as really goes without saying, by the laws of nature. Consequently, these laws of nature have only to be discovered, and man will no longer be responsible for his actions, and it will become extremely easy for him to live his life. All human actions, of course, will then have to be worked out by those laws, mathematically, like a table of logarithms, and entered in the almanac; or better still, there will appear orthodox publications, something like our encyclopedic dictionaries, in which everything will be so accurately calculated and plotted that there will no longer be any individual deeds or adventures left in the world.”

-Notes From Underground

I was wondering how these laws that Dostoevsky mentions could be catalogued. Assuming these laws that determine human behavior are indeed discovered, what could be done so that it would be easy to refer back to. If a possibility tree of some sort is devised it would be incredibly huge considering how slight adjusting of an action can completely change the result in the long run.

Physicist: Dostoevsky was writing from a very 19th century point of view; the “clockwork model” of the universe had proved to be an shockingly effective way to think about how physical principles play out.  Chemical and thermodynamic processes, complex machinery, and the motion of the planets themselves all followed extremely precise, predictable “scripts” that were being discovered in rapid succession.  For a while there it was beginning to look like all of the laws underpinning reality would soon be revealed and that the seeming chaos of the universe would be brought to heel shortly after.

And Dostoevsky may have had a point about predicting human actions.  With little more than our every movement, correspondence, interaction, and continuously updated high resolution pictures of us and everyone we’ve ever known, big data firms claim to be able to alter our opinions and compel us to buy things.

But there may yet be a little wiggle room for free will.  It wasn’t until the 20th century, with the advent of computers and some fancy math, that we had the opportunity to grapple with complexity, chaos, and the nature of randomness.

Chaos theory says that many everyday systems are unpredictable, because errors compound exponentially.  Tiny errors become small errors which become big errors which become a useless prediction.  Even if you have infinite computers, if you don’t know the initial conditions perfectly, then there’s only so much you can do.  Weather is the classic example of this.  Even though we understand the underlying laws and dynamics very well, tiny perturbations become larger and larger and quickly swamp any attempt to accurately predict the future behavior of the system.  In ten thousand years people will still be complaining about the local weather person (or clone or robot or hologram or whatever).

Chaos theory is relevant to us and our minds, because chaos is a trick that neurons picked up hundreds of millions of years ago.  Sometimes it’s important to produce a very regular predictable pattern, like the aptly named “pace maker cells” that control the heartbeat of every creature with a beating heart.  And consistency itself is important, for example if you’re a part of a society and those around you rely on that consistency.  But often it’s useful to have a ready source of unpredictability.  For example, if you need to run from an animal, it’s important to zig just as often and unpredictably as you zag.  Hunters and foragers also need randomness for certain “I have no idea where to start looking” searches.  Fortunately for us brain’d creatures, nerve cells are capable of chaotic behavior.

The chaotic nature of nerve cells implies (among other things) that when you inevitably meet a painting chimp, there’s no way to predict the quality of their art with certainty.

Noisy systems aren’t automatically chaotic.  Chaos is rooted in inherent instabilities and a sensitivity to tiny changes.  You can certainly have turbulence in water, but that doesn’t mean that fluid flow is necessarily chaotic (although it is sometimes).  On the other hand, systems like a three armed pendulum or an LRC circuit with the capacitor swapped out for a diode (to add some non-linearity) are chaotic.  We can detect the “signature of chaos” in these systems and in the responses of cells and groups of cells.

In particular we find that these systems will respond to periodic (repeating) inputs with an aperiodic output; they continuously throw themselves out of step and never quite return to the same state.  Even more symptomatic, as with other chaotic systems, nerve cells demonstrate bifurcation before they become chaotic.  As some parameter in the driving signal is increased, the neurons will follow patterns that take two cycles to complete, then four, then eight, and so on, with each bifurcation occuring sooner than the one before until they never repeat at all and become officially chaotic.

Upper Left: A sinusoidal driving voltage and the response of a single squid neuron. Lower Left: Each box is the voltage vs. rate of change in the voltage at the same point in the cycle recorded over and over and over.  Non-choatic patterns produce only one or a few dots because the pattern repeats (nearly) perfectly.  Lower Right: The stable points in the logistic graph (a very simple mathematical chaos model) vs. a changeable parameter, “r”.  Upper Right: When the “Lyapunov exponent” (a measure of instability) is negative the system is self-stablizing and repeating.  When the Lyapunov exponent is positive the system is chaotic and never repeats.  For chaotic systems, the approach and “transition to chaos” is usually pretty clear.

So there’s a good chance that brains are like weather, with climates of mentality, El Ninos of mood, and flash floods of thought.  And of course, predictable monsoons of commerce.  But while it may be possible to predict that it’s likely to rain tomorrow and you’re likely to buy an umbrella, it’s probably impossible to predict your dreams.  Remembering the way someone ate a sandwich weird, fifteen years ago, may be one of those outcrops of chaos your brain is capable of creating.  A song that always made you cry suddenly becoming funny may be as impossible to predict five seconds out as a tornado five months out.

On the other hand, we may be clockwork.  It’s hard to directly correlate the chaotic nature of isolated groups of neurons with the ever-changing large-scale behavior of people.

So here’s the point: like weather, your moment-to-moment thoughts and actions are yours alone.  Perfect prediction of a person is likely to be impossible, because neurons are capable of truly chaotic behavior.   That means that even with an atom-perfect brain scan, if the brain is chaotic, then its behavior can’t be predicted for long.

But like climate, a gross estimate of your behavior can be pretty accurate.  There are general rules, varying from person to person (which we may as well call “personality”), that can be used to roughly predict how someone will behave.  So far, the techniques that seem to work best are “getting to know someone real well” and “machine learning”.  Get a big computer to stare at lots of people as much as possible, and those behaviors it is capable of observing, it becomes somewhat good at then predicting (assuming those behaviors are predictable).

Unfortunately, machine learning algorithms tend to be “black boxes”; they work, but nobody can really say what the algorithm is doing.  It’s a little like a chef “just knowing” when to take the cake out of the oven beacuse they’ve had lots of experience.  In that sense there’s already a personalized digital “Approximate Dostoevsky Almanac” that can predict, with some accuracy, what you’re likely to do (and buy), but nobody can read it.  Even if, in theory, our brains are predictable, the almanacs we’re writing don’t mean much to those same brains.

Posted in -- By the Physicist, Biology, Entropy/Information, Machine Learning & A.I., Paranoia, Philosophical | 10 Comments

Q: How hot can a greenhouse get?

Posted on January 31, 2021 by The Physicist

Physicist: A greenhouse is a little like a “light pump” that works because of the picky transparency of glass.

The hotter something is, the shorter the wavelength of the light it radiates (it glows bluer).  The heat you feel from radiators, fires, or people is so red that it’s below the red we can see.  Hence the name “infrared”.

Most of the energy in sunlight is carried by visible light, which is arguably why we can see it (no point being able to see light that isn’t around).  Glass appears transparent to us because visible light passes through it, but visible light is only a tiny piece of the spectrum and no material is transparent to all light.  The wavelengths of the rainbow run from about 400nm for purple to 700nm for red.  Regular glass is “black” almost immediately beyond purple and not too far below red.  You can’t see the ultraviolet and infrared shadows cast by glass, but you can feel them.

The transparency of Pyrex, which is typical of most forms of glass.  The hotter something is, the shorter the wavelength of the light it radiates.  The wavelength of the light that you’re radiating right now peaks at about 9.3 microns and sunlight (because the Sun is hotter) peaks at about 0.5 microns.

Get a radiator or fire that’s big enough to feel the heat on your face, then put a piece of glass in the way; you’ll still see the fire, but your face will suddenly feel cool because it’s in a shadow.  On the other hand you still feel warmth from sunlight through a window, because the energy in sunlight is delivered by visible, not infrared, light.

A guy with a trash bag over his arm and glass over his eyes, as seen in the infrared.

So this is the key to why a greenhouse is also a hothouse.  Visible sunlight passes through the glass, heats up whatever is inside (presumably plants), and that stuff re-radiates that energy at a longer wavelength.  Instead of that light passing back through, the glass absorbs it and heats up.  Warm glass conducts heat directly into the air around the greenhouse and also radiates light like any other material.

Greenhouses: windows run amok.

The spread of heat is completely random, so the heat in the glass “wanders” toward the outside exactly as often as it wanders toward the inside.  Since the heat starts on the inside, it falls back in more often and as the glass becomes thicker.  This is just a long winded way of talking about insulation; when you wear a thick coat, the heat leaving your body is more likely to “fall out” of the coat where it went in than it is to wander all the way through.  And if you want to make a greenhouse that lets sunlight in, but loses effectively no heat to the outside, then you need to start with a laughably infeasible amount of glass.

The perfect greenhouse.  Sunlight passes through the glass, warming up things inside, and with enough glass that warmth is trapped.

Extreme insulation is a remarkably effective way to make things hot, as long as there’s at least a little heat coming from the inside.  That’s why big compost piles are hot inside; decomposition releases a tiny amount of heat, but when it’s well-insulated by a foot or two of material, that heat (mostly) stays where it is and adds up.  For a greenhouse, heat deposited by the visible light is basically being created inside and with enough glass it can be kept inside (or at least, it will escape as slowly as we’d like).

So, the theoretical limit to how hot a greenhouse can get is limited by the color of the glow of the things inside as they heat up.  Eventually the spectrum of their glow will overlap the “transparency window” enough that their light will pass right through and cool off the inside just as fast as the Sun heats it up.  As it happens, there’s a little math we can do.  The power-per-unit-area radiated at wavelength \lambda is given by Planck’s law,

P=\frac{8\pi hc^2}{\lambda^5}\frac{1}{e^{\frac{hc}{kT\lambda}}-1}

where h is Planck’s constant, k is Boltzman’s constant, c is the speed of light, and T is the temperature in Kelvin.  The vast majority of Sunlight fits inside of the 0.3μm to 3μm range, so (since sunlight varies from place to place on Earth and we are talking about a massive bubble of glass instead of any kind of remotely reasonable greenhouse) we can feel comfortable estimating that all of the \sim200 \frac{W}{m^2} makes it into the greenhouse.  Integrating the radiated power from the stuff inside the greenhouse over the 0.3μm to 3μm range collects all the light that can get out and tells us how fast energy escapes.

It turns out that the energy-in balances the energy-out at a little over 505K, 230°C, or 450°F.  That’s famously just about hot enough for paper to spontaneously burst into flame, so if you’re going to take in the flora, don’t bring a book and don’t stay too long.  The hottest possible greenhouse (on Earth anyway) would be more of a blackhouse.  This may not be the optimal way to protect plants from the elements.

Posted in -- By the Physicist, Engineering, Physics | 19 Comments

Q: Is π the same in every universe?

Posted on December 31, 2020 by The Physicist

Mathematician: That depends on what you mean by “universe.”  Here’s a framing:

A circle of radius R centered at a point P is the set of all points in the plane with distance R from P.  The diameter D of this circle is twice the radius, but can also be thought of as the longest possible straight-line path from a point on the circle to another point on the circle.  The circumference C of the circle is its arc length.  By definition, Pi = C/D.

We usually think about distance as “how the crow flies” and the shortest path between two points is a straight line, but think about how you might get around in a well-gridded city.  You either walk north to south or east to west.  You can turn at corners, but each moment spent walking is either purely vertical or horizontal.  If a mathematician gridded a city, we might think about (0,0) as the city center (the intersection of 0th Ave and 0th St).  What points are exactly 5 blocks away?  Clearly (0,5), (5,0), (0,-5), and (-5,0) (yes, negative streets and avenues!) have shortest distance paths of length 5.  But so do (2,3) and (-1,4).  You can convince yourself that to get to the point (a,b), you’re going to have to travel at least |a| in horizontally and |b| vertically, so the distance from (0,0) to (a,b) is at least |a|+|b| blocks, and it’s easy to see a path that gets you there in exactly |a|+|b|.  There might be many paths from (0,0) to (2,3) (consider ENENN or NENEN or NNNEE, for a few northeastern routes there), but all of the shortest ones take 5 blocks, like these.

Two points separated by a taxi cab distance of 12.  The red, blue, and yellow routes all cover 12 blocks.  The green line is the “how the crow flies” distance.

If we accept this “taxi cab” sense of distance, we can consider all of the points that have distance R from (0,0) and we would find it looks more like a diamond, since they satisfy |x|+|y| = R instead of sqrt(x^2 + y^2) = R.  The boundary is actually given by four lines: 

x+y = R

x-y = R

-x+y = R

-x-y = R

which gives the outline of a square at a 45-degree tilt.  Each of the side segments has length (in the usual sense of length!) of R*sqrt(2), but we might want to stick to our taxi cab sense of distance and instead of concluding the perimeter has length 8*R instead of 4*R*sqrt(2), the logic being the distance from (0,R) to (R,0) is 2R and we have to make 4 such trips to wind around the perimeter.  If we take two points on the perimeter (a,b) and (c,d), the distance between them will be |a-c| + |b-d|, which you can convince yourself will always be less than or equal to 2R (regardless whether your sense of length is the usual or the taxi length!) and equals 2R from one far corner to another, so we might feel comfortable calling the “diameter” of this “circle” 2R.  In this case, our taxi cab Pi would be Pi = C/D = (8R)/(2R) = 4.

Different notions of distance produce different notions of Pi.  If you know some calculus, you might get a kick out of this paper, which explores Pi as this ratio with respect to a bunch of different related distance systems, including both our usual system, this taxi system, and a spectrum that both lie on:

https://www.jstor.org/stable/2687579

If you’re committed to the usual notion of distance, then we’re stuck with the 3.14159265… business.

Physicist: There are a lot of physical constants in the universe; the strength of gravity, the strength of electric fields, the speed of light, the rate of the universe’s expansion, and on and on.  The vast, vast, vast majority of the possible combinations of values of these physical constants produce boring universes, like a single huge black hole or just diffuse clouds of hydrogen without stars.  There doesn’t seem to be a good reason for the constants to be what there are, save one: there are critters (people) running around saying things like “What’s going on?  The universe is so inexplicably balanced that I can exist and say things like ‘What’s going on?’.”

The philosophy here is a little pessimistic.  Existence isn’t kind, it just accidentally has pockets where it’s not actively mean.  For example, given the absolutely over-the-top number of planets in the universe, it’s not too surprising that at least one of them isn’t completely inhospitable and not surprising at all that we happen to live there.  The argument for there being lots of universes with different physical constants is similar.  Nobody likes either scenario a lot.  If there’s one universe that happens to be nigh-perfect then we need a lot of luck, and if we don’t want to invoke luck, then we need lots of universes.  All that to say, it’s not completely unreasonable to suppose that there are lots of universes and that π might take different values.

However, there’s a big difference between physical constants and mathematical constants.  For example, the gravitational constant (a physical constant) is G=\left(6.67430\pm0.00015\right)\times10^{-11}\frac{m^3}{kg\,s^2}, where \pm0.00015 is the uncertainty in the value of G.  That uncertainty is due to the fact that we have to measure G and no measurement is perfect.  We can’t derive its value, so we have to “ask the universe” using experiments.  π on the other hand is a mathematical constant, which can be derived.  It’s a “Platonic Ideal”, like a point, straight line, perfect circle, or any other mathematical idea.  We can imagine these things, but there are no examples of them in reality.  Mathematics is not the study of the universe, it’s the study of logic.  Math “works” because there are plenty of things that are “perfect enough” and plenty of methods for dealing with things that are “not perfect enough”.  We know that π=3.1415926535897932384626433832795028841971693993… not because some enterprising individual went out and measured it, but because a bunch of logicians told a bunch of computers how to figure it out (with the current record for most digits held by this enterprising individual).  Long story short: the value of π has nothing to do with physical reality.

The strict “circumference over diameter” definition of π can have different values depending on the nature of the space involved.  For example, in a curved space (or when restricted to a curved surface) we can measure the circumference and diameter of a circle and find that π is smaller than it should be, because the diameter has a longer trip and is longer than it “should” be.

π is the ratio of the circumference (red) to diameter, which is twice the radius (yellow).  If you’re stuck on a sphere using a small circle you find that π=3.1415… and if you use the largest possible circle you find that π=2.

All the same, the denizens of a curved spacetime don’t need to be too dumb to figure this out.  After all, space near Earth is slightly curved (that’s why we have gravity) and that hasn’t interfered with us imagining it flat (dumbness notwithstanding).  If they can imagine Platonic ideals, then with a little work they can figure out how to calculate π just like we have.  All that those other-worldly denizens would need is some notion of smooth space, since small circles in smooth space produce the usual value of π (this is basically the definition of smooth space).

So, do other universes have space like we do?  Unfortunately, we’ve got no experience with other universes and no solid evidence that they exist at all.  What we have are scientific speculations (which is what you get when a scientist guesses).  There’s no standard definition for “parallel universe”, but here are two lists of ideas.  In a nutshell there’s: 1) same universe, but far away, 2) quantum multiverses, 3) related universes with different constants, and 4) “other”.

When things are far enough away, there’s no way to affect anything over there and vice versa, so those places may as well be other universes.  But they’re not really.  Same π.

In the Many World’s interpretation of quantum mechanics the universe we live in seems to split into separate universes.  You’re in a not-special one of them and evidently they’ve got normal space.  Same π.

String theory and eternal inflation imply that new universes are constantly being formed with slightly different physical constants.  Lee Smolin’s “Fecund Universe” theory, where every new universe is a black hole from a higher universe, implies that universes literally evolve to be better at producing black holes.  I like the second idea better than the first, not because either is terribly convincing, but because it’s a cooler.  It scratches a brain itch.  That said, in both of these ideas the new universes are “built on the same scaffold” of spacetime with different numbers of dimensions perhaps, but with the usual notion of space and distance and therefore: same π.

Finally, physicists will sometimes include a catch-all to acknowledge that not everything is known and because as much as we learn, there are always (or at least often) surprises.  That’s the “other” and it’s not really worth worrying about, because… what are we supposed to worry about?  There may be universes out there with completely different notions of distance, but we wouldn’t even recognize them.  In that “maybe… somewhere… somehow…” sense, π can definitely be different.

Posted in -- By the Mathematician, -- By the Physicist, Geometry, Math, Philosophical | 27 Comments

Q: If the universe gets split in the Many Worlds Interpretation, then why aren’t all probabilities 50/50? Does stuff get spread thinner and thinner with each split?

Posted on November 30, 2020 by The Physicist

The original question from “A” was:

I’m reading Sean Carroll’s book Something Deeply Hidden, which is entirely about Many Worlds, and I’m following along for the most part, but there’s something I still don’t understand. […] Carroll considers an example in which an electron, passed through a magnetic field, has a 66% probability of being deflected upwards and a 33% probability of being deflected downwards as a result of its spin. […] if I fire one electron through the field, two universes will result, one with each outcome. Based on that one data point, I would have no ability to determine if the odds on my electron were 66-33, 50,50, 90-10, or any other distribution. I would need to fire, say, a hundred electrons in sequence and note down their outcomes. […] because this split is binary, it seems like over a hundred trials my results in almost all universes should converge towards a 50-50 distribution. A process which assigns unequal weights to two states doesn’t seem possible. Is this an example of oversimplification for a casual text?

The original question from “Laura” was:

I am reading Sean Carroll’s book Something Deeply Hidden and he finally answered a question I had, but now I am more confused.

My original question was about where the extra “stuff” (matter) is coming from if the Many Worlds interpretation is correct.  If there is an infinite number of worlds, how are we conserving energy?  This seems to go against the conservation of energy rule.   I was excited to read Carroll’s answer to the question until I learned what it was: each world gets “thinner.”  Gah!

Is this like the philosophy thought experiment: everything doubles in size every day, but so do all our measuring instruments so we will never know.  This is unfalsifiable, so provides no real information/answer.

Carroll gives the example of a bowling ball world that, when it decoheres, becomes (as an example) two bowling ball worlds.  Each bowling ball shares the original mass so they still add up to the total mass of the original bowling ball.  Now do that infinity times- and I don’t get how we can get that thin and still exist.  (Thought: Maybe this is how the multiverse ends.)

Physicist: When you watch a sci-fi series (almost any of them) at some point there’s an episode about parallel worlds, loosely justified by quantum mechanics, and ultimately just an excuse to get the actors to swap wigs.  This is how most people are introduced to the Many Worlds Interpretation and, while not exactly wrong, there are some caveats to include in the episode credits.

First a little background. If you’re already familiar with what the Many Worlds Interpretation is and don’t (justifiably) feel that it’s completely crazy, feel free to skip down to “To actually answer the questions…“.

Quantum phenomena exhibit “superposition”, meaning that they are often in multiple states simultaneously.  The first and one of the more jarring examples is Young’s double slit experiment.  A barrier with two closely separated slits is placed between a coherent light source (like a laser or a pin point) and a projection screen.  When light falls on the barrier we see a collection of bright and dark bands on the screen, instead of just a pair of bright bands (which is what you’d expect for two slits).  This is completely normal and to be expected, because light is a wave and we know how waves work.  In fact, when Young first did this experiment in 1801, he used it to accurately determine the wavelength of visible light for the first time.  The double slits genuinely couldn’t be a cleaner, easier-to-predict, example of wave-like behavior.

Send photons through the double slit barrier one at a time, carefully keeping track of where they end up, and you’ll find they still interfere like waves.

Repeat this exact experiment, but turn down the light so low that only one photon is released at a time and, as you’d expect, only one photon impacts the screen at a time.  But terrifyingly, when we keep track of where these individual photons arrive, we find they line up perfectly with how intense the light was when it was turned on fully.  Each photon interferes with itself, creating a pattern identical to that created by a wave going through both slits.

The double slit experiment, in a very non-unique, non-special way, shows that quantum phenomena have two different sets of behavior.  When light is passing, undetected, through both slits we say that it’s “wavelike” and is in a “superposition” (it’s in multiple places/states).  When the light impacts the screen and is detected we say that it’s “particlelike” and is in a “definite state”.  “Wavelike” is an old term, and the one most likely to sound familiar, but the fact that a photon behaves specifically like a wave isn’t nearly as important as that fact that it managed to go through both slits.

Superposition is one of those things we absolutely cannot escape.  Although there are plenty of disagreements at the fringe of quantum theory (as there ever should be), the idea of superposition is not one of them.  It’s bedrock.  It would be like competing climatologists arguing about whether rain falls up or down.

“Wave/particle duality”, the juxtaposition of superposition and single-position, is at the heart of the “measurement problem”, which asks why these two behaviors exist, what makes them different, and what gives rise to them.  In particular, since every isolated system seems to be operate in superpositions, what is it about measurements that causes those many states to “collapse” into just one?

Making the measurement problem especially problematic, and pushing us closer to the realm of philosophy, is the fact that without exception every investigation into the limits of quantum phenomena has told us that there doesn’t seem to be one.  We’ve established entanglement between continents, kept objects (barely) big enough to be seen in superpositions of mechanically vibrating states, performed the double slit experiment on molecules with thousands of atoms, … the list doesn’t end.  The difficulty in demonstrating superposition isn’t a fundamental issue, like going faster than light, it’s an engineering issue, like going faster than sound.  Large sizes, distances, and times make manipulating quantum systems much more difficult, but not impossible.  Which forces some uncomfortable questions.  Is there some inexplicable, never-observed “collapsing effect” that forces the world around us to actually be single-stated or, if superposition is the rule, why does the world seem to be single-stated?

There are a lot of theories about what causes collapse.  Very broadly, they can be grouped into three schools of thought: “the Copenhagen Interpretation”, “the Many Worlds Interpretation”, and “shut up and calculate”.  Adherents to Copenhagen insist that the macroscopic world we see around us really is in a single state and that collapse is a real, physical thing.  Practitioners of the Many World Interpretation say that superposition is literally universal and we experience that by living separately in an effectively infinite set of “worlds”.  And finally, for most physicists the measurement problem isn’t a problem.  If you’re a geophysicist, delving philosophical questions about the weird quantum properties of the semiconductors in your equipment isn’t nearly as important as that equipment working.  The “shut up and calculate” school asks and answers the question “Is there a problem?”.

The appeal of Copenhagen is that it feels right.  Maybe tiny particles can be in superpositions, but at the end of the day you’re not.  You’re you, not many yous.  The problem with Copenhagen is a lot like the problem with geocentrism (the notion that the Earth sits still in the center of the universe).  We can see lots of moons, including ours, orbiting exactly in accordance with Newton’s laws of gravity and motion.  But the planets move in wildly swinging paths under the influence of inexplicable forces, while the Earth inexplicably sits still.  That’s two very different systems floating around in a bunch of “somehow it works out”.

Left: The Galilean Moons of Jupiter are a great model of the solar system, orbiting in the same plane along elliptical paths. Right: Applying the same rules to everything in the solar system at large, we can explain why Mars jogs around the sky when it’s overhead near midnight without invoking any new rules or mysteries.  The Earth is moving too.

Many Worlds is a bit like heliocentrism; everything is treated in exactly the same way under the exact same laws, with no extra inexplicable effects or special circumstances.  The problem is that Many Worlds is so mind-bending that it shouldn’t be brought up in polite company.  You don’t feel like you’re moving right now, because that’s how you should feel with the entire Earth moving right along with you.  And you don’t feel like you’re in many states, because that’s how every state should feel.  That takes a little unpacking.

In spite of the interference pattern produced by going through both, when we put a photo-detector behind each slit we find that each photon is caught going through only one.  As far as (either version of) the photon is concerned, it went through a slit, arrived at a screen, and suddenly a bunch of physicists are scratching their chins and/or yelling at each other.

But why doesn’t the photon notice the “other photon”?  An important property of quantum-ness is “linearity”, which means that the end result is always a clean sum of all of the contributing pieces.  If you and a friend each roll dice and add up the results, the dice didn’t need to know about each other or have some kind of spooky connection, even though the ultimate result requires all of the dice.  Similarly, the pattern on the screen is the sum of the contributions from the two slits, which means that the different versions didn’t need to work together or be aware of each other to create it.  The stuff being added together can be positive, negative, or even complex-valued, which is why opening the second slit actually removes light to create dark fringes, but the important thing is linearity; one state doesn’t “know” about the other.

Ripples are a linear phenomena.  The height of the water at any location is the sum of the ripples there, and yet despite working together in this way, the ripples ignore each other.

This is the idea behind the Many Worlds Interpretation: when a set of options presents itself, like going through one slit or the other, both options are taken and neither knows about the other.  For all intents and purposes, the various states of a thing exist in their own worlds from their own point of view.  That point of view is an important distinction; each version of each photon in the double slit experiment may say that they’re going through only one slit and that other versions must be in “other worlds”, but of course all of those versions are ultimately in the same room, contributing to the interference pattern we observe.

To really show how ridiculous superposition is, Schrödinger created the “Schrödinger’s Cat thought experiment”, wherein an unfortunate cat is placed in a box with a decent chance of being killed.  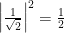Schrödinger describes how the cat can be put into a superposition of both alive and dead, like \frac{1}{\sqrt{2}}|alive\rangle_c+\frac{1}{\sqrt{2}}|dead\rangle_c, where by Born’s rule, \left|\frac{1}{\sqrt{2}}\right|^2=\frac{1}{2} indicates that each possibility has a one-half chance of being observed.

Schrödinger then sagely points out that you’ll never see that superposition in practice, because when you open the box the cat will obviously always be one state or the other.  This experiment (sans cat) is done whenever any measurement is done on a superposition of states and the single result recorded (which is frequently).  So, given that superposition is a thing, this thought experiment forces us to ask “Why does observation cause collapse?”.

Not to be outdone, Wigner came up with his own thought experiment, “Wigner’s Friend” (Wigner claimed to have lots of friends, but for whatever reason, the one in his thought experiment never had a name).  The cat, the box, and Wigner’s friend are all put into an even bigger box and the Schrödinger’s cat experiment is run again.  But will the cat still collapse into a single state when observed?  The Wigner’s Friend thought experiment forces us to ask “Does observation cause collapse?”

Excitingly, this was recently done (with particles, not cats and people) and the answer is a resounding “nope!”.  If you can do a measurement entirely inside of an isolated system, then there’s no collapse; the measurer and measuree become “entangled”, but stay in a superposition of states.  Before Wigner’s Friend opens the box, the Friend-and-Cat state is a superposition, something like 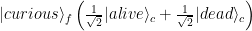|curious\rangle_f\left(\frac{1}{\sqrt{2}}|alive\rangle_c+\frac{1}{\sqrt{2}}|dead\rangle_c\right), and after the Friend opens the box, their entangled state is a superposition, like \frac{1}{\sqrt{2}}|relieved\rangle_f|alive\rangle_c+\frac{1}{\sqrt{2}}|horrified\rangle_f|dead\rangle_c.  Just like the experiment with just the cat, there’s a 50/50 chance of either pair of results, “relieved/alive” or “horrified/dead”.  In the actual experiment the experimenters had a choice between interfering the states to show that they are in superposition or simply asking the Friend what they see.

If you asked Wigner’s Friend what it felt like to be in a superposition of states, their answer would be “Um… normal?”.  So although we can’t come close to putting entire people into a superposition of states, we can infer what it feels like.  Each of the different versions of you in the superposition all feel like they’re in a single state, all have consistent personal histories, and all feel like they’re living completely normal, non-quantumy lives.

Point is, you already know exactly what it feels like to be in a superposition of states.  Way to be!

To actually answer the questions we need to look at how Many Worlds is usually presented and compare it to a nice standard quantum experiment like, just for example, the double slit experiment.  As bizarre as Many Worlds gets, it’s never about vast universes tearing apart, it’s about regular, dull-as-dishwater, superposition.

Say you needed to decide between a trip to the Moon or the bottom of the sea, but rather than flip a coin and go to one, you measure a quantum system (like Wigner’s Friend and the cat) so you can go to both.  Many Worlds folk would say “the world split in two”, one for each result and excursion.  Probability is a little hard to define in this situation, since the question “did you go to the Moon or the bottom of the sea” doesn’t have an overall answer, even though for each version it certainly seems to.

(By the way, I’m not advocating spending any money on it, but there is an app, “Universe Splitter”, that purports to measure a quantum system and report the results.  In every way it is absolutely indistinguishable from a coin flip.)

So, consider the double slit experiment.  Even though each photon goes through both slits, you can easily make it so that they go through one more than the other.  Nothing fancy, just put the light source closer to one slit than the other, or even better, make one slit wider.  You’re more likely to see a photon coming out of the wider slit when you measure, and the wider slit will have a proportionately greater influence on the interference pattern.  In this case you can easily model the skewed probability by considering many identical slits, where some of them happen to be squished together into a single slit.  In fact, in practice that’s exactly what you have to do to accurately describe the double slit pattern.

The smaller pattern is produced by the double slit interference, but the larger “beats” of the single slit pattern are due to the non-zero width of the slits.

The important thing here is that the dichotomy, the “splitting”, isn’t a thing.  Or at the very least, it isn’t what dictates probability.  The mathematical formalism behind the quantum state describes it as “a vector in a complex vector space” (it’s a long list of complex numbers).  Each number dictates the probability that a measurement will produce a particular result and whenever you have to combine two or more causes of an event, these complex numbers are what you add together.  In a very direct sense, the “quantum state vector” describes reality, what is and what isn’t.  There are arguments, halfway decent arguments, that try to justify why the quantum state vector and probabilities are related through the Born rule (taking the square magnitude of the complex value to find the probability), but ultimately this should be treated as an axiom.  It’s true in as much as it works perfectly at all times in every situation that it has ever been tested, but it’s merely assumed to be true because we can’t derive it from simpler things.

When we make measurements (quantum mechanically or not) we gain information and with that information we can change our “priors”, the things we used to determine probabilities.  For example, say you’ve rolled and covered a die.  The probability of any result is 1/6, so listing off the “probability distribution” for all six results is {1/6, 1/6, 1/6, 1/6, 1/6, 1/6}.  Now say you’ve learned that the result was odd.  All of the even possibilities disappear, but the odds are affected too: {1/3, 0, 1/3, 0, 1/3, 0}.  The distribution must always be “normalized”, meaning that the probabilities always sum to one.  This is how all probabilities are defined; not as “a true probability” but as “a probability given that…”.

Now say that the experiment is repeated with a quantum die.  The experience is exactly the same, but now every result happens.  The probabilities in the “no evens” and “no odds” worlds are {1/3, 0, 1/3, 0, 1/3, 0} and {0, 1/3, 0, 1/3, 0, 1/3}.  On the one hand you could say that the “worlds” are getting spread thinner, but in reality nothing is appreciably different before or after a measurement.  The Sun still rises, Rush still rules, and probabilities still sum to one.  You could role dice for months, getting strings of results within minutes never before seen, and the world won’t be any different than it was before you started (assuming you can get your job back and explain to your friends and loved-ones why you disappeared for months).  The results that don’t come up instantly become irrelevant as you re-normalize on move on.

A rare picture of a Yahtzee player not destroying the universe.  The rolls of the dice before don’t “thin out probability” on the rolls to come, and measurements don’t “thin out” the universe in exactly the same way.

Evidently energy and existence in general is the same way: perpetually normalized.  If not then you should be able to tell the difference pretty quick.  Say you want to shoot two targets, but only have one bullet.  You could flip a coin and shoot one, but why not measure a quantum system so you can do both instead?  If energy had to be split between universes, then you’d find that you don’t hit either target because your bullet is suddenly half-dud.

A good way to gain some insight into this, you’ll be shocked to learn, is to consider the double slit experiment.  Release one photon with X energy and exactly X energy will impact the screen.  We say that the photon goes through both slits and so it makes sense to say that the photon’s energy is spread out, with X/2 going through each slit.  However, superpositions can never be directly observed.  In the double slit experiment we infer that the photon goes through both slits based on the interference pattern.  That doesn’t mean each slit gets half a photon (photons can’t be divided), it means that this system is in a superposition of both slits having an entire photon.  This is re-normalization in the act; when you measure where you expect there to be “some photon” you either find one entire photon or the photon is somewhere else.  Even when we’re busy inferring things about the photon, we’re always talking about one, full photon.

Similarly, when we make ourselves part of the quantum system and worry about other versions of ourselves with different perspectives, we infer that those other “worlds” will also be accessing the same energy we do.  And in some sense they are.  But just like probabilities or entire photons, that energy doesn’t get watered down.  The system as a whole is in a superposition of states where all of the energy is present.  Every measurement produces a result where the exact same amount of energy exists before and after.

It’s cheap to say “that’s how the math works”, but this is bedrock stuff and there’s no digging down from here.  If you’ve gotten this far and you still don’t feel comfortable with what exactly a superposition is, that’s good.  Feynman used to get bent out of shape when anyone asked him “whys” and “whats” about fundamental things.  With regard to the weird behavior of quantum systems and why we immediately turn to the math, he said

“There isn’t any word for it, if I say they behave like a particle, it’ll give the wrong impression. If I say they behave like waves… They behave in their own inimitable way. Which technically could be called `the quantum mechanical way.’ They behave in a way that is like nothing you have ever seen before. Your experience with things you have seen before is inadequate, is incomplete. […] Well, there’s one simplification at least: electrons behave exactly the same in this respect as photons. That is, they’re both screwy, but in exactly the same way.” -Richard “Knuckles” Feynman

That simplification, by the way, is the fact that you can use quantum state vectors, superpositions, Born’s rule, and the rest of the standard quantum formalism for literally everything.  Small blessings.  Since Feynman already came up, he also has a stance on energy that is simultaneously enlightening and disheartening, but may shed a little light on why you shouldn’t be too worried about it getting “thinned out”.

“There is a fact, or if you wish, a law governing all natural phenomena that are known to date.  There is no known exception to this law – it is exact so far as we know.  The law is called the conservation of energy.  It states that there is a certain quantity, which we call “energy,” that does not change in the manifold changes that nature undergoes.  That is a most abstract idea, because it is a mathematical principle; it says there is a numerical quantity which does not change when something happens.  It is not a description of a mechanism, or anything concrete; it is a strange fact that when we calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.  (Something like a bishop on a red square, and after a number of moves – details unknown – it is still on some red square.  It is a law of this nature.) […] It is important to realize that in physics today, we have no knowledge of what energy ‘is’.  We do not have a picture that energy comes in little blobs of a definite amount.  It is not that way.  It is an abstract thing in that it does not tell us the mechanism or the reason for the various formulas.” -Richard “Once Again” Feynman

Ultimately, the Many Worlds Interpretation does yield some useful intuition.  It gives us a way to imagine a larger world where we exist in superpositions of states.  We can ponder spiraling what if’s about the other versions of us and our world.  But at the same time, it’s not entirely accurate and it does lead to some misleading intuition.  In particular, about the universe “splitting” or even being in many pieces at all.

Very, very frustratingly, without declaring a measurement scheme in advance, you can’t even talk about quantum systems being in any particular set of states.  For example, a circularly polarized photon can be described as some combination of vertical and horizontal states, so there’s your two worlds, or it can described as a combination of the two diagonal states, so there’s your… also two worlds.  This photon is free to be in multiple states in multiple ways or even be in a definite state, depending on how you’d like to interact with it.  For the world to properly “split” a distinction must be made about how the photon is to be measured, but that isn’t something intrinsic to either the photon or the universe.

In some sense, the Many Worlds interpretation is, at best, an imaginative way to roughly catalog the results of particular measurement results and not a good way to talk about the universe at large.  For that, I humble advocate “relational quantum mechanics” where the system in question, the observer, and the universe at large are all assumed to be quantum systems and how they evolve is dictated by how they interact (and what measurements they use).

Posted in -- By the Physicist, Paranoia, Philosophical, Physics, Quantum Theory, Skepticism | 12 Comments

Q: Asteroid mining. Why?

Posted on October 31, 2020 by The Physicist

Physicist: Why bother going out to mine asteroids?  Why not stay home?  The answer is a little grim.  Consider Easter Island, or Iceland, or England; each are isolated places that were once covered in vast forests with abundant animal life and which are now famously barren (those poems about the beauty of the windswept English moors should rightfully be about vast not-windy forests).  Now imagine that you and everyone you’d ever known or heard of were living on Easter Island in the waning days of its civilization.  There are a few options available: you could stick around and try very hard to cultivate the few remaining resources available, to fix everything before being adventurous, or you could start building boats.  Not to leave, but to reap the benefits that come from access to different, unimagined environments, and to dilute the impact you have on your little island.  Today, despite still having only a tiny forest and not nearly enough farmland to support it, Easter Island has a larger population and more infrastructure than ever before in its history.

For those of you reading between the lines, Earth is an island too.  But unlike Easter Island, we have to do absolutely everything “in house” and effectively no access to the outside world.  Everything humanity does directly impacts the Earth and, while that sounds like a simple truism, it doesn’t have to be.  Earth is tiny compared to the sum of planets, moons, and smaller bodies in the solar system.  While Earth has a lot going for it, it’s about the worst possible place to look for a lot of the resources that make our civilizations possible and the absolute bottom of the list for places to be cavalier with pollution.

The oldest known examples of iron tools showed up during the bronze age, before the invention of iron smelting.  When Tutankhamun died 34 centuries ago he was buried with an iron dagger, which is noteworthy for a couple reasons.  First, iron smelting (turning ore into iron) is complicated and energy intensive, which is why Egyptians didn’t start doing it until 8 centuries later.  It may have come from somewhere else and been given to the child king as a gift, but that wouldn’t explain the dagger’s peculiar alloy: a literally other-worldly 11% nickel impurity.

Left: Tutankhamun’s incredibly rare and valuable iron knife with it’s cheap-as-dirt gold sheath. Right: A metallic meteorite.  The pretty lines in the cut are “Widmanstätten patterns”, which form when iron and nickel are allowed to cool slowly over millions of years.

Metal working was invented before smelting, which is fine for gold since “metallic gold” exists on Earth.  You can literally dig it out of the ground, dust it off, and start making jewelry.  But metallic iron doesn’t naturally exist on Earth.  After billions of years stewing in our water and oxygen atmosphere, any pure iron that might have existed has rusted away and combined with rocks and minerals long before any person could have found it.  So it’s not a coincidence that the oldest worked iron show clear signs of being from space.

In fact, using a metal detector is the quickest way to find space rocks (were you so inclined).  Of course, Earth is a giant space rock made of lots of smaller space rocks, so you’d think that Earth would be just as metal rich as asteroids.  And you’d be right.  Unfortunately, Earth is mostly molten.  At one time even the surface was mostly molten and since then, through plate tectonics, huge chunks of the crust get remelted every few hundred million years.  That gives the heaviest material plenty of opportnity to separate out and sink, like dirt settling out of water.  So Earth does have a heck of a lot of heavy metals, but almost all of it is stuck in the core, starting at 3,oo0 km below your feet.  So sure, there’s a huge amount of iron, uranium, and other heavy metals in Earth, but it doesn’t really count.  Not for us anyway.  All of it is going to stay right where it is.

The same gravity that makes Earth one big rock instead of billions of small rocks makes life on Earth both possible and difficult.  Without gravity we wouldn’t have air to breathe, or oceans, or any of our favorite not-tied-down stuff.  But it does make life worse.  Ask yourself some very basic questions about mining: Why is it so hard to dig a hole and keep it from collapsing?  Why does it take so much work to get stuff out of that hole and get it where it’s supposed to go?  Gravity.

It takes a shocking amount of energy to pulverize everything in this city-sized hole, pull it to the surface, and move it overland to somewhere else.  And that’s step one.

In short, Earth is a hellscape of corrosion and gravity.  We live in about the worst possible location for mining.  The Moon isn’t ideal either; it’s also stratified with most of its metals in its core, but at least there’s no air.  Small blessings.

We’ve already mined all of the high-purity “low-hanging fruit” resources that we can find (Technically, the best iron and nickel mines are asteroid mines, they’re just ex-asteroids).  Every element has its own story and processing requirements, but in a nutshell, when you mine for something you’re digging up rocks that include what you’re looking for as just a small fraction of their chemical makeup.  For example, to get aluminum we generally dig up bauxite which is composed of aluminum, oxygen, hydrogen, and a bit of iron.  To remove the aluminum we have to break bauxite down to its atoms and chemically sort them to get aluminum by itself.  Some processes are more efficient than others, but at the end of the day there’s a cost to pay to the gods of entropy when you sort anything into its base elements.  Three buckets with aluminum, oxygen, and hydrogen have much lower entropy than a pile of bauxite, so there’s a thermodynamic limit to how good the process can be.  It will always reqire lots of work.  Pointedly for us (and everything else that lives), between the massive energy consumption, incidental poisonous by-products, and direct damage to the land, large-scale mining and industry is really, really not the sort of thing that should be done on Earth.

What we have access to here on Earth is a pittance and gathering up that pittance means scouring the surface of the Earth, which is not ideal.  When someone says “there are resources in space” it’s more accurate to say “all of the resources are in space”.  Heck, there’s more than twice as much liquid water on Europa than Earth, so we don’t even have the water market cornered.  In addition to its millions of smaller cousins, the asteroid belt hosts the exposed metallic core of a shattered protoplanet, 16-Psyche (named using a very old convention: it was the 16th asteroid discovered).  It’s over 200 km across, the size of a state, made almost entirely of heavy metals, and could satisfy just our current iron consumption (about 1.2 billion tonnes per year) for about 18 million years.  With a surface gravity of about 1.5% of Earth’s, a child could lift and throw a car’s worth of mass, so moving material around is literally child’s play.  So that’s a practically infinite supply of easily mined construction materials, nuclear fuels, and the increasingly rare elements we need for our increasingly fancy technology, in a form that’s more pure than we’ll find anywhere on Earth, and all in a place where we couldn’t destroy the environment if we tried.  And 16-Psyche is just 1% of the mass of the asteroid belt.  It’s a good place to start.

Admittedly, the asteroid belt is a long way away.  But distance isn’t the problem.  Getting around in space is embarrassingly easy; it’s leaving Earth that’s a pain.  When we think of space travel, we usually imagine huge, and more importantly expensive, rockets.  Earth, it unfortunately happens, is the hardest place in the solar system to leave (there are bigger planets, but they don’t have solid surfaces to leave from).  To achieve low Earth orbit you need to accelerate to 8 km/s, almost 24 times the speed of sound, and all of that accelerating needs to be done in just a few minutes.  Going half-way to space means being back on the ground in short order.

Jumping that lots-of-acceleration-right-now hurdle is the job of “launch vehicles”, which are always chemical rockets.  Despite all the glamour and showmanship, chemical rockets are primitive like steam engines are primitive.  The Apollo missions were sent to the Moon on a mix of refined kerosene and liquid oxygen; the sort of fuel you might throw together if your camp fire was boring.  The exhaust from that burning kerosene explodes out of the rocket bell at 2.5 km/s, which could stand to be a lot faster.  Unfortunately, if you need high-thrust right now, there aren’t presently any other options.  NASA made up for the sluggishness of their propellant by using a lot more of it.

To state the obvious: there’s a lot of stuff flying out of that thing.

But once you’re in space, you can take your time and use ion drives.  They’re not as clumsy or random as a rocket; an elegant engine for a more civilized age.  Ion drives fire off their propellant on the order of ten times faster than chemical rockets and that’s a really big deal.

When you use propellant, you’re not just moving your rocket, but the propellant you’ll be using later.  So if you can use that propellant more efficiently, by throwing every bit of it as fast as possible, then you not only need less it to move your spacecraft, you need less propellant to move less propellant.  The gain in efficiency is exponential as the rocket equation makes explicit; the ratio of the spacecraft-and-fuel’s initial to final masses is \frac{M_i}{M_f} = e^{\frac{\Delta V}{V_e}}, where ΔV, “delta vee”, is the change in speed the rocket is capable of and Ve is the velocity of whatever the rocket is throwing out the back.

Left: Von Braun next to one of the chemical rocket engines of the Saturn V, a launch vehicle. Right: Faceless engineers next to the Dawn probe, a spacecraft.  Over eleven years, Dawn’s solar powered ion drive used less than half a ton of xenon to accelerate a total of 11 km/s as it investigated multiple targets in the asteroid belt.  That’s faster than the Saturn V.

The Dawn spacecraft traveled to and orbited both Vesta and Ceres, the second and first largest asteroids in the belt.  Being the first to do it makes Dawn a first-generation rock-hopping spacecraft.  We can reasonably expect the spacecraft that will eventually move around in the belt will be at least this capable.

What Dawn did, with its fancy-dance ion drive, when it got to Ceres.  It’s clearly not 2025 yet, but it ran out of fuel two years ago (Halloween 2018), so we can be reasonably confident about where it will be in the future.

Being able to use ion drives and gravitational slingshots spells the difference between compact, efficient, long range “spacecraft” and bloated, wasteful “launch vehicles”.  Traveling between planets and across the solar system is genuinely much easier, safer, and eventually cheaper than clawing your way into low Earth orbit.

That “eventually” is the problem and a solution.  If we can build and refuel spacecraft off-Earth, then we’ll be able to pump out cheap, truck-sized interplanetary spacecraft capable of moving a few tons of cargo anywhere in the solar system (if you’re patient).  On Earth there’s an engineering limit to how big you can build because of our ancient nemesis gravity, but once you’re building in space, size ceases to be a concern; we could build and efficiently slingshot entire cities around the solar system if we felt like it.  Building a huge launch vehicle to leave Earth, mine an asteroid, and return is a terrible way to get resources back to Earth.  Building thousands of cheap, tiny spacecraft on the Moon to travel to and from any of dozens of established mining colonies on 16-Psyche is also expensive, but much more efficient with much greater returns.  But manufacturing requires infrastructure, which means that a lot of what you recover in mining will be used to support the in-situ infrastructure that supports the mining.  And the people involved.  And their families.  And sooner or later (probably sooner) their legal issues.

Here’s a terrible metaphor.  If Henry VII (the king of England during the European realization of the New World) had wanted to mine gold in California, he would have had to fund a Lewis-and-Clark type expedition with all the necessary equipment and extra personnel to cross the continent, and put all of that onto a fleet of ships to get to the east coast.  It would have been a losing proposition.  But today, with plenty of intervening infrastructure, Elizabeth II could pack her corgis, trace out the same route as that hypothetical expedition on a boat, then a train, then a cab, buy a shovel when she arrives, and be in the gold business in no time.  It feels like building the United States is an inefficient way for English monarchs to mine gold, but keep in mind that mining gold isn’t entirely the point.  It turned out to be good for England (In retrospect.  Arguably.) in ways that they couldn’t possibly have predicted.

Expanding into space means creating new nations, new industries, and new places to go.  There are a lot of advantages to an essentially infinite supply of dirt-cheap resources and power.  More importantly, it means giving Earth a chance to lick its wounds and recover from what we’ve done so far.  We, as a species, have a hunger for energy and a taste for the rarer elements in the universe.  We’re not going to stop hunting for resources and building things, but we don’t have to do it here.

Asteroid mining isn’t about someone somewhere making trillions of dollars, although that will probably happen.  It’s not about advancing science, although that will definitely happen.  It’s about gaining access to the vast, vast majority of useful materials and fuel in the solar system, while making Earth-based mining and industry expensive and filthy by comparison.

Earth: a great place to live, but a terrible place to work.

Posted in -- By the Physicist, Astronomy, Engineering, Physics | 18 Comments