The original question was: … it confuses me that abstract concepts, such as Banach-Tarski, and other concepts in pure mathematics and theoretical physics, can be considered to have been “proven”. Is it not the case that one can only prove something by testing hypotheses in the real/physical world? And even then isn’t it a bit of a stretch to say that anything can really be proven beyond doubt?
Physicist: Hypothesis testing is the workhorse of scientific inquiry, used to determine whether or not a given effect is real. The result of a hypothesis test isn’t a proof or disproof, it’s an estimate of how likely it is that you would see a given result accidentally. The more unlikely it is that something would occur accidentally, the more likely it is to be a real effect. For example, we haven’t proven that the Higgs boson exists, it’s just that there’s only about a one in half a trillion chance that the data from CERN would be produced accidentally. That’s not a proof. Even so, if an effect works as predicted very consistently, then you may as well believe that it’s real.
Things are “proven” to be true with certainty in very much the same way that we can know with certainty that someone has won a chess game. There’s nothing etched into the fabric of the universe that determines how chess pieces move on a board (other than, you know, physically) or who won a given game, and yet everyone who knows the rules will be able to agree on the victor. Math, despite its vaunted status as the purest science and the means by which the reach of our simple minds can exceed their squishy grasp, is basically like the rules of chess or any other game.
Once the rules are established, you can prove things based on those rules and some logic (technically, logic is just more rules). For example, based on a reasonably short list of straightforward mathematical rules you can first define what a prime number is and then prove that there are an infinite number of them.
The rules in mathematics are called “axioms” and the results based on those rules are “theorems”. For example, “you can’t split a point in half” is an axiom while “there are an infinite number primes” is a theorem. When you first learn about numbers and arithmetic, you’re learning Peano’s axioms and lots of definitions and conclusions based on them. Like the rules of chess, axioms just establish what things you can and can’t do in math and people are free to argue about which they do or don’t want to include. Math doesn’t necessarily have anything to do with reality; it just happens to include some the most effective tools for understanding it ever conceived.
The fact that we can create new mathematics that doesn’t have anything to do with reality may seem like a weakness, but it’s turned out to be fantastically useful. For example, by generalizing the laws of geometry away from triangles, three dimensions of space, and even the very notion of distance, mathematicians paved the way for Einstein’s general relativity (which describes the nature of gravity in terms of warped spacetime). He basically just had to plug his new ideas about spacetime into math that had already been created.
Banach-Tarski is a century old result from set theory which says that you can (among other things) break a sphere into five or more sets, rotate and move those sets, and recombine them into two spheres identical to the first. These sets are less like block puzzles pieces and more like droplets in a fog, almost all of which are smaller than any given size. Notice that this is completely impossible physically. Lucky for Banach and Tarski, math isn’t dictated by the uptight strictures of reality.
XKCD: Funny because it’s true.
Banach-Tarski is based on the usual axioms of set theory, Zermelo–Fraenkel (ZF), but requires the addition of a hotly contested axiom, the “Axiom of Choice” (ZFC). “Hotly contested” in the math community is bit of a misnomer; mathematicians mostly just write long papers and stare angrily at each others shoes when they’re forced to shake hands. The axiom of choice is to mathematics as en passant is to chess; it comes up when it comes up, but you don’t need it in general (if you’ve ever made it through a game of chess and have no idea what en passant is: exactly).
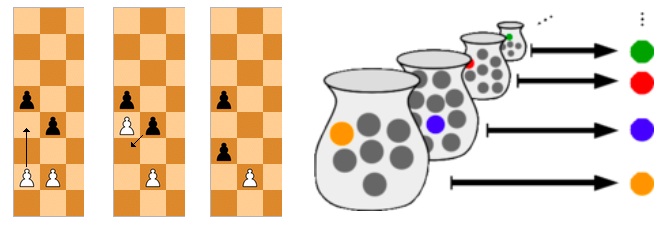
In abstract systems, the rules that are included are determined by preference, not physical reality. In order to be useful to more than one person, most of the rules are generally agreed upon, but some are not. (Left) En passant in chess and (Right) the axiom of choice in set theory.
The axiom of choice states that it is always possible to select (or even choose) a single item from each of a infinite collection of sets. This is easy if there are a finite number of sets (“just go ahead and do it”) or if there’s a nice rule you can come up with (“always pick the lowest number”). But sometimes you find yourself with an infinite set of infinite sets, none of which have a highest, lowest, or middlest point. If you’re wondering how you go about picking a single unique item out of each of these sets, the Axiom of Choice says “you just can, so be cool”. It is a completely made up statement that changes the rules of the game. It’s not a matter of true or false, it’s a matter of consistency and agreeing with other mathematicians.
Physics, despite being the queen of the sciences and the means by which we mortals may strive to understand the underlying nature of reality, isn’t any better than math. In physics you can “prove” that things are true or false, but only based on established rules: the “physical laws”. For example, Newton’s universal law of gravitation says that the force of attraction between two objects with masses M and m spaced a distance r apart is 
If those rules turn out to be false, then the proofs based upon them aren’t proofs. This is why physicists are so careful about establishing and verifying every detail of their theories. They spend (seemingly wasted) decades doing tests of things that they’re already almost 100% sure is right, because a flaw in any of the fundamental laws would ripple out into every “proved” thing that’s based on it.
Every now and again some base rule or assumption in math or physics is overturned. In math this is entirely due to logic, but physics is a bit more tricky. We can’t divine the rules of the universe with logic alone. If you were just a mind in a void, the nature of this universe would be a real shock. No matter how smart you are, you need experiment and observation to learn new things about the world.
It’s easy (well… fairly easy) to write down some physical laws that seem to describe what we know about the universe that turn out to be wrong. Without buckets of fantastically precise data and the math to understand it, there’s no way to know whether what you know is really only what you think. Newton’s laws are tremendously useful, but ultimately misinformed. They perfectly described the universe according to the data we had at the time; when more accurate (and more difficult to attain) data gave rise to “truer” physical theories we came to realize that Newtonian physics is merely a very good approximation.
Before Einstein we had safely assumed that time and space were completely independent. It took some seriously recondite phenomena (e.g., the invariance of the speed of light and a tiny error in Mercury’s orbit) to indicate that time and space are not some much related as they are different aspects of the same thing. Almost more sacred, before Bell we had assumed that everything exists in a single definite state, whether we know what that state is or not. This totally reasonable assumption is “realism”. Again, the difference between the universe we had assumed we lived in and the world we evidently do live in (probably) was a set of incredibly esoteric, nigh unnoticeable effects (e.g., the randomness of things like radioactive decay and the “impossible” statistics of entangled particles). It took a lot of clever experiments (dutifully checked, expounded upon, and multiply verified) and math to come to the conclusion that: nope, an assumption so fundamental that we call it “realism” or “the reality assumption” is actually false. Quantum physicists who have evolved beyond the need to be understood will call the property of definitely being in a single state “counterfactual definiteness“. Not that it’s worth mentioning, but if you can read this, you exist. Good on ya.
In mathematics you can prove things, but you’re ultimately just moving pieces around on a board. There’s a lot to learn and discover in the realms of logic, but math, like every abstract human endeavor, is all in our heads.
In physics you can prove things using physical laws. However, those physical laws are only true insofar as they always work perfectly (as far as we can measure and verify) in every scenario which, arguably, is the best you can hope for.
I assume there is some ‘ding-an-sich’ beneath it all, but can’t prove it…
Well stated, however, 2+2=4… unless Pi = 3 at a certain curvature of space-time. Not all is possible with physics, but all can be described by math. You and I can both be described as integrals, though it is impossible for us to write this out much less imagine. Naturally, this is where physics, and it’s convenient sidekick chemistry, describe this integral via DNA, protein chain folding, etc. to allow us insight into the grand scheme of things.
In closing, thanks again for the very well stated arguments. Let’s figure out a way to make the M in F=MA approach zero so we can get off this rock. Mirthful regards, Dan
You don’t need to be a mind in a void for the nature of the universe to be a real shock; the nature of the universe is demonstrably rather shocking for a mind in an ape too.
Lot’s of theorems (e.g., Pythagorean) are essential to physics. They can be proven from axioms, but whether those axioms are true or approximations that apply some places and times is an empirical questions that can’t be proved, but can be observed and thus are not provable. Absolute proofs are always conditional.
Some physics borders on provable. E.g., QED is based on basically geometrical properties of vectors and spinor fields. The masses and couplings of such vectors and spinors that exist does not follow from geometry and we are left with observations of electrons, muons,etc.
I see it this way… Math doesn’t prove things are real, but we have to transfer the “prove” to a mathematical equation so we can explain the results.
Please correct me if I am wrong.
There’s no 100% proof of anything, unless it depends on other ideas that have to be proved as well. Within interdependent sets of ideas, there can be 100% proof, but you can’t prove the whole set of ideas, as it then needs to be hooked to something outside it.
But there’s proof beyond reasonable doubt, and that’s what science deals with. That’s where we can make progress. And interestingly, conceptual physics, which has been enormously underestimated (because it did badly during the 20th century), is where it is most possible to make progress in that kind of way. It’s more possible than in mathematical physics, because there are similar sets of concepts described by the same mathematics, and also similar mathematics that gives similar numbers out, but which is in fact different. With concepts however, and in experimental physics, it’s really possible to get somewhere.
Only conditional statements are provable.