Physicist: The multiplication rules for signs are
You’d be hard pressed to find someone who disagrees with the first rule, and if you press hard you’ll find that almost everyone has been confused (at least once) by the third. In a nutshell, if you try to define the multiplication rules any other way, arithmetic stops working in a big hurry. Or at least, you have to scrap a lot of other math that’s incredibly useful.
When you multiply X by a positive integer Y you’re adding it to itself Y times. So it makes sense that a positive times a positive is positive. For example, 
Every time you multiply by a one-smaller-number, you take away another 3. Following the pattern, we take 3 away from zero and make a decent guess at how that pattern should continue:
Do this for a couple of different numbers and you can construct a multiplication table. Like this one!
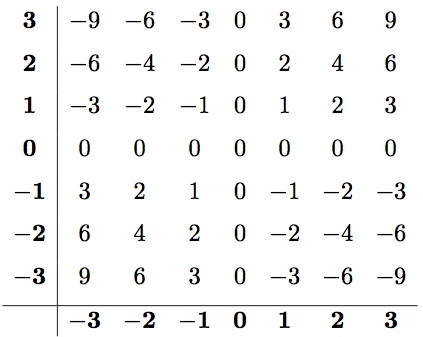
The times table for numbers between -3 and 3. Notice that the “2 row” always increases by 2 every step to the right (…, -2, 0, 2, 4, …). Notice that the “-3 row” always increases by -3 (which is to say, decreases by 3) every step to the right. While you’re noticing things, notice that the pattern is always the same for each row and column, even when the sign changes.
If the “negative times a negative” quadrant on the lower left were all negative instead of positive (e.g., “
So, “
In particular, the distributive property, which says that 
because “3” is defined as “3=1+1+1”. Losing the distributive property basically means you need to go home and start designing a new (and worse) kind of math from scratch.
For positive numbers there’s no issue, because (practically) everyone is fine with the “
But if you insist on using the rule “
And if you begrudgingly allow the “
On a case-by-case basis, it’s not obvious that a negative times a negative should be positive. But when you look at lots of examples and the number system overall, you find that the “
Using the wrong rules is a good, practical, and genuinely useful training in what not to do. It’s well worth your time to shake off the shackles of mundanity and conformity, so that you can forge into a world of new discoveries. Specifically, you’ll discover why arithmetic’s shackles are usually left unshaken.
I find it best to just follow the rules; when I start delving deeper my eyes get crossed and smoke comes out of my ears; but that’s just me ….
Klaatu – if you recall, we had this discussion months ago; and to be honest, I’m still confused – but this helps me get part-way; thank you
As a junior high teacher I used to explain it this way: The Negative Sign means turn around.
__-6___-5___-4___-3___-2___-1___0___1___2___3___4___5___6__
Start at 0. 3 means go to the right 3. -3 means go to the left 3. In multiplication “-” still means turn around.
-(2)*(3) = -6 or (-2)*(3) = -(2)*(3) = -6 One negative – turn around once.
(-2)*(-3) = +6 Two negatives – turn around twice.
If all else fails, and od number of negative signs = negative. An even number = positive
What a nice simply-explained answer. Thanks!
This is the kind of area where looking at the theory of permutation can be useful. Multiplication is really just a specialized form of addition and so ‘multiplication’ is really just ‘multiple addition’.
If you are multiplying by zero you end up with zero copies of the original number which of course adds up to zero.
Extending this a negative multiplication becomes a negative multiple addition. A negative addition is simply a subtraction so the permutation here becomes a ‘multiple subtraction’.
(+n) . (+m) = (+a), (+n) . (-m) = (-a), (-n) . (-m) = (+a).
(+4) . (+3) = 0+4+4+4 = (+12), (+4) . (-3) = 0-4-4-4 = (-12)
Don’t get confused by division though. Although division is the inverse of multiplication it is not quite the same procedure. – Direct division is generally actually incomputable using simple operators.
Instead division by permutation uses an indirect iterative process using multiple addition and manipulation of the denominator to create a temporary token value which is then compared and adjusted repeatedly until it adequately fits to the value of the nominator..
If that sounds complicated it is. 🙂
However division for negative numbers uses exactly the same rules as for multiplication of negative numbers. If either operand is negative then the result is negative, if both are negative then the result is positive.
let’s keep going; now you’ve got me looking up ‘imaginary’ numbers; so, the ‘imaginary’ part is ‘i’; ‘i’ is the square root of -1; the sq root of – 1 is (-1 x -1), I think ; -1 x-1 = 1; what’s the point !! what am I missing? – where did I go wrong?
@sokor
The square roots of 4 are 2 and -2, since 22=4 and (-2)2=4. The square roots of 1 are 1 and -1, since 12=1 and (-1)2=1. Finally, since i is defined using i2=-1, the square roots of -1 are i and -i.
Ah, you people are making this to complicated.
If I owe three people five dollars each that makes me 3* -5 = -15 dollars poor.
If I kill them then I’m -3*-5 = 15 dollars richer.
The easiest way to tell people that – * – = + is that this follows as a logical consequence of the axioms of the set theory. In the set theory, one first postulates the existence of some objects that are called sets and lays out the statements/axioms that describe some properties of the objects without a proof. Then, one starts deriving logical consequences – theorems. Now, one of the axioms says that there exists at least one infinite set that is inductive (this property is needed to DEFINE what a natural number is). Yes, numbers are sets. All of them. That’s because in maths EVERYTHING is a set. So, once the natural numbers have been defined, one proceeds to define what a whole number is. One also defines the 2 basic operations: addition and multiplication. First for the natural numbers and then – by extension – for the whole numbers. And this is the moment when you can SEE WITH YOUR OWN EYES that from the very basic and undeniable rules the rule for the multiplication arises. So, the sign rules are INEVITABLE consequences of the axiomss of the set theory.
Why is light moved maximum speed?
Aside from the rules of arithmetic requiring a negative times a negative to yield a positive, in the real, physical world a negative times a negative is a positive. Let’s look at a company’s accounting books. The numbers represent real things, people with accounts and money that these people are paying or receiving. The products are cash flows in and out of the company – also quite real.
Suppose I own the company. Cash that is paid to me is a positive cash flow (I get more $), and cash that I pay out is a negative cash flow (I have fewer $). Suppose that accounts that I add to my portfolio are positive (more accounts), and accounts that I remove from my portfolio are negative (fewer accounts).
Let’s see what the effect on my cash flow is as I add and remove multiple accounts all of which either pay me the same amount of money or that I pay the same amount of money to.
If I add 5 accounts each of which pays me $7 per month, then I have increased my cash flow: (+5)(+$7) = +$35 per month.
If I add 3 accounts each of which requires me to pay out $2 per month, then I have a reduced my cash flow: (+3)(-$2) = -$6 per month.
If I remove 4 accounts each of which paid me $12 per month, then I have reduced my cash flow: (-4)(+$12) = -$48 per month.
Finally, if I remove 6 accounts each of which I paid $9 per month, then I have increased my cash flow: (-6)(-$9) = +$56 per month.
In this last case, my cash flow is increased because I have stopped paying money out.
Suppose I have 7 accounts that each pay me $10. I have 7 x $10 = $70 of cash flowing in.
Suppose, instead, I have 11 accounts each of which I pay $6. That means I will have 11 x $6
The last two sentences of this post should be deleted. They are left-overs from an earlier draft. I did not see them below the bottom of the window when I posted. But I do not see how to edit the post.
Let us start from the most beautiful equation
e^ιπ+1=0.
This gives
e^ιπ=-1.
Now, taking multiplication
(-1)(-1)=e^ιπ e^ιπ.
This implies
(-1)(-1)=cos 2π+ ι sin 2π= +1.
In the same way, one can show that
(-a)(-a)=a^2
This proves that “negative” multiplied with “negative” is “positive”
Unit analysis helps for some students, too. When I measure a rectangle from one corner, say it’s 2 cm by 3cm, I might multiply the sides to find the area, but I don’t get 6 cm. Rather, I get 6 *square* cm, because I have to multiply the units, too. Centimeters times centimeters is centimeters-squared. Not a distance; an area.
If I measure the rectangle in a negative plane (or measure it from the diagonally opposing corner) I might measure -3 cm by -2 cm. But area can’t be negative, the rectangle still has an area of 6 cm^2.
My original post would have made much more sense if Quora hadn’t removed the formatting from my math.. Here it is separated out into separate lines..
(+n) . (+m) = (+a),
(+n) . (-m) = (-a),
(-n) . (-m) = (+a).
(+4) . (+3) = 0 + 4 + 4 + 4 = (+12),
(+4) . (-3) = 0 – 4 – 4 – 4 = (-12).
But that physical argument fails when extended to 3 dimensions. -2 cm x -3 cm x -4 cm should be a volume of 24 cubic cm, but while the neg x neg = pos gives an area of 6 sq cm for one side, the volume is still calculated as -24 cu cm.
Oh, good point! Feeling a little sheepish now…
No need to feel sheepish. We’ve all been there.