Q: How do we know that π never repeats? If we find enough digits, isn’t it possible that it will eventually start repeating?

Posted on December 20, 2013 by The Physicist

Physicist: In physical sciences we catalog information gained through observation (“what’s that?”), then a model is created (“I bet it works like this!”), and then we try to disprove that model by using experiments (“if we’re right, then we should see this weird thing happening”).  In the physical sciences the aim is to disprove, because proofs are always out of reach.  There’s always the possibility that you’re missing something (it’s a big, complicated universe after all).

Mathematics is completely different.  In math (and really, only in math) we have the power to prove things.  The fact that π never repeats isn’t something that we’ve observed, and it’s not something that’s merely “likely” given that we’ve never observed a repeating pattern in the first several trillion digits we’ve seen so far.

The digits of pi never repeat because it can be proven that π is an irrational number and irrational numbers don’t repeat forever.

If you write out the decimal expansion of any irrational number (not just π) you’ll find that it never repeats.  There’s nothing particularly special about π in that respect.  So, proving that π never repeats is just a matter of proving that it can’t be a rational number.  Rather than talking vaguely about math, the rest of this post will be a little more direct than the casual reader might normally appreciate.  For those of you who just scrolled down the page and threw up a little, here’s a very short argument (not a proof):

It turns out that \pi = 4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots\right).  But this string of numbers includes all of the prime numbers (other than 2) in the denominator, and since there are an infinite number of primes, there should be no common denominator.  That means that π is irrational, and that means that π never repeats.  The difference between an “argument” and a “proof” is that a proof ends debates, whereas an argument just puts folk more at ease (mathematically speaking).  The math-blizzard below is a genuine proof.  First,

Numbers with repeating decimal expansions are always rational.

If a number can be written as the D digit number “N” repeating forever, then it can be expressed as N\times 10^{-D} + N\times 10^{-2D} + N\times 10^{-3D}+\cdots.  For example, when N=123 and D=3:

\begin{array}{ll}0.123123123123123\cdots\\=0.123+0.000123+0.000000123+\cdots\\=123\times 10^{-3} + 123\times 10^{-6} + 123\times 10^{-9}+\cdots\end{array}

Luckily, this can always be figured out exactly using some very old math tricks.  This is just a geometric series, and N\times 10^{-D} + N\times 10^{-2D} + N\times 10^{-3D}+\cdots = N\frac{10^{-D}}{1-10^{-D}} = N\frac{1}{10^{D}-1}.  So for example, 0.123123123123123 = 123\frac{1}{10^3-1} = \frac{123}{999}=\frac{41}{333}.

Even if the decimal starts out a little funny, and then settles down into a pattern, it doesn’t make any difference.  The “funny part” can be treated as a separate rational number.  For example, 5.412123123123123\cdots = 5.289 + 0.123123\cdots = \frac{5289}{1000} + \frac{41}{333}.  And the sum of any rational numbers is always a rational number, so for example, \frac{5289}{1000} + \frac{41}{333} = \frac{5289\cdot333 + 41\cdot1000}{1000\cdot333} = \frac{1802237}{333000}.

So, if something has a forever-repeating decimal expansion, then it is a rational number.  Equivalently, if something is an irrational number, then it does not have a repeating decimal.  For example,

√2 is an irrational number

So, in order to prove that a number doesn’t repeat forever, you need to prove that it is irrational.  A number is irrational if it cannot be expressed in the form \frac{A}{B}, where A and B are integers.  √2 was the first number shown conclusively to be irrational (about 2500 years ago).  The proof of the irrationality of π is a little tricky, so this part is just to convey the flavor of one of these proofs-of-irrationality.

Assume that \sqrt{2} = \frac{A}{B}, and that A and B have no common factors.  Then it follows that 2B^2 = A^2.  Therefore, A is an even number since A^2 has a factor of 2.  But if \frac{A}{2} is an integer, then we can write: 2B^2 = 4\left(\frac{A}{2}\right)^2 and therefore B^2 = 2\left(\frac{A}{2}\right)^2.  But that means that B is an even number.

This is a contradiction, since we assumed that A and B have no common factors.  By the way, if they did have common factors, then we could cancel them out.  No biggie.

So, √2 is irrational, and therefore its decimal expansion (√2=1.4142135623730950488016887242096980785696…) never repeats.  This isn’t just some experimental observation, it’s an absolute fact.  That’s why it’s useful to prove, rather than just observe, that

π is an irrational number

The earliest known proof of this was written in 1761.  However, what follows is a much simpler proof written in 1946.  Unfortunately, there don’t seem to be any simple, no-calculus proofs floating around, so if you don’t dig calculus and some of the notation from calculus, then you won’t dig this.  Here goes:

Assume that \pi = \frac{a}{b}.  Now define a function f(x) = \frac{x^n(a-bx)^n}{n!}, where n is some positive integer, and that excited n, n!, is “n factorial“.  No problems so far.

All of the derivatives of f(x) taken at x=0 are integers.  This is because f(x) = \frac{x^n(a-bx)^n}{n!} = \sum_{j=0}^n \frac{a^{n-j}(-b)^j}{n!} x^{n+j} (by the binomial expansion theorem), which means that the kth derivative is f^{(k)}(x) = \sum_{j=0}^n \frac{n!}{j!(n-j)!}\frac{a^{n-j}(-b)^j}{n!}(n+j)(n+j-1)\cdots(n+j-k+1) x^{n+j-k} = \sum_{j=0}^n \frac{n!}{j!(n-j)!}\frac{a^{n-j}(-b)^j}{n!}\frac{(n+j)!}{(n+j-k)!} x^{n+j-k} = \sum_{j=0}^n a^{n-j}(-b)^j\frac{(n+j)!}{j!(n-j)!(n+j-k)!} x^{n+j-k}

If k<n, then there is no constant term (an x0 term), so f^{(k)}(0) =0.  If n≤k≤2n, then there is a constant term, but f^{(k)}(0) is still an integer.  The j=k-n term is the constant term, so:

\begin{array}{ll}f^{(k)}(0)=\sum_{j=0}^n a^{n-j}(-b)^j\frac{(n+j)!}{j!(n-j)!(n+j-k)!} 0^{n+j-k}\\[2mm]=a^{2n-k}(-b)^{k-n}\frac{k!}{(k-n)!(2n-k)!0!}\\[2mm]=a^{2n-k}(-b)^{k-n}\frac{k!}{(k-n)!(2n-k)!}\end{array}

a and b are integers already, so their powers are still integers.  \frac{k!}{(k-n)!(2n-k)!} is also an integer since \frac{k!}{(k-n)!(2n-k)!}=\frac{k!}{(k-n)!n!}\frac{n!}{(2n-k)!} = {k \choose n}\frac{n!}{(2n-k)!}.  “k choose n” is always an integer, and \frac{n!}{(2n-k)!} = n(n-1)(n-2)\cdots(2n-k+1), which is just a string of integers multiplied together.

So, the derivatives at zero, f^{(k)}(0), are all integers.  More than that, by symmetry, f^{(k)}(\pi), are all integers.  This is because

\begin{array}{ll}f(\pi-x)=f\left(\frac{a}{b}-x\right)\\[2mm]=\frac{\left(\frac{a}{b}-x\right)^n(a-b\left(\frac{a}{b}-x\right))^n}{n!}\\[2mm]=\frac{\left(\frac{a}{b}-x\right)^n(a-\left(a-bx\right))^n}{n!}\\[2mm]=\frac{\left(\frac{a}{b}-x\right)^n(bx)^n}{n!}\\[2mm]=\frac{\left(\frac{1}{b}\right)^n\left(a-bx\right)^n(bx)^n}{n!}\\[2mm]=\frac{\left(a-bx\right)^n x^n}{n!}\end{array}

This is the same function, so the arguments about the derivatives at x=0 being integers also apply to x=π.  Keep in mind that it is still being assumed that \pi=\frac{a}{b}.

Finally, for k>2n, f^{(k)}(x)=0, because f(x) is a 2n-degree polynomial (so 2n or more derivatives leaves 0).

After all that, now construct a new function, g(x) = f(x)-f^{(2)}(x)+f^{(4)}(x)-\cdots+(-1)^nf^{(2n)}(x).  Notice that g(0) and g(π) are sums of integers, so they are also integers.  Using the usual product rule, and the derivative of sines and cosines, it follows that

\begin{array}{ll}\frac{d}{dx}\left[g^\prime(x)sin(x) - g(x)cos(x)\right]\\[2mm] = g^{(2)}(x)sin(x)+g^\prime(x)cos(x) - g^{\prime}(x)cos(x)+g(x)sin(x)\\[2mm] =sin(x)\left[g(x)+g^{(2)}(x)\right]\\[2mm] =sin(x)\left[\left(f(x)-f^{(2)}(x)+f^{(4)}(x)-\cdots+(-1)^nf^{(2n)}(x)\right)+\left(f^{(2)}(x)-f^{(4)}(x)+f^{(6)}(x)-\cdots+(-1)^nf^{(2n+2)}(x)\right)\right]\\[2mm] =sin(x)\left[f(x)+\left(f^{(2)}(x)-f^{(2)}(x)\right)+\left(f^{(4)}(x)-f^{(4)}(x)\right)+\cdots+(-1)^n\left(f^{(2n)}(x)-f^{(2n)}(x)\right)+(-1)^nf^{(2n+2)}(x)\right]\\[2mm] =sin(x)\left[f(x)+(-1)^nf^{(2n+2)}(x)\right]\\[2mm] =sin(x)f(x) \end{array}

f(x) is positive between 0 and π, since (a-bx)^n>0 when 0<x<\frac{a}{b}=\pi.  Since sin(x)>0 when 0<x<π as well, it follows that 0<\int_0^\pi f(x)sin(x)\,dx.  Finally, using the fundamental theorem of calculus,

\begin{array}{ll}\int_0^\pi f(x)sin(x)\,dx\\[2mm]= \int_0^\pi \frac{d}{dx}\left[g^\prime(x)sin(x) - g(x)cos(x)\right]\,dx\\[2mm]= \left(g^\prime(\pi)sin(\pi) - g(\pi)cos(\pi)\right) - \left(g^\prime(0)sin(0) - g(0)cos(0)\right)\\[2mm]= \left(g^\prime(\pi)(0) - g(\pi)(-1)\right) - \left(g^\prime(0)(0) - g(0)(1)\right)\\[2mm] = g(\pi)+g(0)\end{array}

But this is an integer, and since f(x)sin(x)>0, this integer is at least 1.  Therefore, \int_0^\pi f(x)sin(x)\,dx>1.

But check this out: if 0<x<\pi=\frac{a}{b}, then sin(x)f(x)=sin(x)\frac{x^n(a-bx)^n}{n!}\le\frac{x^n(a-bx)^n}{n!}\le\frac{\pi^n(a-bx)^n}{n!}\le\frac{\pi^na^n}{n!}.

Therefore, \int_0^\pi f(x)sin(x)\,dx<\int_0^\pi \frac{\pi^na^n}{n!}\,dx=\frac{\pi^{n+1}a^n}{n!}.  But here’s the thing; we can choose n to be any positive integer we’d like.  Each one creates a slightly different version of f(x), but everything up to this point works the same for each of them.  While the numerator, π(πa)n, grows exponentially fast, the denominator, n!, grows much much faster for large values of n.  This is because each time n increases by one, the numerator is multiplied by πa (which is always the same), but the denominator is multiplied by n (which keeps getting bigger).  Therefore, for a large enough value of n we can always force this integral to be smaller and smaller.  In particular, for n large enough, \int_0^\pi f(x)sin(x)\,dx<\frac{\pi^{n+1}a^n}{n!}<1.  Keep in mind that a is assumed to be some definite number, so it can’t “race against n”, which means that this fraction always becomes smaller and smaller.

Last step!  We can now say that if π can be written as \pi =\frac{a}{b}, then a function, f(x), can be constructed such that \int_0^\pi f(x)sin(x)\,dx\ge 1 and \int_0^\pi f(x)sin(x)\,dx<1.  But that’s a contradiction.  Therefore, π cannot be written as the ratio of two integers, so it must be irrational, and irrational numbers have non-repeating decimal expansions.

Boom.  That’s a proof.

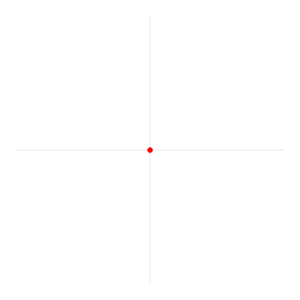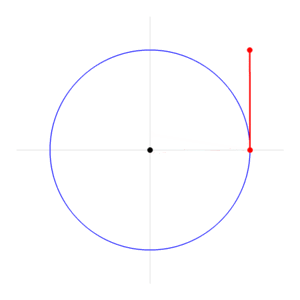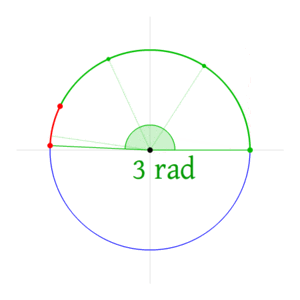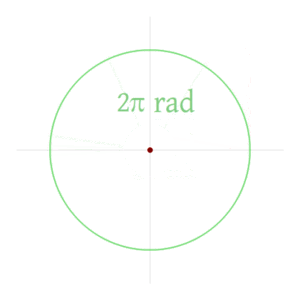
For those of you still reading, it may occur to you to ask “wait… where did the properties of π get into that at all?”.  The proof required that sine and cosine be derivatives of each other, and that’s only true when using radians.  For example, \frac{d}{dx}sin(x) = \frac{\pi}{180}cos(x) when x is in degrees.  So, the proof requires that \frac{d}{dx}sin(x) = cos(x), and that requires that the angle is given in radians.  Radians are defined geometrically so that the angle is described by the length of the arc it traces out, divided by the radius.  Incidentally, this definition is equivalent to declaring the small angle approximation: sin(x)\approx x.

The radian.

The radian.

This defines the angle of a full circle as 2π radians and as a result of geometry and the definitions of sine and cosine, sin(π radians) = 0, cos(π radians) = -1, \frac{d}{dx}sin(x) = cos(x), and that’s enough for the proof!

Subtle, but behind all of that algebra, is a bedrock of geometry.

This entry was posted in -- By the Physicist, Geometry, Logic, Math. Bookmark the permalink.

40 Responses to Q: How do we know that π never repeats? If we find enough digits, isn’t it possible that it will eventually start repeating?

  1. Manny says:
    December 20, 2013 at 2:49 pm

    My math is rusty, but at least I know where to go if someone asks me why pi is irrational. I never thought that the decimals really never generate a repeating sequence whatsoever.

    Thanks for the explanation. I may need to start learning calculus again. 😀

  2. The Cool Dude says:
    December 20, 2013 at 3:39 pm

    On the “Last Step” when pointing out the contradiction you accidentally used the same inequality twice, rather than two different ones.

  3. Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:
    December 20, 2013 at 6:43 pm

    Fixed!

  4. mORA says:
    December 21, 2013 at 3:52 am

    Formula in some paraghaphs are distorted

  5. Pingback: How do we know that π never repeats? | eDue

  6. The Spleen says:
    December 21, 2013 at 6:39 am

    Hi, two tiny errors (I think):
    When you introduce the binomial expansion, you forgot the bionomial coefficient in the very first equation.
    Also in the end of this paragraph: “But this is an integer, and since f(x)sin(x)>0, this integer is at least 1. Therefore, […]”, you write >1 instead of ≥1.

    Thanks for the wonderful proof! 🙂

  7. Ben says:
    December 21, 2013 at 12:02 pm

    What are the odds you can show us the proof that π isn’t algebraic?

  8. Flavian Popa says:
    December 23, 2013 at 4:41 am

    Excellent post, I love how you explain and make things clear, both from a simple and a more complex mathematical framework! Happy Christmas and Holidays!

  9. Doyle says:
    March 4, 2014 at 5:57 pm

    I had no idea 9 was a prime number (fifth paragraph).

  10. Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:
    March 4, 2014 at 6:02 pm

    It isn’t. But the sum includes all odd numbers, which includes (as a subset) all primes other than 2.

  11. Doyle says:
    March 4, 2014 at 6:13 pm

    Oh, you are right. I ignored the word”includes” the first time I read it. Thanks!

  12. Anthony says:
    April 2, 2014 at 10:33 am

    Would that be tau radians?

  13. Adam says:
    November 2, 2014 at 1:58 am

    Pfft, I’m not reading all of that. To answer the title though, you can just say “we know that pi never repeats, because if it repeats, then it isn’t pi.”

  14. Rich says:
    March 21, 2015 at 6:17 pm

    So, is it impossible to generate the decimal points of π without using calculus? Or are there two numbers one can divide to generate it?

  15. Crimsonbat83 says:
    March 28, 2015 at 3:56 am

    @Rich – Sure! Divide pi^2 by pi, and there you have it! 😀

  16. Jack says:
    May 12, 2015 at 9:13 pm

    There are only a limited number of permutations of 9 digits, so pi has to repeat at some point.

  17. Aieou says:
    May 22, 2015 at 11:58 pm

    @Rich “Irrational” means that no, you cannot divide two “ordinary” (i.e. rational) numbers together to get π, by definition. However, it is most certainly possible to generate digits of π without calculus. There are methods such as Buffon’s Needle (http://mste.illinois.edu/activity/buffon/) or what the Greeks did to try and find it out with geometry.

  18. WillL says:
    September 20, 2015 at 2:22 am

    @Jack: A limited number of permutations assumes a finite number of positions for those digits to be placed in, which is not true of an irrational number. Consider 1415 and 1415926; if they occurred in different places in pi, you would say that it repeated (1415), but those are two separate permutations of different length and thus can’t be compared for repetition. Since pi is an irrational number of infinite length, it can have permutations of infinite length, and therefore can never repeat.

  19. Mark Johnson says:
    October 23, 2015 at 11:41 pm

    I know others (i.e. Japanese) computed pi to more than 100 million decimal places with supercomputers and found no pattern let alone a repeating pattern. Others have computed it beyond these digits since; aren’t we a curious bunch and with time on our hands? It is truly a remarkable number. The question I have is whether pi can be expressed with a repeatable pattern in a base other than 10.

  20. Jack says:
    October 28, 2015 at 12:36 am

    @WillL: Oh that makes sense, thanks

  21. Zach says:
    October 28, 2015 at 9:22 pm

    @Mark Johnson – if you express it in base pi, then it’s represented by 10, which is nice pattern of sorts.

  22. s says:
    October 31, 2016 at 2:53 pm

    how do we know that it doesn’t repeat, when we can’t see the whole entire number written out?

  23. Aaron says:
    December 22, 2016 at 5:12 pm

    Are there an infinite number of irrational numbers?

  25. Pingback: Q: How accurately do we need to know π? Is there a reason to know it out to billions of digits? | Ask a Mathematician / Ask a Physicist

  26. Richard says:
    November 16, 2017 at 8:24 am

    Really big reply , but this reply doesn’t deal with the method of calculation of Pi and its problematic … The undeniable fact is that the value which we use for Pi is actually not calculated by definition for Pi … We just associate the value we calculated to this definition … Another undeniable fact is that the most fundamental formulas like C=2Pi*r and A= Pi*r^2 have never been proven … We don’t know what curve really is , we don’t have any prior definition for lengths of curves etc … Number Pi as we use it today is nothing more than mathematical concept ,which has nothing to do with reality … By Archimedes method you never ever can reach the end ,,, and all the rest of those formulas for calculating Pi , they are nothing more than number generators , which make Archimedes-Pythagoras method more efficient and faster , that’s it… Non of those formulas explaining what curve is. Equating number Pi with square root of two is nobrainer ..there are major differences .. square root of two is solving straight line + we can grab square root of 2 into compass …

  27. Aaron says:
    November 16, 2017 at 1:13 pm

    So, since Pi is irrational, and used in calculating the area of a circle, does that mean we can never calculate the exact area of a circle? Does a circle never truly have an exact area, only an approximate area?

  28. Jack M says:
    August 13, 2018 at 2:51 am

    @Dick: As long as we can count (exist, think, grow, etc), numbers will not have an end. There lies the “living proof” of irrational and infinite numbers.

    Pi also has much reality…it may even prove it; that even within the confines of a circle there is infinite change, so long as curve exists. And a curve is our ability to change direction. You may do the same thing over and over but will never fail to think new thoughts or combinations of…I would be as bold as to say that irrational numbers prove our existence is not temporal and certainly not finite.

  29. Jack M says:
    August 13, 2018 at 2:54 am

    Thanks Physicist, for a rich and rewarding article.

  30. Pingback: Q: How was the number π first discovered? How did we first figure out it was 3.14…? | Ask a Mathematician / Ask a Physicist

  31. Hal says:
    November 16, 2018 at 1:09 pm

    Thanks Physicist,
    Don’t apologize for complication if it is the simplest approach.
    If someone can’t follow why pi is irrational, let them eat cake.
    Cheers

  32. wernher von Burg Falkenberg says:
    April 2, 2019 at 10:00 am

    I have a better Way ???

  33. Robbie says:
    October 4, 2019 at 10:49 am

    1) Irrational numbers never repeat, 2) Pi is irrational, 3) Therefore, pi never repeats.
    1) Any number that doesn’t repeat is irrational, 2) Pi never repeats, 3) Therefore, pi is irrational.
    Something seems circular to me in this article but I ain’t no mathematician! I think unless we count all the way until infinity we may never know?

  34. Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:
    October 5, 2019 at 11:30 am

    @Robbie
    What I was trying to get across is that “a number is rational if and only if it (eventually) repeats forever”. Basically there are two categories for numbers: they’re either rational and repeat, or they’re irrational and don’t repeat. Then it’s a matter of showing (not easily) that pi falls into the irrational category.

  35. Alexander says:
    January 23, 2020 at 9:50 pm

    I have an easier way to put it.

    Because circles are infinite, pi is infinite.

  36. Owen says:
    January 23, 2020 at 10:01 pm

    This was really helpful! Thanks a lot!

  37. David says:
    July 28, 2020 at 1:02 pm

    I’m sure it is proved that pi is an irrational number, and you may well be able to prove that irrational numbers never repeat. But I’m interested in the second of those, and if it’s above I haven’t seen it. I’ve seen:

    “If you write out the decimal expansion of any irrational number (not just π) you’ll find that it never repeats.”

    That isn’t a proof. I’m not saying there isn’t one, but if there is, that ain’t it.

  38. JustNaCl says:
    May 17, 2021 at 9:49 am

    The definition of an “irrational” number is one that is not equal to one integer divided by another integer. Only rational numbers, those that can be written as the ratio of two integers, repeat their decimal expansions (or their expansion in any integer base).

    So by proving that pi is not rational (not equal to an integer ratio) the article proves that it does not repeat.

  39. Pingback: CANTOR #3: Math is Freedom – Math Renaissance

  40. jeff says:
    August 16, 2023 at 2:14 pm

    Seems probable that ‘substrings’ of it could repeat in various ways. For example, ‘1415’ could appear somewhere further on, just as a coincidence. In fact, with an infinite string of digits, you could probably find ‘1415’ an infinite number of times, couldn’t you? And then say the same about ‘1415926’, and in fact about any such string? A lot of weird stuff can happen in the Infinite Hotel.

Leave a Reply

Your email address will not be published.