Q: In the NEC “faster than light” experiment, did they really make something go faster than light?

The original question was: I was reading an article by Lijun Wang the experiment I think is called the NEC experiment.  Basically what the guy does is speed up light so that it goes faster than the than the speed of light.  If anything goes faster than light does that mean it goes backwards in time?  Is this experiment genuine?

Here’s a description of the experiment.

Physicist: This experiment showed up in the popular media about ten years ago, and it’s still bothering people today.  The very short answer is: nope!  No physical object ever travels faster than light, and yet the experiment is real. This is pretty tricky, but it comes down to a distinction between “phase velocity” (light speed, “c”) and “group velocity” (depends on the medium).  The experiment essentially requires a “standing wave” in the test chamber, with waves at many frequencies. These light waves interact in such a way that they create peaks, like when you pluck two slightly-out-of-tune guitar strings and you hear a pulsing sound.  These peaks are usually called “wave groups” or “wave packets”.  The peaks move around, and you can more or less keep track of where they are (more exactly; you can infer where they were after the fact). The pivotal point is that the experiment isn’t about turning on some kind of laser, that sends out a pulse, that suddenly moves faster than light.  The experiment is about peaks made out of standing waves, and the standing waves are already all over the inside of the test chamber when the experiment begins. In the middle of the camber is a specially constructed cloud with extremely weird and strong optical properties, that changes how fast light of various frequencies move through it (slowing only, but to various degrees).  Specifically, the lower the frequency, the slower it’s allowed to propagate through the cloud.  This is a weird set up, and it’s difficult to produce.

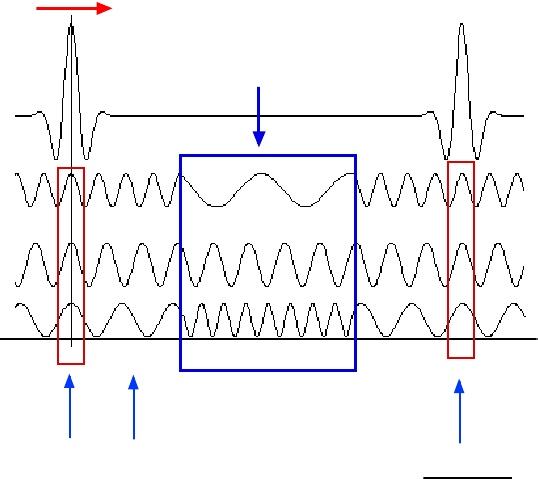
Waves of different frequencies travel at different speeds and that gives rise to "groups" or "wave packets". The red boxes are examples of how waves of different frequencies can add up. The blue box shows what happens to various waves as they pass through the cloud.

The above image was jacked from the original author’s follow up explanatory paper. A good estimate for the group velocity in general is , where is the angular frequency and k is the wave number.  The take home message from this is; by creating a material that has a very strong relationship between and k you can dial up the group velocity to ridiculous levels (in this case -310c).  For comparison, the group velocity of light in water differs from the phase velocity by less than 1% (which is different from 31,000%). So, by changing how the different frequencies move through the cloud you change how the peaks move around (making them faster than light in this case), however nothing is actually moving faster than light, just a non-information-carrying effect. A much simpler example of this sort of thing is the “scissor paradox”.  Although the execution is different, the underlying idea is exactly the same. When you close a pair of scissors the point where the blades intersect is moving much faster than either blade, and if you were to construct a pair of scissors large and fast enough, then the point of intersection could easily move faster than light, but it wouldn’t be able to carry any kind of information (in part) because you’d already see the slower-than-light blades moving long before the intersection point got to you.  Also, it’s not like you can mail a letter by attaching it to an intersection.  An intersection isn’t an actual “thing”.

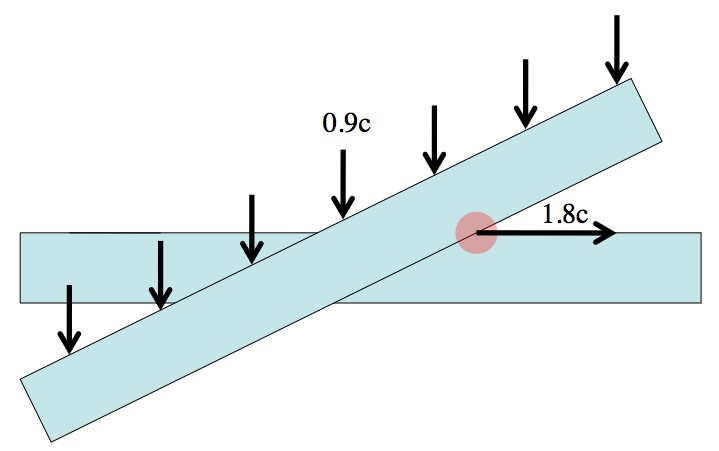
Nothing can physically move faster than light. However, abstract points, like the point of intersection or even the peak of a wave packet, can move as fast as they want.

This NEC thing is a similar “paradox”.  And again, the author was kind enough to explain this whole thing here. To answer the follow up, “does going faster than light mean you go back in time?”: maybe.  Probably.  But, it’s never come up.