Q: Why is pi not a definite number?

The original question was: If the diameter of a circle is a fixed number, say 10cm, why does Pi go on for billions of numbers even though it extrapolates from the diameter’s value? Why is it not a definite number?

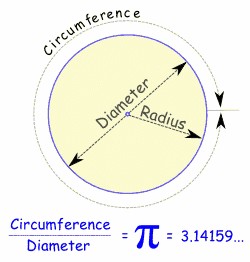
Mathematician: Basically, a diameter of 10cm leads to a circumference that is an irrational number. There is a very simple relationship between diameter and circumference, given by circumference = $\pi\times$ diameter. It just so happens that the proportionality constant is an irrational number, which means that it has no [finite length] patterns in its digits that repeat forever. This occurs because, well, that is a property that circles have. $\pi$ is however a “definite” number, in the sense that it is a single fixed number that is well defined. It’s just that since its digits don’t have a single pattern, there is no way to write them out nicely. Note that when you write 10 this is the same thing as 10.00000000000000…. with an infinite number of zeros. We can write this just as 10 because it’s understood that this implies that all other digits after the decimal point are 0. So, it’s not that 10 doesn’t have an infinite number of digits (like $\pi$ ), it’s just that those digits are zero (unlike $\pi$ ) which makes it easy to come up with a notation for ten (namely, 10).