Clever student:
I know!
=
=
=
=
.
Now we just plug in x=0, and we see that zero to the zero is one!
Cleverer student:
No, you’re wrong! You’re not allowed to divide by zero, which you did in the last step. This is how to do it:
=
=
=
=
which is true since anything times 0 is 0. That means that
=
.
Cleverest student :
That doesn’t work either, because if then
is
so your third step also involves dividing by zero which isn’t allowed! Instead, we can think about the function and see what happens as x>0 gets small. We have:
=
=
=
=
=
=
=
=
=
So, since = 1, that means that
= 1.
High School Teacher:
Showing that approaches 1 as the positive value x gets arbitrarily close to zero does not prove that
. The variable x having a value close to zero is different than it having a value of exactly zero. It turns out that
is undefined.
does not have a value.
Calculus Teacher:
For all , we have
.
Hence,
That is, as x gets arbitrarily close to (but remains positive),
stays at
.
On the other hand, for real numbers y such that , we have that
.
Hence,
That is, as y gets arbitrarily close to ,
stays at
.
Therefore, we see that the function has a discontinuity at the point
. In particular, when we approach (0,0) along the line with x=0 we get
but when we approach (0,0) along the line segment with y=0 and x>0 we get
.
Therefore, the value of is going to depend on the direction that we take the limit. This means that there is no way to define
that will make the function
continuous at the point
.
Mathematician: Zero raised to the zero power is one. Why? Because mathematicians said so. No really, it’s true.
Let’s consider the problem of defining the function for positive integers y and x. There are a number of definitions that all give identical results. For example, one idea is to use for our definition:
:=
where the y is repeated x times. In that case, when x is one, the y is repeated just one time, so we get
=
.
However, this definition extends quite naturally from the positive integers to the non-negative integers, so that when x is zero, y is repeated zero times, giving
=
which holds for any y. Hence, when y is zero, we have
.
Look, we’ve just proved that ! But this is only for one possible definition of
. What if we used another definition? For example, suppose that we decide to define
as
:=
.
In words, that means that the value of is whatever
approaches as the real number z gets smaller and smaller approaching the value x arbitrarily closely.
[Clarification: a reader asked how it is possible that we can use in our definition of
, which seems to be recursive. The reason it is okay is because we are working here only with
, and everyone agrees about what
equals in this case. Essentially, we are using the known cases to construct a function that has a value for the more difficult x=0 and y=0 case.]
Interestingly, using this definition, we would have
=
=
=
Hence, we would find that rather than
. Granted, this definition we’ve just used feels rather unnatural, but it does agree with the common sense notion of what
means for all positive real numbers x and y, and it does preserve continuity of the function as we approach x=0 and y=0 along a certain line.
So which of these two definitions (if either of them) is right? What is really? Well, for x>0 and y>0 we know what we mean by
. But when x=0 and y=0, the formula doesn’t have an obvious meaning. The value of
is going to depend on our preferred choice of definition for what we mean by that statement, and our intuition about what
means for positive values is not enough to conclude what it means for zero values.
But if this is the case, then how can mathematicians claim that ? Well, merely because it is useful to do so. Some very important formulas become less elegant to write down if we instead use
or if we say that
is undefined. For example, consider the binomial theorem, which says that:
=
where means the binomial coefficients.
Now, setting a=0 on both sides and assuming we get
= =
=
=
=
where, I’ve used that for k>0, and that
. Now, it so happens that the right hand side has the magical factor
. Hence, if we do not use
then the binomial theorem (as written) does not hold when a=0 because then
does not equal
.
If mathematicians were to use , or to say that
is undefined, then the binomial theorem would continue to hold (in some form), though not as written above. In that case though the theorem would be more complicated because it would have to handle the special case of the term corresponding to k=0. We gain elegance and simplicity by using
.
There are some further reasons why using is preferable, but they boil down to that choice being more useful than the alternative choices, leading to simpler theorems, or feeling more “natural” to mathematicians. The choice is not “right”, it is merely nice.







We’ve had some problems with “HTTP-Everywhere” messing up the LaTex (one of our readers figured that out). If you can turn off that plugin, it should clear up.
If that’s not the problem, let me know if you figure out what is!
See also: Indeterminate form.
Pingback: Q: What does 0^0 (zero raised to the zeroth power) equal? Why do mathematicians and high school teachers disagree? | Ask a Mathematician / Ask a Physicist « ennovates blog
If zero represents an absence of value, then like how values can’t be divided by zero, zero cannot be raised to the power of zero.
Essentially what you want to do is multiply nothing by nothing because nothing =0 and 0=0. But the equation should be null and voided from the start.
Without the fancy mathematics, let me demonstrate.
Stick both of your hands out, palms up. Nothing is in either heither hand. Clap them together, and we see 0+0 is 0. Pull them apart and you see 0-0=0. Now take the nothingness in one hand and multiply it by itself. Not possible because there isn’t anything there to do so with. Have mathematicians forgotten math is an intellectual concept and on itself, one big variable that we use to relate to tangible things.
So regardless of what the numbers equate to 0^0 isn’t 1 or 0. It’s impossible because nothing cannot be multiplied by itself. Tell this problem to a robot and his head would spin and springs and screws would fly out right before he said critical error and exploded. Lol
Pingback: Dosis de links 24/08 | IdentidadGeek
I’m sorry, real world app, but you are mistaken. That kind of reasoning was used to shut down the idea of Imaginary Numbers (hence their name), as well as toward the concept of zero (which you seem to be fine with in some contexts, but not others), and towards fractals. The more amazing our mathematics becomes, the more trouble you will have claiming that math is just there to relate to tangible things.
It’s 1.
#include
#include
int main(int argc, char **argv)
{
printf("%f\n", pow(0.f, 0.f));
}
% ./zerotozero
1.000000
Windows Calculator also thinks that 0^0 = 1
MS Mathematics says its indeterminate
Pingback: “…a miniscule amount of obliteration still obliterates you.” | SebastianMarshall.com: Strategy, Philosophy, Self-Discipline, Science. Victory.
In the study of tetration or iterated exponentiation infinite power towers are probably the oldest aspect of tetration researched. Some infinite power towers diverge, for example the infinite power towers of 2 diverge. Some infinite power towers converge like the infinite power towers of 1 converge to 1. And then some infinite power towers display periodic convergence. The infinite power towers of 0 happen to be in the center of a circular region of period 2 convergence. Thus it is natural to claim that 0 = 0, 0^0 = 1, 0^(0^0) = 0 and so forth.
I feel that the cleverest student’s solution is correct. The question is what is y(x) = x^x for y(0)? If we can’t start with y(0) we can determine lim x -> 0 y(x). Some of the above solutions are effectivly parametric equations trying to calculate y^x as lim y -> 0 and lim x -> 0. This is over complicating things. Basically, we can use a version of L’Hopitals rule. According to some of the above arguments, we shouldn’t be able to calculate x/x for x=0. L’Hopitals rule tells us that as lim x -> o x/x goes to 1.
No es por que las computadoras quieran que sea 0 ala 0 es 1 , en verad 0 ala 0 es indeterminado y eso el lo unico. Las computadras botan 1 por que hay una razon supongo de la estrucctura del codigo, pero no lo se exactamente.
Pero no es porque es 1.
We life in the real world. not this wonderland where multiplying nothing by nothing gets you something.
A math system should be judged by if it follows the laws of reality. If it does stuff that’s impossible (like creating something from nothing) then the system has no meaning and no boundaries for its definition. Math exists within our universe and so it is governed by the laws of our universe laws that are superior to the “laws” of math.
I think this whole discussion is based on the assumption that 0 actually exists.
Nonexistence can only be measured in its relation to existence. Everywhere within our universe we just see a whole bunch of “something” not “Nothing.” even “space” is a something in the sense that it exists and nothing is the lack of existence.
You can use nonexistance when your talking about things that exist like saying “how many ninjas do I have in my hands? None. I have no ninjas.” The only reason that idea of nothing can exist is because it relates to the idea of existance e.g. ninjas exist but they do not exist in my hands. something else exists in my hands. namely, candy (ooh. yum)
ECMAScript says 1 as well.
Math.pow( 0, 0 ); // 1
Mike, L’Hopital says that you can extend a function for an undefined spot by using his rule. Being able to extend it does not mean to find a (formerly somehow hidden) value for an undefined spot, it is just an extension, the creation of a new function. You can raise this new function to the “social level” of a definition for the original term, then. And in this process you may be able to choose one of many options. The problem of 0/0 is similar.
lim x→0 of 0/x is 0
lim x→0 of x/x is 1
lim x→0 of x/0 is (undisputably) undefined.
So for 0/0 mathematicians chose the last option. In case of 0⁰ they chose the option of defining it according to lim x→0 of x⁰. —Alfe
If x has more divisors than y, then x> y. Because 0 is any integer divisible “him” it is greater than any integer. Although it seems small here as it is “great” …
Pingback: It’s the small things…
If we hope
0^(-0)=1/0^0
(0^0)^2=0^(0*2)
(1-1)^0=C(0,0)*1^0*(-1)^0
to be correct,
defining 0^0=1 is the only choice.
To avoid
0=0^1=0^(2-1)=0^2/0^1=0/0
0 to negative power or 0 as denominator should be forbidden.
Therefore 0^0 is irrelevant to 0/0.
Continuity is not a necessary consideration.
0^0 can be defined as 1 even if it is not continuous.
Conclusively,
defining 0^0 as 1 is reasonable.
On the contrary,
defining it as other values or not defining it is ridiculous.
Please can you write the following tedious arithmetic in a proper way.
Example:
3.,220,000 and /9 and cube root = 7.0991189e+10
and /3 and cube root twice and squared = 202.000210
and squared again and /1.5 and square root twice x 1,000 = 1,284.260415
So I would like 3,220,000 being converted to 1,284.260415
Thanks
John D. Miller
Continuity is a necessary consideration.
0^0=1 is useful in some areas.
Conclusively, defining 0^0 as 1 is reasonable.
On the contrary,
not defining it or defining it as another value is ridiculous.
You cannot get something from nothing when you start out with 2 nothings. That is logical. To say that I can get something when I have nothing to start with is irrational. Of course the exception is the government who thinks when you have nothing you can get something…more debt. Still totally irrational…and very expensive.
17^0=1
125^0=1
0^0=1
Seems rational to me…
Nothing to the power of nothing isnt anything! STOP confusing the children with your imaginanry numbers! 0^0 = 0 to say other wise is just WRONG!
Article needs more sourcing as to what mathematicians belief. After all, the following University of Utah website, written by mathematicians, says that it is undefined: http://www.math.utah.edu/~pa/math/0to0.html
Does the author have a source showing that it is held widely as an accepted convention that 0^0 = 1?
There is a basic ambiguity : You cannot discuss about 0^0 without specify the related field of matematics (set theory, or elementary algebra, or topology, or…). i.e; :
http://www.scribd.com/JJacquelin/documents
“Zero to the Zero-th Power”, translated from “Zéro puissance zéro”
Category theorists view numbers as being embodied by sets. For example, the number zero can be viewed as being represented by the null set. The number one contains as its one member, zero (or the null set). Two contains zero and one as its two members, etc. This is standard (both the convention used and the notion of using sets to represent numbers).![A \times B = [(a,b)| a \in A and b \in B] A \times B = [(a,b)| a \in A and b \in B]](//s0.wp.com/latex.php?latex=A+%5Ctimes+B+%3D+%5B%28a%2Cb%29%7C+a+%5Cin+A+and+b+%5Cin+B%5D&bg=ffffff&fg=000&s=0)
![A + B = [(a,C1)] \cup [(C0,b)] A + B = [(a,C1)] \cup [(C0,b)]](//s0.wp.com/latex.php?latex=A+%2B+B+%3D+%5B%28a%2CC1%29%5D+%5Ccup+%5B%28C0%2Cb%29%5D&bg=ffffff&fg=000&s=0) for
for  not in
not in 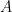 and
and  not in
not in 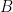
 , then, is the set of functions from
, then, is the set of functions from 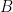 to
to 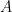 .
.
Products are then defined (for the category of finite ordinals, they are defined uniquely) in the usual manner:
Coproducts (sums) are also defined:
Exponentiation
Example:
2^3
2 = {0, 1}
3 = {0, 1, 2}
2^3 =
{
{0|->0, 1|->0, 2|->0},
{0|->0, 1|->,0 2|->1},
{0|->0, 1|->1, 2|->0},
{0|->0, 1|->1, 2|->1},
{0|->1, 1|->0, 2|->0},
{0|->1, 1|->0, 2|->1},
{0|->1, 1|->1, 2|->0},
{0|->1, 1|->1, 2|->1}
}, which is 8.
Therefore, 0^0 = 0 if we say that there is no function from the empty set to the empty set. However, most mathematicians will agree that there is (albeit vacuously), such a function. Therefore, 0^0 = 1.
a^3=1*a*a*a
a^2=1*a*a
a^1=1*a
a^0=1
There is no exception when a=0.
0^0=1 is reasonable.
K.R. O’Connell,
2^0=1
How do you explain something to power of nothing is something?
JJacquelin,
There is no ambiguity at all to 0^0=1.
A Nommy Moose,
How do you explain 2^0=1?
What is the sum of nothing?
You may answer 0 without hesitation.
But you may not Know how to explain it.
Because 0 is the identity element of addition.
Adding 0 is eqivalent to not adding anything.
Therefore the sum of nothing is 0.
Similarly, what is the product of nothing?
Since 1 is the identity element of multiplication,
the product of nothing is 1.
This concept explains not only 0^0=1,
but also 0!=1.
i really don’t get it but if anything to the power of zero equals 1 than this makes since:
17+84-(27+63-5)^0-(12/6)*5+3-4+8-7*4^0=0
Pingback: L’Hôpital’s Rule « Thoughtspresso
Ok so one of the big problems I notice in the comments is there are two fundamentally different ideas of what mathematics is.
On the one hand normal people think that mathematics ought to be the study of the concepts of measure and quantity etc from the real world. The test for what a definition ought to be is how well it fits the real world and our intuitions. So David says “A math system should be judged by if it follows the laws of reality.”
The other idea is the mathematicians. To a mathematician the basic ideas are up for grabs. If you want to define a thing that looks a lot like a normal concept but actually acts in a totally different way that’s fine. The point is to study interesting made up things, not to explain our intuitions or our world.
The problem is presenting ideas in terms that have a clear intutivie meaning, but in fact meaning something different. The classic example is summing divergent series. You will often find the claim 1+2+3+4…=-1/12. This is an easy to decode shorthand for a meaningful and sensible idea if you are a mathematician who knows about zeta function regularisation. If you are not it can only be interpreted at face value, ie that adding all the integers together gets to -1/12. This is false and obviously so. That is not the claim being made. The claim being made is that zeta(-1)=-1/12, that is a well defined and sensible thing to say.
When some mathematicians say 0^0=1, others 0^0=0 and others 0^0 is undefined it looks like they’re disagreeing. Because it looks like 0^0 is an intuitively understandable idea that ought to have exactly one answer. But what is actually meant is 3 separate notions, chosen not because of reality or meeting intuitions but simply because they produce interesting things to study.
One problem everyone has understanding mathematics is assuming that intuition about how numbers and shapes work ought to be a good argument. That’s not the game modern maths plays. Maths for call it 100 years has been a game played with symbols that look like but really really are not common ideas. The fact that insane things result isn’t because mathematicians are crazy (though they are that) or wrong. It’s because you think they mean what it looks like they’re saying. They’re not, they’re playing a game, the are 100% not talking about the world.
Some mathematicians say 0^0=1,
others say 0^0 is undefined.
Nobody says 0^0=0.
Continuity should not be the only point of view.
Take more points of view into consideration,
defining 0^0=1 is the only reasonable decision.
Nothing with nothing dimension… the natural qubit we are running on
So, should this be considered alright?:
0^0 = 1
0^0 = 10^(log(x^0)) = 10^(0*log(x))
= 10^0^log(x) = 1^log(x) = log(x) = 1 when x–>0+
or this?
0^0 = 1
log(0^0)= 0*log(0) = log(1)
10^0^log(0) = 1^log(0) = 1 = 1^1
=> log(0)=1
or perhaps
1^0 = 1
log(1^0) = log(1)
0*log(1) = log(1) = 1*log(1)
identifing terms: 0 = 1
By the way, I like best:
0^0 = 1
0^0 = 0^(1-1) = 0^1/0^1 = 0/0 = 1
x^y=e^(y*log(x))
is invalid for x=0.
log(1)=0
I agree that exp(y*ln(x)) is not valid for x=0, I beg your pardon. But I admit that, after stating
0^n = 0 if n>0,
0^0 = 1 (n=0) gets a bit confusing.
I can’t see a reason (besides possible ‘practical’ arguments) for
1=0^0=0^(1-1)=0^1/0^1=0/0
As said above: «To avoid
0=0^1=0^(2-1)=0^2/0^1=0/0
0 to negative power or 0 as denominator should be forbidden.
Therefore 0^0 is irrelevant to 0/0.»
Now, going back to:
if a) 0^0 = 1
and b) 0^1 = 0
turns out that dividing b) by zero, unexpectedly converts 0/0 into 1.
Summarizing:
Number zero seems to behave in a fanciful way: as nul element in addition, as zero in multiplication; is mostly infinity or indeteminate when dividing, is zero raised to any positive power but one if exponent is zero; negative powers are forbidden; logarithms are not valid… All together, sounds a bit disturbing.
Index laws are not totally valid for base 0.
There is no reason for
0^(1-1)=0^1/0^1
to be valid.
There are some restrictions to 0.
You don’t need to be confused.
Just accept it.
I don’t know. I would think 1 but 0 doesn’t have a value in the first place
Math does not talk about the world. Math is meaningless. WE give the symbols of math meaning when WE interpret them as, for example, the relationship between distance and time during the free fall of an object. There is nothing in the equations of motion THEMSELVES that correspond to ANYTHING in the world. Look at the math behind economics. A lot of it is either similar or identical with math from Quantum Mechanics or Statistical Mechanics. This would be pretty odd is math had some sort of intrinsic connection with the world.
That being said, there seems to be some confusion about what “value” means from a mathematical standpoint. “Value” has nothing to do with “amount” as David Umstattd explicitly argues for, and many others appear to believe. In math, the “value” of a number is nothing over and above its POSITION with respect to other numbers. Zero isn’t “nothing.” Zero is location implicitly defined by other numbers and a hos of operations. The intermingling of math and metaphysics has been a thorn in the intellectual side of humanity for quite some time now.
Math is a human construction. A tool (no different than a hammer) that we use to do certain things. The only standards math need be held to, are the ones we (rather, mathematicians) create. There is no more.
consider 1/1 =2/2 =3/3=……. =k
(1+2+3)/(1+2+3)=k , (1+0)/(1+0)=(1/1)=(0/0) ,similarly for 2/3 , ….. so 0/0 can take any value,
i.e one value at a time for that 0/0
e.g:
1*(0/0)=2*(0/0) ,here 1st o/o takes 2 ,2nd takes 1 as the value
so 0/0 is undeterminate so 0^0 which is 0/0 is undeterminate
but it can take 1 as the value for one case(particular)(only one at a time)
similarly 0 for another case…….
aj,
If you think 0^0=0^(1-1)=0^1/0^1=0/0
then 0=0^1=0^(2-1)=0^2/0^1=0/0
Therefore 0^0 is irrelevant to 0/0.
0^0=1
but 0/0 is indeterminate.
So funny. If I explain as following:
a) 0/0 = 0*(1/0) => division by zero —->For mathematics: undeterminate; For programmers: error.
b) And if we know, 0^0 = 0*0*…*0 (0 times) and of couse equal 0.
By vision, I don’t see 1 :))