Q: Why does the Earth orbit the Sun?

The original question was: What exactly causes the Earth’s rotation and revolution?  Does this occur due to centripetal force and the lack of friction to stop the Earth from spinning? IE- Newton’s First Law? If so, where did this centripetal force come from? Was it a product of this rock being hurled through space and stuck in the Sun’s pull? As for the rotation, I don’t even have a guess. Are there planets that don’t revolve at all, or is that a necessity?

Physicist: I’ll break this down into two questions: “Where does the rotation originally come from?” and “Once the a planet is in orbit, what keeps it there?”

Where does the rotation originally come from?: The original yearly rotation of the Earth around the Sun (orbital rotation), as well the daily rotation of the Earth about it’s own axis (just “rotation”) is essentially dumb luck.

If you hold out any object and toss it in the air, you’ll find that it’s almost impossible to toss it in such a way that it doesn’t turn at all.  The same is true of stellar nebulae (the gigantic clouds of gas and dust that condense to form stars and planets).  They always have at least a little bit of swirl and spin.

As the cloud that became our solar system collapsed inward, the mass settled into a spinning disc with a big bump in the middle (the Sun), and that disk began collapsing even more to form the planets.  This process is called accretion, and you can see it at work over and over again.

When stuff collapses it tends to form a central ball and a disk.

There aren’t any non-spinning planets, but the speed that they spin varies widely.  Jupiter’s day is only 10 hours long, while Venus’ is around 240 Earth days long.  How fast and in exactly what direction a planet will end up spinning is a fiendishly complicated problem.  Some of it is determined by the flow of the gas and dust of the “proto-planetary disk” (which is fairly simple), which is why the orbits and rotations of every planet in the solar system orbits and rotates in roughly the same direction.

Since the Earth orbits the sun in the same direction that it rotates, when it's morning (6 am) you're standing on the "front side" of the Earth.

But once the ball gets rolling (so to speak) you find yourself with a solar system full of big rocks on slightly different orbits slamming into each other, and changing each others rotations.  For example, the Earth’s moon was (most likely) created by a stupendous collision with something Mars-sized that “splashed” the moon into orbit.  That impact, as well as tidal effects from the moon itself, have radically changed the length of the day on Earth.  Uranus is also believed to be the victim of an even bigger collision that tilted it’s rotation axis around 98° from it’s orbital axis (the direction perpendicular to its orbit), and dramatically changed the length of it’s day.  We can’t say by how much; no one saw what it was like before.

So, in general, things spin because they collapse from very large clouds of stuff that were spinning (just a little) already.  If the cloud hadn’t been spinning, then all of the mass in the solar system would have fallen all the way into the Sun.  Instead, a mere 99.86% of the solar system’s mass is in the Sun.

Once a planet is in orbit, what keeps it there?: Gravity pulls the Earth in, and centrifugal force holds it out.*  The centrifugal force on the Earth is just a result of the Earth moving in a curved path around the Sun.  It doesn’t slow down because there isn’t any friction.  After all, in space, there’s nothing to have friction with.  Why exactly an orbit is stable involves a short romp in math town.

Gravitational force, F_g, is given by , where G is the gravitational constant (dictates how strong gravity is), M is the star’s mass, m is the planet’s mass, and R is the distance between the planet and star.  It’s negative because it’s trying to decrease R.  You can use this to find the gravitational potential, U_g, by taking the anti-derivative: .  Force is the negative of the derivative of potential, which is fancy-speak for “stuff wants to fall downhill”.

Centrifugal force, F_c, is given by , where m and R are the same and v is the “tangential velocity” (how fast the planet is moving around the star, and not counting motion toward or away from the star).  There’s a handy way to rewrite this in terms of angular momentum.  Angular momentum, L, is always constant and (in this case) is given by .  Re-writing F_c in terms of L gives: .  You can use this to find the “centrifugal effective potential”, U_c.  “Effective” is just a physicist’s way of saying “I know, I know; the centrifugal force isn’t a ‘real’ force.  Just be cool for, like, two minutes.”. 

Looking at the total potential, U=U_g+U_c, it becomes clear why orbits can be stable.  In order to picture forces better physicists will sometimes draw “potential diagrams”.  A potential diagram is just an intuitive way of describing energy and, in turn, forces.  To understand it, imagine putting a marble on the line and think about how it will roll.  In the picture below the marble will roll to the left, but no too far.

The total potential curve in terms of distance to the Sun. When a planet gets too close to the Sun the centrifugal force "rolls it away", and when it gets too far away the gravitational force "rolls it back". A stable or "bound" orbit is one without enough energy to roll out of the pit. This diagram helps explain why it's so hard to fall into orbit around something: If you start from far away, you have enough energy to get back there.

An orbit is stable when the energy of a planet is “cupped” by the total potential.  If it gets too far out the gravity pulls it back, and if it gets too close the centrifugal force pushes it back out.

Also, as if you needed another reason to be excited about living in this universe, orbits are only stable in two and three dimensions.  The force of gravity drops in the same way that the intensity of light or sound drops off (in our case: 1/R²), so if the dimension of your space is D, then the force of gravity is .  This yields a gravitational potential of  when D≥3, and when D=2.

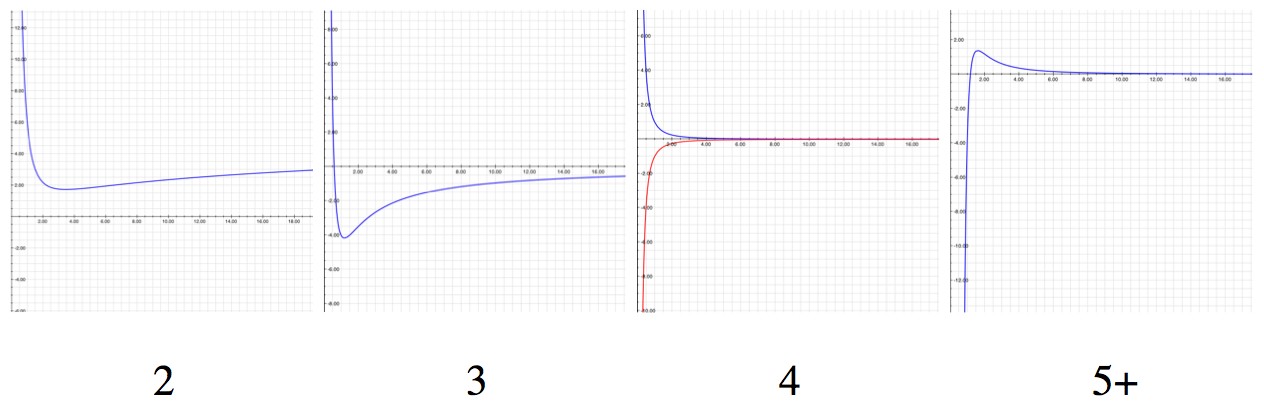
Gravity gets weaker, faster, the higher the dimension. In 1 dimension there's no circular movement and no orbits. In 2 and 3 dimensions the forces balance such that there are stable orbits. In 4 dimensions an object will either fall directly in or fly away forever (depending on its angular momentum). And in 5 or more dimensions gravity wins if an object is too close and centrifugal force wins if it's too far.

For small dimensions (2 and 3) the centrifugal force is stronger for small R and gravity is stronger for large R, which yields stable orbits.  For large dimensions (5 and up) gravity is stronger for small R and centrifugal force is stronger for large R, so the orbit is always trying to fly apart, one way or another.  In 4 dimensions the forces get stronger and weaker at the same rate (~1/R³), so if one is stronger than the other it’s always stronger.

*This isn’t technically true.  Technically the planet is moving in a straight line through curved spacetime, and experiences no centrifugal acceleration.  But whatevs.