Physicist: This is a follow up of this post, that would’ve been too long and meandering with this included. To sum up that post, a “measurement” is an interaction that exchanges information.
In the Copenhagen interpretation, what that measurement does is a magical rearrangement of the whole universe, faster than light.
More accurately (and here’s the answer), a measurement establishes an “entanglement” between the things involved.
A quick word about entanglement: Say you’ve got two marbles in a hat that are identical in every way, other than their color: red and blue. You and a friend each take out a marble without looking at it. You could have either one, but you don’t know which. What you do know, is that if you have the red marble your friend will have the blue marble, and if you have the blue, they’ll have the red. The marbles are correlated. If you each look, you’ll find that you never have the same color.
Obviously, your marble is in one state: either it’s red or it’s blue. In quantum mechanics however, a thing can be in multiple states, and amazingly enough, you can still have the same kind of correlation. You have a marble that is both red and blue (a red/blue “super-position”), and so does your friend, and yet they are both correlated such that they always have opposite colors. That is, just like in the non-quantum example, if you each look at your marble you’ll find you never have the same color. This multiple-state-yet-still-correlated thing is called “entanglement”. If you’re confused, then you’re awake. Back to the question:
Imagine that, for some reason, you and a friend get some pitching machines and start chucking baseballs at each other. Just to see if you can, you set up the machines so that they fire at the same time and the baseballs hit each other in mid-air. Now, pitching machines aren’t perfect, so the balls won’t always take the same path, just one that’s more or less forward. In particular, there’s no way to predict what angle they’ll hit each other at, and in what directions they’ll bounce apart.
After the collision there’s not a lot you can say about the trajectory of each ball. One thing you can say for sure is that, regardless of the direction one ball flies, the other ball will fly off in the opposite direction. After the collision their trajectories are correlated (maybe not perfectly, but follow me here).
Baseballs are pitched such that they bounce off of each other in mid air.
Now look at the same situation from a more “quantumy” perspective. The pitching machines throw the baseballs, not in one of many slightly different trajectories, but in all of the possible slightly different trajectories.
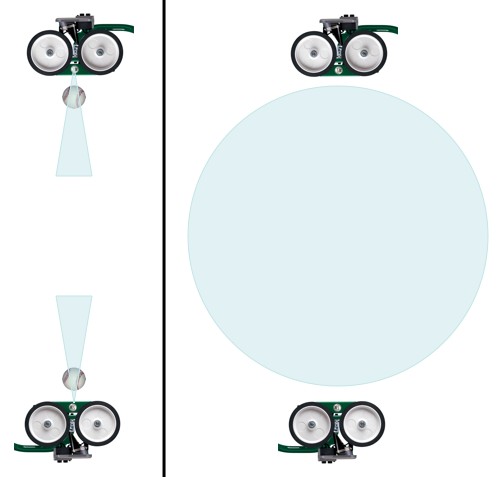
Each baseball, rather than following a single path, takes a super-position of every possible path (in a cone). After the collision the balls are still in a super-position of every possible resulting path, but must be traveling in opposite directions. Correlated super-positions = entanglement.
Clearly the collision conveys information, so it is a measurement. The information is pretty straight forward (“you are being hit by a baseball”), but it’s still informative. Surprisingly, the effect of that measurement depends on your perspective.
From an outside perspective: both baseballs move toward each other in many, uncorrelated, paths. A “baseball probability cloud”. I say that they’re uncorrelated because even if you know which path one of the baseballs is taking, you still know nothing about the other.
When they collide and bounce apart, they’re still traveling along a super-position of many possible paths, but now they’re correlated.
Their collision (and mutual measurement) has entangled their states.
From an inside perspective: each state of each baseball thinks of itself as the only state. An “inside perspective” means picking one state out of the many, and thinking about what it’s life is like (to be needlessly over-the-top exact; “…picking one bundle of indistinguishable states out of the many…”).
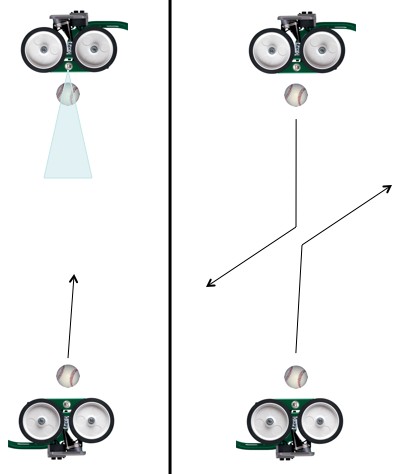
After it’s fired, if you look at just one state of the bottom baseball it looks “non-quantum” and follows one path. From its perspective the other ball is in a super-position of states. But, when they collide they measure each other, and suddenly see themselves and the other ball in just one state. Note that each of the different states experience this.
Before they collide, one ball sees the other ball as being in many states. When they collide they suddenly see the other ball as being in one state. So, from an “inside” point of view, measurement looks like “wave function collapse“, one of the great weirdnesses of the Copenhagen interpretation (“collapse” = “all but one state disappears”). When a ball bounces away from the collision it still sees itself going in one direction, and (since the balls always bounce in opposite directions) it’ll definitely see the other ball going in only one direction.
Their collision (and mutual measurement) has collapsed the state of the opposite ball (from the perspective of both balls).
But keep in mind that every state of both balls sees a (different) wave function collapse. There’s nothing special about either ball; they’re both in many states.
Just for fun, a very outside perspective: Say you’re in another star system, and you can’t get any real information about what’s going on. You see not just the baseballs in many states, but the people involved as well. After a collision, the people running the machines see the baseballs as being entangled. Now say one of them (Bob) tries to find one of the balls. When he does, he suddenly knows where the other ball is. Bob’s excited because he just experienced wave function collapse for the octillionth time that day. Also, since the balls were entangled, he’s instantly “collapsed the wave function” of the other ball (he now knows where it is).
But, from your very outside perspective, Bob’s many states are searching for the ball’s many states. Each of his many states eventually finds one of the ball’s many states. Now, from far enough out, we can’t tell where each of Bob’s states finds the ball. All we can say is that the wherever the ball is, that’s where Bob will find it. That is; the state of the ball that bounced east from the collision will be correlated with the state of Bob that finds the ball to the east of the collision. Both Bob and the ball are still in many states, but now they’re correlated. By finding the ball, Bob (in his many states) is now entangled with it.
Even more awesome, since the baseballs were already entangled with each other, by entangling with one, Bob entangles himself with both. That’s not too impressive from Bob’s perspective, but it can seem spooky from a very removed perspective.
Relevant video.
Pingback: Ninth Linkfest
Just a query i have with quantum measurements.
Can any being make this measurement? i.e. can a dog make a measurement that will render the quantum state null, or does this measurement process have to be from a conscious being like us?
Is it possible to test this measurement to see if the dog made no impact on the entanglement?
Not just any being, but any thing!
Consciousness doesn’t enter into it.
Unfortunately, checking someone (something) else’s measurement is the same as actually making the measurement yourself.
ok, I must be misreading, so you can use the properties of entanglement so long as you do not observe / measure?
I did a post a while back about what happens when you interact with entangled particles.
Basically; yes. If you measure either entangled particle, you’ll break the entanglement (the particles will “decohere”).
I wonder if the results of the double slit experiment ( http://www.youtube.com/watch?v=DfPeprQ7oGc ) are really just artifacts of the size of measurement tool?
Let me explain:
If the photon goes through both double slits as a wave when it is unobserved, but it goes through only one slit as a particle when observed, couldn’t that simply mean that the way we measure (or observe) the photon is causing the change?
Don’t say “Yes” too quickly.
In our world of watching horses race around a track, the photons hit the horses and do not modify the horses’ behavior because the size of photon is insignificant from a horses’ perspective. But if we could watch the photon go through the double slit experiment with something that is billions of times smaller than a photon (let’s call it a “Speck”), then the photon would not be disrupted and would retain it’s wave properties.
Therefore, it’s not that the actual act of observing the photon in the double slit experiment that is the issue, the real issue is the relative size of what we use to measure where the photon is — that’s the real issue. The theoretical Speck would be smaller and not disruptive like the way we measure photon’s today.
By the way, how do we watch the photon go through the double slit as a particle today? We shoot something at it to “see” it?
So if the above is true, then we don’t have the paradox that the photon is in multiple places at the same time.
Thanks,
Rick Ragan.
Some of the tricks for determining which slit the photon went through are covered near the bottom of this post.
Pingback: Skammtafræðileg athugun | Manntal
Pingback: Q: If quantum mechanics says everything is random, then how can it also be the most accurate theory ever? | Ask a Mathematician / Ask a Physicist
Pingback: Q: What is quantum teleportation? Why can’t we use it to communicate faster than light? | Ask a Mathematician / Ask a Physicist
That last part blew my mind up. I’ll never see the world as I used to see.
Thx for all these posts Mr. Physicist
MWI to the rescue as always. no complaints though. perhaps to some this may be a better way to look at it:
to begin with, everything that can / has / will happen, did – assume that the universe is filled to the brim with all possible histories and futures within the limits of what physics permits to happen. in other words, take the universe as literally the universal set of everything in all aspects, dimensions, the lot.
this doesn’t say much on its own. however. the moment you start imposing restrictions (lets say, energy conservation) a curious thing will happen – events that are now prohibited (eg, events violating energy conservation) can no longer exist. remember that this initial universe (kind of) is a complete and total collection of everything, even (at first) things / events / situations / states that would not be possible or could not exist today.
what this teaches is that reality is total collection of all possibilities that are allowed to happen – reality is best defined by its tendency to ‘erase’ or ‘hide’ contradicting or impossible events, rather than focusing on events we expect to happen which are strictly tied to singular experiences (in the sense that you can’t experience alternate realities at the same time, only one path through them). this also serves to better demonstrate the nature of interactions at the quantum scale.
to that i have to say the collision example is likely the best at explaining this principle… you have a universal rule (conservation of momentum), and because this rule establishes relationships (when 2 things collide), your reality has been narrowed down to as many states as there could exist where this rule / relationship is unbroken for as long as the rule is valid (all universes, possibilities where conservation of momentum holds).
one other thing to note – this approach allows for variable laws of physics. it is my belief that without some operating restrictions or rules (laws of physics), you would have literally everything possible happening and a question of stability isn’t even relevant (stability is itself a rule / measure). therefore i don’t think physics-violating universes could exist, since it makes no meaning for our universe (or anything in it) to interact with one where the same laws of physics don’t exist – a very blunt example, a universe without time has no meaning interacting with a universe that has time (or any physical law for that matter).
if you’re wondering what would happen if this cross-universal-laws interaction would result in… my guess is a one-way flow (net) of entropy. eg, in a hypothetical universe B where some conservation law is allowed to be violated, only the events / resultants of events where this conservation law happens to have held would be permitted to exist in / interact with universe A. this means that potentially anything in universe A can enter universe B, but only (for example) half the particles/energy in B could enter A. conversely, B receives a relatively ordered / consistent flow of energy / particles from A, but A receives a relatively random assortment. in this picture the flow from B to A increases entropy of the transitioning energy / particles while entropy is reduced the other way around.
that aside, for practicality it makes sense to pick some already-restricted universe, such as one where people exist to invent baseballs and ponder their motion.
i guess very broadly i can say that measurement is the act of imposing a correlation, or more liberally speaking, measurement and the flow of entropy are related and perhaps one and the same phenomena.
My question to the Physicist is when any object in superpostion is observed it collapses to one particular state, what determines the nature of that state for example, when light passing through a double slit experiment when observed becomes particles, what determines the reduction of light to particles from several possibilities and why has it to be reduced to particles whenever observed?