Q: How do those “executive ball clicker” things work?

Posted on August 10, 2011 by The Physicist

The original question was: With the game for executives, consisting of several metal balls hanging in a straight, horizontal row (a “Newton’s cradle”), when one ball is lifted and let loose to hit the rest of the row, only one ball at the other end gets swung away in its arc. And so the is case with two balls with two balls, and with three balls the response is with three balls, etc.

The question: Why the reaction to one ball is always one ball and not two balls to a shorter distance, or the reaction to three balls, one, or two balls to a greater distance, etc?

Physicist: For those readers who haven’t seen one of these since the 80’s, here’s what we’re talking about.

How do CEO's get any work done?

In every collision you have conservation of momentum. But, when things collide they can heat up, produce sound, or otherwise lose a little kinetic energy. For example, when you throw two blobs of clay straight at each other: they start out moving, but after the collision they stick together and barely move. The collisions that lose energy like that are called “inelastic collisions”.

When a collision conserves energy it’s called an “elastic collision”. As you might imagine, steel balls don’t change shape much when they collide: the collisions are elastic and do conserve kinetic energy almost perfectly.

For a momentum-and-energy-conserving-collision between two balls, one of which is stationary, you can show that the only way for everything to balance out is for the balls to “switch”.

To extend this to the full multi-ball executive ball clicker, you can think of the whole thing as just a string of two-ball collisions. Ball one hits ball two hits ball three … and each time all of the movement is transferred from one ball to the next. The exact same idea is responsible even when you swing several balls at the same time: it’s just a string of very rapid two-ball collisions.

If you were to build one of those executive ball clickers with rubber or wooden balls (which would absorb a little kinetic energy) you’d find that you’d get all of the balls moving, instead of just the one on the far end. The one-ball-in/one-ball-out thing only works with very solid balls.

Answer gravy: The nice thing about a Newton’s Cradle is that the impacts happen in only one direction, which makes the math much easier.

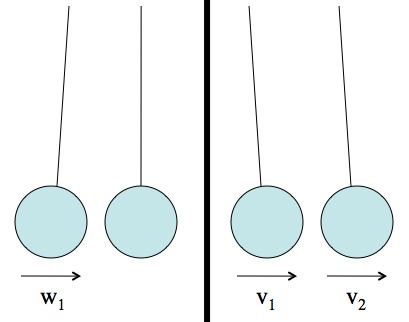
The before (left) and after (right) velocities. Showing that executive ball clickers work boils down to showing that v1 = 0.

If the mass of every ball is $m$ , the velocity of the original moving ball before the collision is $w_1$ and the velocities of the two balls after the collision are $v_1, v_2$ , then:

Conservation of momentum can be written: $mw_1 = mv_1+mv_2$

Conservation of energy can be written: $\frac{1}{2}m w_1^2= \frac{1}{2}m v_1^2+\frac{1}{2}m v_2^2$

You can clean these up a bit to get $w_1 = v_1+v_2$ and $w_1^2=v_1^2+v_2^2$

$\begin{array}{ll}\left\{\begin{array}{ll}w_1 = v_1+v_2\\w_1^2=v_1^2+v_2^2\end{array}\right. \\\Rightarrow\left\{\begin{array}{ll}w_1^2 = (v_1+v_2)^2\\w_1^2=v_1^2+v_2^2\end{array}\right. \\\Rightarrow (v_1+v_2)^2=v_1^2+v_2^2\\\Rightarrow v_1^2+2v_1v_2+v_2^2=v_1^2+v_2^2\\\Rightarrow 2v_1v_2=0\\\Rightarrow v_1=0 \textrm{ or }v_2=0\\\end{array}$

Using that result, and remembering that w₁ = v₁+v₂, the only two possible solutions are “v₁=w₁, v₂=0″ or “v₁=0, v₂=w₁“. The first solution would imply that the first ball ignores the second and moves through it. The second solution is what you see: the impact switches which ball is moving and which is stationary.

In the case of an inelastic collision you have a larger initial kinetic energy and a smaller final kinetic energy. Energy conservation can then be written: $E_{initial} = E_{final}+\ell$ or $\frac{1}{2}m w_1^2=\frac{1}{2}m v_1^2+\frac{1}{2}m v_2^2+\ell$ , where $\ell$ is the energy lost to heat or sound. Running through the same math as above you’ll find that $v_1v_2 = \frac{\ell}{m}$ . Suddenly that last “one of them has to be zero” step doesn’t work, and you find that the kinetic energy has to be divided up between the balls.

This question was surprisingly tricky. The fact that the balls are arranged in a line turns out to be very important. If the impacts aren’t in a straight line, or if the first ball hits more than one other ball at a time, then the “executive ball clicker effect” goes away.

This entry was posted in -- By the Physicist, Math, Physics. Bookmark the permalink.

18 Responses to Q: How do those “executive ball clicker” things work?

Christopher Hockenbrocht says:

August 11, 2011 at 9:56 pm

Sorry, but I’m pretty sure you have elastic and inelastic mixed up. Those balls are pretty elastic while clay is pretty (quite) inelastic as it does not conserve it’s shape.

Otherwise, very nice.
Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:

August 11, 2011 at 10:20 pm

Thanks! You are utterly correct.
Fixed.
I swear, if it weren’t for my “L” and “R” tattoos I wouldn’t know right from left.
Megan says:

August 13, 2011 at 4:25 am

I’m sorry if this sounds silly, but I don’t really understand the way the conservation of energy formula is written out?
Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:

August 13, 2011 at 10:20 am

Not at all! It’s on me if I didn’t explain things well.
Kinetic energy (the energy tied up in movement) is given by: $E = \frac{1}{2}MV^2$
If you look at the second picture in the post, the total kinetic energy before the collision is $\frac{1}{2}mw_1^2 + \frac{1}{2}m0^2 = \frac{1}{2}mw_1^2$ , since the first ball has mass m and speed w₁ and the second ball has speed 0.
After the collision the first ball has speed v₁ and the second has speed v₂. They still both have mass m, so after the collision the kinetic energy is $\frac{1}{2}mv_1^2+\frac{1}{2}mv_2^2$ .
Since we’re saying that energy has to stay the same, the before and after kinetic energies have to stay the same: $\frac{1}{2}mw_1^2 = \frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2$ .
mike says:

August 27, 2011 at 11:17 pm

well on this though i like your answer i will have to ask another question i forget who said it ( for every action there is an equil but opposite reaction) your answer indicates that he was wrong in this case when the balls hit one another you are saying they are dispurseing energy insted of transfering it thus loosing some momentum witch i agree with do you agree
Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:

August 27, 2011 at 11:52 pm

Newton said it, and that dude was right!
“The equal but opposite reaction” is another way of talking about conservation of momentum.
The balls can lose energy fine, but momentum is always conserved.
Imaginascience says:

September 14, 2011 at 1:53 pm

Actually, named recently (1967) “Newton cradle” after Newton, perhaps because the latter made experiences with pendulums (but to assess weight vs mass) . Yet, Newton was far more interested to see what happens when the length of each pendulum is different (or matter used for the pendulum).
Ty Brannon says:

March 2, 2012 at 1:29 pm

For how long can a Newton’s Cradle sustain momentum? Do you know if there’s a record? Thanks
Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:

March 2, 2012 at 4:43 pm

No idea.
I don’t think there’s any theoretical limit. 10 bucks says there’s some kind of massive international competition!
Raj says:

July 20, 2012 at 12:41 am

Here is a very good video of various experiments with the Newtons’ cradle.
katie wright says:

May 7, 2013 at 8:43 am

I have a question. In the second picture on the post it says “showing the executive ball clickers work comes down to proving v1 equals zero” and then you have the math listed below. I understand how you got v1 ans v2 to equal zero but my question is, how does v1 equaling zero prove newtons cradle works?
Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:

May 7, 2013 at 11:12 am

What’s spooky about a Newton’s Cradle (I think) is that the initially swinging ball comes to a complete stop, which is “v₁=0″. I suppose there are other ways of defining whether or not a Newton’s Cradle is “working”.
katie wright says:

May 8, 2013 at 8:18 am

I have to explain newtons cradle for a high school project and since you appear very knowledgeable of the subject, I was wondering if you could clear some things up for me. When you pull one ball up and let it swing down and hit the other balls, its energy and momentum are conserved through the other balls until the last one, which swings out with the same velocity as the first one hit. But energy is lost through friction, heat, and sound so eventually the balls lose their energy and come to a stop. Correct?
Error: Unable to create directory uploads/2024/11. Is its parent directory writable by the server? The Physicist says:

May 8, 2013 at 9:20 am

@katie wright
Yup!
katie wright says:

May 9, 2013 at 8:34 am

Okay good. My teacher would like to see me use some formulas with numbers (opposed to just variables), is there any that come to mind where I would be able to calculate the numbers (like mass) and use them in the equation?
C D Wright says:

June 5, 2013 at 9:38 am

These things work best if, when at rest, the balls do not touch each other, but have a tiny gap. If they are in contact then there are multiple solutions that preserve both energy and momentum. With the gap(s) you can analyse it as a sequence of perfectly elastic two ball collisions.
Torina says:

November 21, 2013 at 10:31 pm

Thanks a lot. You helped me a lot.
Nurul Farahin says:

December 10, 2015 at 10:38 am

If this experiment is conducted using the ball made from wood, would there be any different in the results? Can you explain it to me?