Physicist: Light travels at different speeds in different materials. When you shine a beam of light from one material into another (like from air to water) it bends in such a way that the path it takes from one point to another requires the least possible time.
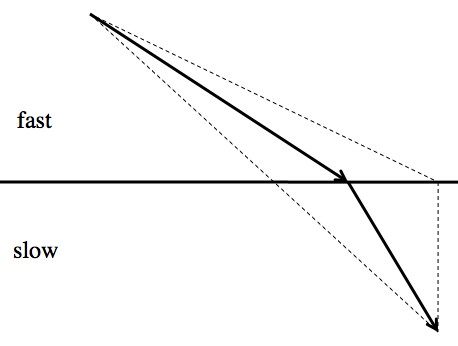
Taking a straight line means traveling through a lot of the “slow material”. Traveling through lots of “fast material” to make the path through the slow material as short as possible means taking a longer path overall (and taking more time). The path of “least time” is in between.
This should come across as deeply spooky. A particle that somehow “scouts the future” and then picks the fastest path to get where it’s going seems impossible.
And to be fair: it is. The crux of the problem is (as with damn near everything) wave/particle-ness. Particles can’t magically know what the shortest path will be, but waves find it “accidentally” every time.
First, check out the path that the “principle of least time” carves out. What follows is math, which some people dig. If you skip over the block of calculations, you won’t really miss anything.
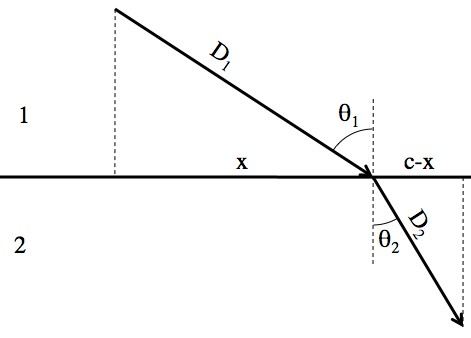
The time, T, that it takes to traverse a path is D/V, where D is the length of the path and V is the speed.
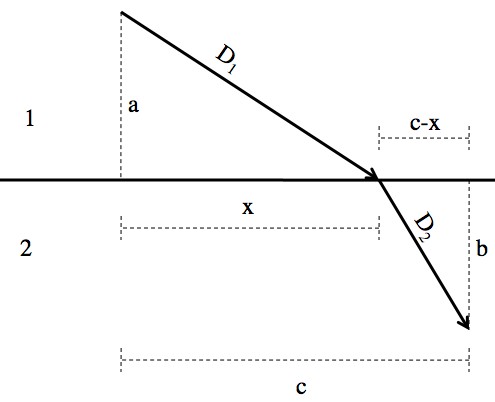
The picture for the derivation below. In the top material the wave speed is “V1” and in the bottom “V2”. With a little calculus, by sliding x back and forth you can find the “minimum-time path”.
By changing x you change the path, and the amount of time T it takes to move along that path. Calculus wonks may know that to find an “extremum” (either a maximum or a minimum), all you have to do is find the derivative, set it to zero, and solve. With any luck, those same wonks will be forgiving if I just declare that the following derivation finds the minimum time (and not a maximum or something) instead of proving that it’s a minimum.
![\begin{array}{ll}0=\frac{dT}{dx}\\\Leftrightarrow 0=\frac{d}{dx}\left[\frac{1}{V_1}\sqrt{a^2+x^2}+\frac{1}{V_2}\sqrt{b^2+(c-x)^2}\right]\\\Rightarrow 0=\frac{1}{V_1}\frac{1}{2\sqrt{a^2+x^2}}(2x)+\frac{1}{V_2}\frac{1}{2\sqrt{b^2+(c-x)^2}}(-2(c-x))\\\Leftrightarrow 0=\frac{1}{V_1}\frac{x}{\sqrt{a^2+x^2}}-\frac{1}{V_2}\frac{c-x}{\sqrt{b^2+(c-x)^2}}\\\Leftrightarrow \frac{1}{V_2}\frac{c-x}{\sqrt{b^2+(c-x)^2}}=\frac{1}{V_1}\frac{x}{\sqrt{a^2+x^2}}\\\Leftrightarrow \frac{1}{V_2}\frac{c-x}{D_2}=\frac{1}{V_1}\frac{x}{D_1}\\\Leftrightarrow \frac{1}{V_2}\sin{(\theta_2)}=\frac{1}{V_1}\sin{(\theta_1)}\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D0%3D%5Cfrac%7BdT%7D%7Bdx%7D%5C%5C%5CLeftrightarrow+0%3D%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5B%5Cfrac%7B1%7D%7BV_1%7D%5Csqrt%7Ba%5E2%2Bx%5E2%7D%2B%5Cfrac%7B1%7D%7BV_2%7D%5Csqrt%7Bb%5E2%2B%28c-x%29%5E2%7D%5Cright%5D%5C%5C%5CRightarrow+0%3D%5Cfrac%7B1%7D%7BV_1%7D%5Cfrac%7B1%7D%7B2%5Csqrt%7Ba%5E2%2Bx%5E2%7D%7D%282x%29%2B%5Cfrac%7B1%7D%7BV_2%7D%5Cfrac%7B1%7D%7B2%5Csqrt%7Bb%5E2%2B%28c-x%29%5E2%7D%7D%28-2%28c-x%29%29%5C%5C%5CLeftrightarrow+0%3D%5Cfrac%7B1%7D%7BV_1%7D%5Cfrac%7Bx%7D%7B%5Csqrt%7Ba%5E2%2Bx%5E2%7D%7D-%5Cfrac%7B1%7D%7BV_2%7D%5Cfrac%7Bc-x%7D%7B%5Csqrt%7Bb%5E2%2B%28c-x%29%5E2%7D%7D%5C%5C%5CLeftrightarrow+%5Cfrac%7B1%7D%7BV_2%7D%5Cfrac%7Bc-x%7D%7B%5Csqrt%7Bb%5E2%2B%28c-x%29%5E2%7D%7D%3D%5Cfrac%7B1%7D%7BV_1%7D%5Cfrac%7Bx%7D%7B%5Csqrt%7Ba%5E2%2Bx%5E2%7D%7D%5C%5C%5CLeftrightarrow+%5Cfrac%7B1%7D%7BV_2%7D%5Cfrac%7Bc-x%7D%7BD_2%7D%3D%5Cfrac%7B1%7D%7BV_1%7D%5Cfrac%7Bx%7D%7BD_1%7D%5C%5C%5CLeftrightarrow+%5Cfrac%7B1%7D%7BV_2%7D%5Csin%7B%28%5Ctheta_2%29%7D%3D%5Cfrac%7B1%7D%7BV_1%7D%5Csin%7B%28%5Ctheta_1%29%7D%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}0=\frac{dT}{dx}\\\Leftrightarrow 0=\frac{d}{dx}\left[\frac{1}{V_1}\sqrt{a^2+x^2}+\frac{1}{V_2}\sqrt{b^2+(c-x)^2}\right]\\\Rightarrow 0=\frac{1}{V_1}\frac{1}{2\sqrt{a^2+x^2}}(2x)+\frac{1}{V_2}\frac{1}{2\sqrt{b^2+(c-x)^2}}(-2(c-x))\\\Leftrightarrow 0=\frac{1}{V_1}\frac{x}{\sqrt{a^2+x^2}}-\frac{1}{V_2}\frac{c-x}{\sqrt{b^2+(c-x)^2}}\\\Leftrightarrow \frac{1}{V_2}\frac{c-x}{\sqrt{b^2+(c-x)^2}}=\frac{1}{V_1}\frac{x}{\sqrt{a^2+x^2}}\\\Leftrightarrow \frac{1}{V_2}\frac{c-x}{D_2}=\frac{1}{V_1}\frac{x}{D_1}\\\Leftrightarrow \frac{1}{V_2}\sin{(\theta_2)}=\frac{1}{V_1}\sin{(\theta_1)}\end{array}")
The angles for the last step above. This is also “Snell’s law”.
The exact value of x isn’t particularly useful. What is useful are those angles. The statement “
Snell’s law should look familiar to anyone who’s used to talking about waves going from one material to another. It describes, for example, the bending of light as it crosses between air and water.
So, the law of “least propagation time” is nothing more than a different, and far more difficult, way of stating “Snell’s law”. And again, if you’re talking about a particle, it’s hard not to think that the particle is testing each path in advance, and then taking the quickest one.
However, you can derive the same result by thinking about how waves propagate. Waves (light, sound, water, whatever) propagate perpendicular to their wave crests. Take a second: picture an ocean wave.
As one side of the crest enters a different material it changes speed. When different parts of the wave are traveling at different speeds the wave front as a whole changes direction.
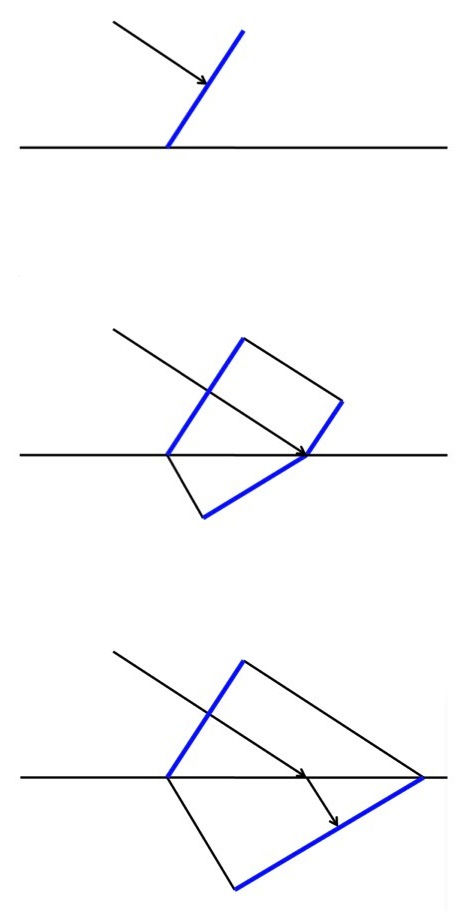
Top: a section of the wave starts to hit the boundary between two materials. Middle and Bottom: In the second material the wave moves slower. Since one side of the wave is moving faster than the other the wave front “swings around” into a new direction.
A good (but not quite accurate) way to picture the situation is to think of a car where the wheels on one side spin faster than the wheels on the other. Naturally, the car’ll turn to the side.
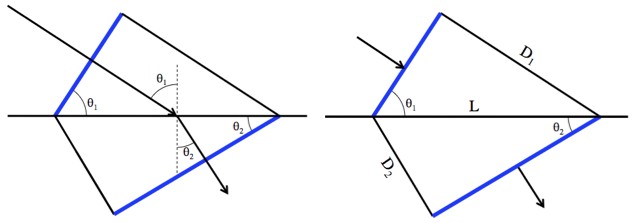
Left: the important angles, and where they show up in the triangles. Right: the angles and lengths involved in the math below.
You can be a bit more exact about this. The diagrams above describe a piece of the wave crest from the moment when one side hits the boundary, to the time the other side hits. Call that time “T” (why not?).
The distance that the top end of the piece-of-crest travels is D1 = V1T, and the distance the bottom tip travels is D2 = V2T. Now, using the definition of sine: 
Combining these you get:
Holy crap! Snell’s law again! Having the same result means that, in terms of behavior, the two approaches are indistinguishable. So, instead of a spooky particle scouting every path looking for the quickest one, you have a wave that’s just doing it’s thing.
The principle of least time is a cool idea, and actually makes the math behind a lot of more complicated situations easier, but at it’s root is waviness.
Pingback: Q: If light slows down in different materials, then how can it be a universal speed? | Ask a Mathematician / Ask a Physicist
I have heard something like this explained as a principle of least action, where “action” refers to a highly abstract physical notion.
http://en.wikipedia.org/wiki/Principle_of_least_action
That’s the “more complicated situation” I was thinking of.
I made a flash animation showing path selection via Fenman’s arrows method.
Pingback: Eleventh Linkfest
Thank you so much posting this. I knew about the principle of least time and I knew about Snell’s law, but I never made the connection before.
How does this prove that one of the theories is more correct than the other?
Just because we don’t know how a particle would be able to take every path simultaneously, we also don’t know why the wave crest would actually turn. Because this isn’t a water wave, and the wave crest itself isn’t physical – it’s the imagined barrier of all of the photons on the front of the light beam. We know of no reason why these photons would link together.
The math works for both, but the only on with any actual experimental evidence that supports it is the path of least action – the evidence being the double slit experiment.
The path of least time sounds pretty unbelievable, but so do many things we now know to be true in modern physics.
I have always disliked the “path of least time” argument, because it doesn’t easily relate to any physical principal.
As you showed here, Snell’s Law is easily derived from the wave model of light. The “path of least time” thing, however, frequently feels like more of a happy coincidence than a physical law.
As a counter example, consider a coherent laser beam that I fire into a material with a VERY high index of refraction (so it causes the laser to move extremely slowly). It would always make the time shorter if the laser beam somehow bent around the material instead of going through it. But it doesn’t, it flies straight ahead because that’s what lasers do.
Thus, the path of least time has always seemed like an odd condition that just happens to work in certain constructed circumstances.
Pingback: தமிழ இயல்பு: ஸ்னெல் ஒளித்தடம் + ஸிப்ஃப் மானுட இயல்புக் கோட்பாடுகள் | ஒத்திசைவு...
This might be a silly question, but why has the size of the wave front gotten bigger (stretched) as light traveled from one medium to the other?
The principle of least time at first seems strange to those accustomed to living in a three-dimensional Euclidean space whom usually experience only small relative velocities between objects in their surroundings (us), and thus don’t have a day-to-day experience of the four-dimensional space-time in which they actually live.
However, a photon very much lives in the four-dimensional Minowski space-time that we don’t usually experience, because it’s moving at the speed of light. As such, you would expect even slight disturbances in this fourth (time) dimension to have a real effect on the path of a photon through its four-dimensional Minowski space. Sending the photon along the shortest Euclidean path may be sort of be like ‘forcing’ the photon to go up a four-dimensional hill instead of around it.
This to my mind makes just as much intuitive sense as the way a planet ‘knows’ which path to fall along as it orbits around another body (which has caused the spacetime around it to become curved), without having to actually try all of the possible paths, in order to minimise its path through that curved space. In this case, we are noticing the curvature of space more than a curvature of time. So why should not a photon take the path that it does between two points in order to minimise the time that it takes? When you stick a piece of glass in a photon’s path, you’re altering its speed dramatically (as projected onto our reference frame). You’re altering significantly the space through which it travels, particularly in the photon’s time dimension.
That’s the analogy i like to make.
Hi,
thank you for an interesting post, which I have just stumbled upon.
I have a question ( – I realise that the post is a year old…):
In your wave-argument you have a drawing of a wave entering another material. This gives rise to 2 triangles.
1. The upper triangle is simply defined to be a “right triangle”.
2. The bottom triangle is drawn as also forming a 90 degree angle. Is this per assumption of the refraction, or can it somehow be inferred (without reference to Snell’s law, or the Principle of least action…)?
Could anyone please give me an expression for x?
referring to the first diagram
n=v1/v2
This means solving for x in
x^2/(a^2 +x^2)=(n^2*(c-x)^2)/((b^2 +(c-x)^2))
I really, really like that you give the two approaches back to back, for contrast. I am not a physicist—–just a teacher. I like to see things put in a manner described by Denzel Washington, in “Philadelphia” : “……I need you to explain the whole thing to me, as if I were a six yr old” No gross assumptions.
If you can clear up, for me, WHY you introduced the idea of dT/dx, right after drawing the triangles , it would help. I think I know, but still it would be good to see it. I understand what the derivative does, but how it plays into the greater derivaTION is the burning interest to me.
Sorry if I sound too elementary.
Thanks !
@rod reede
we figure out what values of x correspond with extreme values of T. Those x’s tell us which paths that takes the least or greatest amount of time. There’s no longest path, since you can just slide x to the right or left forever (to create arbitrarily long paths), so the one critical value of x is a minimum.
Thanks!
There are a lot of paths, and the only difference between them is the parameter x, the location where the path crosses through the surface. By setting
Alternatively, you could do it right and use a derivative test.
Hi,
Thanks for the intuitive explanation. In the wave case, the blue crest above the boundary appears shorter than that below the boundary. Shouldn’t they be the same (conservation of mass)? On the contrary, the requirement that every point of the wavefront refract at the same angle theta2 does imply that the before and after wavefronts be of different lenghts. I’m not sure how to interpret these seemingly contradictory requirements.
@Santosh Manicka
There is a conservation law at play here. When a wave becomes more spread out, whatever the context, its intensity drops. For example, when something makes a sound the wave fronts become bigger and bigger as the sound expands in all directions, but at the same time the sound becomes quieter.
What I don’t understand is that the curvature of space is proven by the assumption that light never curves, which now seems to be in question. I have always had concern for the proof of the the curvature of space, based on the basic assumption that any two masses have a gravitational attraction. And since light is photon flow, and a photon has a mass, how is that it is not affected to at least some degree by Newton’s law of universal gravitation.
It would seem only natural that if a photon was near a mass as large as a planet there would be some attraction, which would make the light curve.
@Denny Hayes – photons do not have mass. That’s why they travel at the speed of light. Only massless particles can accelerate to C. (using E = mc^2)
https://physics.stackexchange.com/questions/4700/why-cant-photons-have-a-mass
Cool! Many thanks for the nice explanation.
(Snell’s law should look familiar to anyone whose used to talking – should be “who’s used to …”)
@Richi
Thanks for catching that!
Pingback: Q: Why are the laws of quantum mechanics so strange? Does it mean that we’re missing something? | Ask a Mathematician / Ask a Physicist
Feynman explaination summary:
The light travel from A to B in evevy path but it intereferes to itself. According to path integral formulation, only the shortest path is not cancelled.
—
If we combine the classical view of light wave and qutumn. let’s assume the wave traval all the path from a to b, so that there’re many light paths and different position of the refraction points. We can draw a graph – path distance against the position of refraction. it looks like y = x^2
On the graph, the path distance change faster when it fars from the shortest path. it means the path difference is changing at those point. When you add many light with slightly different path difference, they eventually cancel out. Only the shortest path is remaining as the dy/dx = 0, at that point the path difference is zero.
Pingback: What’s Wrong With Shortcuts? (Ep. 483) - Freakonomics
Pingback: What’s Incorrect With Shortcuts? (Ep. 483) - Freakonomics - Tradenews
Pingback: What’s Wrong With Shortcuts? (Ep. 483) – Business News
Pingback: What’s Flawed With Shortcuts? (Ep. 483) - Freakonomics - Tradenews