Physicist: The chain rule is a tool from calculus that says that if you have one function “nested” inside of another, 
, then the derivative of the whole mess is given by 
. There are a number of ways to prove this, but one of the more enlightening ways to look at the chain rule (without rigorously proving it) is to look at what happens to any function, 
, when you muck about with the argument (the “x” part).
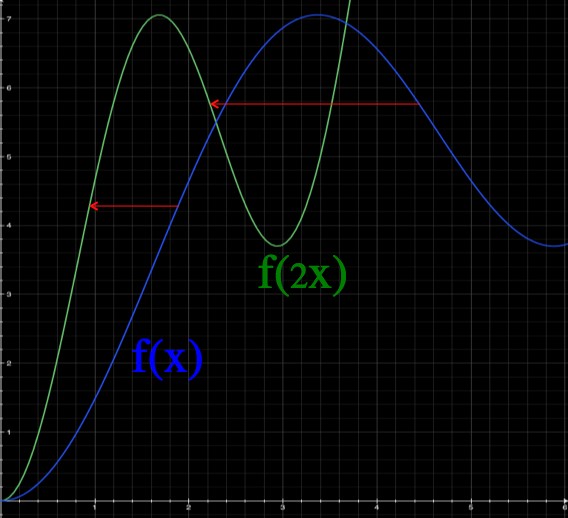
Doubling the "argument" of a function scrunches it up. As a result the slope at each corresponding part of the new function is doubled.
When you multiply the argument by some amount, the graph of the function gets squished by the same amount. If you, for example, plug in “x=3” to f(2x), that’s exactly the same as plugging in “x=6” to . For 
, everything happens at half the original x value.
However, while when x=3 is the same as when x=6, the same is not true of their slopes. The slope (derivative) is “rise over run” and the run just became half as long, so the slope just got twice as big. Scrunching a graph makes the slope steeper (see picture above).
So, the slope of at x=3 is actually double the slope of at x=6. You can write this in general as ![\frac{d}{dx} \left[ f(2x) \right] = \frac{df}{dx}(2x)\cdot 2](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdx%7D+%5Cleft%5B+f%282x%29+%5Cright%5D+%3D+%5Cfrac%7Bdf%7D%7Bdx%7D%282x%29%5Ccdot+2&bg=ffffff&fg=000000&s=0 "\frac{d}{dx} \left[ f(2x) \right] = \frac{df}{dx}(2x)\cdot 2")
.
Here’s the calculus leap: replacing the x in with 2x clearly means that you’re running through the function twice as fast, so when you take the derivative you just multiply by two to deal with the scrunching. But, if you instead replace x with a more complicated function, 
, then the amount of speed up and slow down depends on . If has a slope of 2 at some point, then it’s acting like 2x and you get the same “times two” slope. If it’s got a slope of 3 or 1/5, then the slope of 
at the corresponding point will be multiplied by 3 or 1/5 respectively.
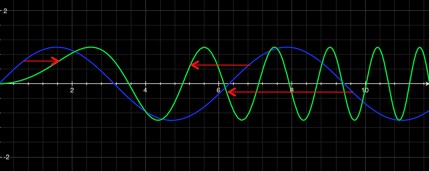
sin(x) in blue and sin(x^2/4) in green. x^2 starts slow and gets faster and faster, and as a result the green line gets steeper and steeper.
So, to find the slope of , which is just the derivative, ![\frac{d}{dx}\left[f(g(x))\right]](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5Bf%28g%28x%29%29%5Cright%5D&bg=ffffff&fg=000000&s=0 "\frac{d}{dx}\left[f(g(x))\right]")
you first find what the slope of would be at the appropriate x value, 
, and then multiply by how much 
is speeding things up or slowing things down (scrunching or expanding). The slope of is just the derivative, so you’re multiplying by 
.
Boom! Chain rule: ![\frac{d}{dx}\left[ f(g(x))\right] = \frac{df}{dx} (g(x))\cdot \frac{dg}{dx} (x)](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5B+f%28g%28x%29%29%5Cright%5D+%3D+%5Cfrac%7Bdf%7D%7Bdx%7D+%28g%28x%29%29%5Ccdot+%5Cfrac%7Bdg%7D%7Bdx%7D+%28x%29&bg=ffffff&fg=000000&s=0 "\frac{d}{dx}\left[ f(g(x))\right] = \frac{df}{dx} (g(x))\cdot \frac{dg}{dx} (x)")
It’s worth pointing out that, like all calc rules, it doesn’t matter that this rule only talks about two functions. If you have something like 
, then you can treat 
as one function, and you’ll find that after running through the chain rule once you’ll be faced with another, simpler, chain rule problem:
![\frac{d}{dx}\left[f(g(h(x)))\right] = \frac{df}{dx}(g(h(x)))\cdot\frac{d}{dx}\left[g(h(x))\right]](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5Bf%28g%28h%28x%29%29%29%5Cright%5D+%3D+%5Cfrac%7Bdf%7D%7Bdx%7D%28g%28h%28x%29%29%29%5Ccdot%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5Bg%28h%28x%29%29%5Cright%5D&bg=ffffff&fg=000000&s=0 "\frac{d}{dx}\left[f(g(h(x)))\right] = \frac{df}{dx}(g(h(x)))\cdot\frac{d}{dx}\left[g(h(x))\right]")
Very nice physical/geometric interpretation!
Is this a proof of the chain rule?:
Because dg(x)/dg(x) = 1 ,
[df(g(x))/dx] = [df(g(x))/dx] * 1 = [df(g(x))/dx] * [dg(x)/dg(x)] = [df(g(x)) * g(x)]/[dx * g(x)] = [df(g(x))/dg(x)] * [dg(x)/dx]
I know that infinitesimals can work funny sometimes but this seems very reasonable.
It’s a good thumbnail sketch but, as you say, infinitesimals work funny sometimes. For example, the proof here (and in the post) breaks down when multi-variable functions are considered.
That was unequivocally brilliant.
I made a video tutorial that might be useful (see the segment from 11m04s to 14m43s):
Best,
DL (lookatphysics.com)
I Really Needed The Proof’s Like This!
Not The Booring Proofs In My Text Books!
This Is What A Student Who Needs If He Needs To Study Mathematics Conceptually!
Thank’s!
It Gives The Clear Idea!
Pingback: TWSB: Back on the Chain Gang « Eigenblogger
This is awesome!! My thanks to The Physicist
Hi everyone- first let me just say how much I enjoy this website. I’ve found many wonderful, creative, and intuitive explanations on here that have helped me.
I actually found this post after pondering this question myself for the last several days. I realized that while I could easily “prove” the chain rule, I had no intuitive understanding of it. After several days I finally got that intuitive understanding I was looking for. I then Googled it to see what others had come up with and that’s how I ended up here. I really like your approach and it has added to my own understanding. If you’re interested, here’s what I had come up with before finding this post:
When I compose f(x) and g(x) I am, to use your words, “mucking” about with the inputs of f(x). If I leave the inputs alone, then f ‘(x) would describe the rate of change in the function values. I like to picture the inputs (the x-axis) as sitting on a stationary treadmill. As long as the treadmill doesn’t move, the function is just f(x) with a rate of change of f ‘(x). BUT, if I start running the treadmill, now the treadmill is introducing a rate of change to the INPUTS of my function. If we call the values of this “moving” x-axis g(x), then the x-axis values are “changing” at a rate = g ‘(x) BEFORE f(x) gets to act on them. Since the values of f(x) will already change at a rate of f ‘(x), and the inputs to the function are now changing at their own rate g'(x), then f ‘(g(x)) represents the rate of change f(x) brings to the table, and we need to multiply that by g ‘(x), the rate at which the inputs (x-axis values, the “treadmill”) are changing.
Thus we obtain that the rate of change of f(g(x)) = f ‘(g(x))*g ‘(x)
What do you think?
I think that’s a solid way to think of it!
Thank you very much for this. I’d been trying to figure out what was wrong with my understanding of the chain rule, wracking my brains for the past day or two, and this cleared it right up. In particular, I’d forgotten that the squishing/stretching would be different in different regions.
Pingback: TWSB: Back on the Chain Gang | Eigenblogger