Physicist: There’d definitely still be a horizon if the Earth were flat. It would be in almost exactly the same place, and look essentially identical. While the Earth isn’t flat, adherents to that theory are correct in that it’s nearly so, and if you’re standing on the surface of a round something the size of the Earth it’s difficult to tell the difference (in fact, mathematically you can make the argument that a flat Earth acts the same as an infinitely big Earth).
For someone around 5’6″ tall, if the Earth were perfectly flat the horizon would be about 0.04° higher. That’s about the width of a (mechanical) pencil lead held at arm’s length. Unless you have short arms, in which case you’ll need to shave down the lead a little.
Even if the Earth were perfectly flat and went on forever, the horizon would still be exactly level: 180° of sky and 180° of ground (instead of the paltry 179.92° of ground we have). The only difference between a finite flat Earth and an infinite flat Earth is that no matter how tall you are on an infinite flat Earth, the horizon always stays in the same place.
However, even though the horizon of an infinite and flat Earth might actually be in the same place, it wouldn’t appear to be. An infinite plane has an extremely simple gravitational field; uniform and exactly the same regardless of distance. Normally the higher you are the weaker the gravity, but for a flat Earth that isn’t the case.
As such, light, which drops only imperceptibly under Earth’s gravity, has an infinitely great distance over which to do its dropping. The effect would require tremendous distances (as in; interstellar distances), but if you’ve got an infinite plane, that kind of distance is cheap.
Given enough time and distance light will eventually curve back toward an infinite plane of matter. So if you’re standing somewhere on the surface and you look up you’ll see light that started somewhere else on the surface. Instead of a horizon, the world would look like it rises up on all sides and encloses you.
When you look up from what should be the horizon you’ll just see more of the infinite-flat-Earth. The one exception is what you’d see if you looked straight up. Directly above you you’d find the entire horizon bunched up at that point.
Answer gravy: It’s not interesting enough to include in the post directly, but here’s how the math above was done:
If you’re standing on a sphere with radius R and you’re H tall, then the distance from your head to the middle of the sphere is R+H. Your line of sight to the horizon is a tangent line to the sphere. This allows you to draw a right triangle and do a little trigonometry.
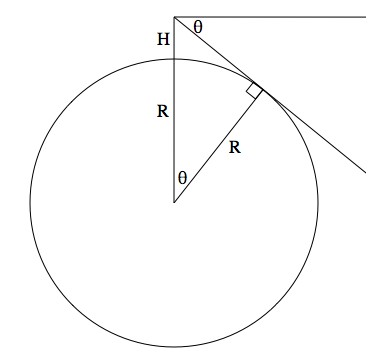
θ is the angle between the “true horizon” and the perfectly level “ideal horizon”. Coincidentally, it’s also the angle between where you’re standing on a sphere and the farthest thing you can see on the surface.
So, and
. Plug in R = 6,378,100 meters and H = 1.68 meters (which is 5’6″), and you find that θ = 0.04°.
By the end of college, electrical engineers and physicists get sick to death of the example of the infinite plane of anything (be it matter, electrical charge, kittens, whatnot). The reason an infinite plane is useful is that it has some nice symmetry. You can argue that, since no direction is special (by being close to an edge for example) gravity always points straight into or out of the plane-o-stuff. Symmetry is useful when you use a Gaussian surface, because you can ignore buckets of math.
Basically, draw a “bubble” around a lump of matter. The total gravitational field pointing through that bubble will be proportional to the amount of matter inside. So, the more matter, the more gravity. The bigger the bubble, the less the strength of the field through any particular part of the surface (by the by, there’s an example of this in action here). If the Gaussian surface you choose is a rectangular box that punches through the flat-Earth, then you find that it doesn’t matter how tall the box is.
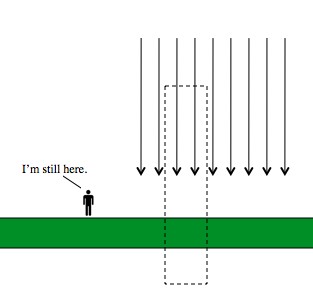
The total amount of gravity pointing into any imaginary box you can draw is always proportional to the amount of matter in that box. In this case, no gravity points through the sides (by symmetry) so it all points through the top. But if you make the box taller that doesn’t change. As a result, for an infinite plane gravity stays the same forever. QED y’all!
Uniform and infinite sheets of matter or charge have gravitational or electric fields that extend, without changing, forever. Of course, there are barely any infinite planes of stuff out there, so this isn’t a situation that ever actually comes up. However! If you’re close enough to a surface it can seem to be nearly infinite, so the infinite-plane solutions are often good enough.
And often as not, “good enough” is good enough for physics.








74 Responses to Q: If Earth was flat, would there be a horizon? If so, what would it look like? If the Earth was flat and had infinite area, would that change the answer?