Q: What is quantum teleportation? Why can’t we use it to communicate faster than light?

Physicist: Contrary to its exciting name, quantum teleportation doesn’t involve any physical stuff suddenly disappearing and then reappearing somewhere else.  Instead it’s a cute, clever, technique for transferring an unknown quantum state of one system (usually a single particle) to another, specially prepared, system.  That sounds a lot cooler and more interesting than the reality.  Before even getting into quantum teleportation, I’ll describe how to do “classical teleportation”, and you can judge whether “teleport” is even the appropriate word.  This is great at parties (or, more likely, Dr. Who marathons at your mom’s house)!

Classical teleportation:

i) Get three coins (hereafter called A, B , and C), and set up B and C to be the same side up (but which side is up should be completely random).

ii) Flip A.

iii) Compare A and B.  If they’re the same, then leave C alone.  If they’re different, then turn C over.

iv) What was the heads/tails state of A is now the state of C.

B and C start the same. If A and B are the same, then C and A are already the same. If A and B are different, then flipping C will make A and C the same.  This works independently of the heads/tails configurations (as long as B and C start the same), so you don’t even need to know what faces are up.

What’s deeply spooky about this is that you can set it up so that the state of A is transmitted to C, without ever knowing what the states of any of the coins are.  In step one make B and C the same, then while holding them together, turn them over several times until you’ve lost track of how many times you’ve done it, then cover them.  They’ll be the same, but you won’t know which side they both have up.  Do the same sort of thing in step three: bring A and B together, turn them over several times, then see if they’re the same or different.

Or just get someone else to do it for you.

The “teleportation” comes in because you can move C as far away as you like.  Once you compare A and B you can then shout (or, for a long distance teleport, call on the phone) “same” or “different”, and whoever has C can leave it alone or flip it over.  The unknown state of A has been teleported to C.  Notice that, until you tell C’s owner about the result of the same/different measurement, the state of C has absolutely nothing to do with the state of A.  This is the big limitation of teleportation and why it isn’t faster than light; you have to communicate the results of the measurement, and that communication is through ordinary, not-faster-than-light channels.  Without that communication C remains random and has nothing to do with A.

Whether or not this trick qualifies as remarkable, or even deserves the moniker “teleportation”, is a matter of personal preference.  That said, this brand of teleportation can send physical objects from place to place exactly as effectively as an email can.

Quantum teleportation is not this. Not this at all.

Quantum teleportation has the same limitations and works very similarly.

Answer gravy: And here’s how.  There are several teleportation schemes and, believe it or not, this is the simplest.

The basic idea is the same as the coin trick; you start with two particles, B and C, that are entangled.  Then you bring in particle A that’s in an unknown state and compare it to B (in a way that doesn’t involve directly measuring the states of either).  Then the results of that comparison are communicated, and C is altered.

A “qubit“, is like a regular “bit” (or a coin), except that instead of just 0 or 1 (heads or tails) it can be in a combination of both.  What is physically meant by 1 or 0, or how a qubit is manipulated, depend on the system involved.  It could be electron spins manipulated by magnets, or photon paths manipulated by beam splitters, or a dozen other things.  Doesn’t really matter.

The notation here is a little tricky, but stay with me.  In what follows “” is the notation for a state of all three qubits.  So, for example, is the state A=1, B=0, and C=1.  In quantum mechanics things can be in more than one state at once.  For example, B and C will start in the entangled state , which means that they’re in a 50/50 combination of “both zero” and “both one”.

That √2 is there because when you actually do a measurement, the probability of finding a particular state is the coefficient squared.  This is called the “Born Rule“, and don’t worry about it.  Those √2’s are mostly just clutter.

How to quantum teleport the state of A onto C.

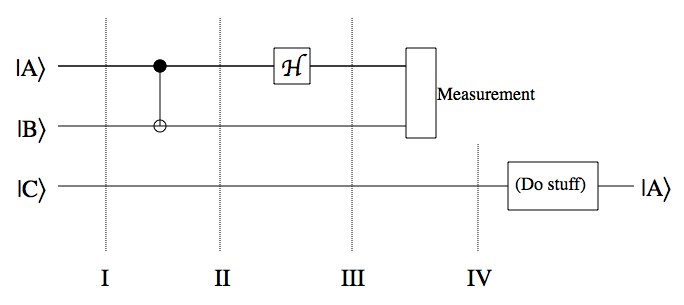
The initial state of all three qubits, “I” in the picture above, is:

Where the state of A, , which is the state to be teleported, is completely unknown (α and β are unknown).  The first thing that’s done is a “Controlled Not Gate”.  An ordinary Not Gate flips the bit, and .  But a Controlled Not has a “control bit” and a “target bit”.  If the control bit is 0, then nothing happens, and if the control bit is 1, then the target bit is flipped.  In this case, A is the control bit and B is the target.  This interaction makes the state of A and the state of B entangled.  After the Controlled Not the state of the three qubits, “II” in the picture above, is:

Notice that after the CNot gate the qubits can no longer be factored apart, the way the state at I could be factored.  This is symptomatic of entangled systems.  Next comes the “Hadamard Gate”, which only exists for quantum systems.  CNot gates can be done in a regular computer, but the Hadamard Gate is all quantum, baby.  Here’s what it does: and .  This step is hides what state A started out as, so when a measurement is done (in a moment) you don’t directly measure A.  This is important, because if you measure a state it collapses*.  So instead of having , you’re left with just or just , which are different from A.  After applying the Hadamard Gate to A, the state of the three qubits, “III” in the picture above, is:

This can be rearranged a bit,

Now when A and B are measured, they can have one of four possible results, 00, 01, 10, and 11.  When a measurement is made, then what remains are all of those states consistent with the measurement.  For example, if A is measured to be 1, then the state remaining is , and if B is then found to be 0, then the state remaining is .

Each of the four results will mean that C is left in one of four states:

If the person in charge of C (the Custodian?) is then told the results, no matter how far away they are, they can perform some basic fixes.  For example, if the result is 00, then they leave the state alone.  If the result is 01, they run C through a Not gate (which switches 0 and 1).  For the others a “Phase Gate” (another quantum-only kind of logic gate) is used, which takes and .

Here’s the important bit.  Just like the “classical teleportation” above, without knowledge of what the results of the AB measurement were, the person in charge of C (the Controller?) can’t turn C into the original A state.  If they were to measure C, without doing any of the fixes, they’d find that the probability of getting a zero or a one is exactly 50%, instead of |α|² and |β|² which it should be (again, by the Born rule).  Each of the four measurements are equally likely, and the chance of getting a “1” is the sum of chances from each state: 0.25(|β|²+|α|²+|β|²+|-α|²) = 0.25(1+1) = 0.5 (since |β|²+|α|²=1).

You may suspect that there’d be some way to manipulate C, without getting the results of the measurement, that would allow you to overcome this lack of information.  Turns out: nope.  It’s much harder to see why, and it dips into quantum information theory, but the proof is fairly “straightforward”.  This is just for those of you who really feel like looking this stuff up, so it’ll be fast.

The “probability density matrix” for C, before any information is received, is or one half times the identity matrix (those halves are the 50/50 probabilities from a moment ago).  You can figure this out by “tracing out” all of the unknown components (A and B).  Everything that you can do to the state C, including all of the stuff mentioned earlier like Not gates, and Hadamard Gates, and whatnot, amounts to a coordinate change on the probability density matrix.  But since it’s essentially just the identity matrix, none of them change anything.  The α’s and β’s of the original state never show up in C (not even a little) before the results of the measurement (00, 01, 10, or 11) are communicated.

So once again, without ordinary communication, nothing about A is conveyed to C, and if you only had access to C, you’d never know that a measurement was even done.

*Not really.  When quantum systems interact they become entangled.  From inside of a system this looks like “wave function collapse” which causes no end of paradoxes and problems, but from outside of the systems involved interactions don’t cause collapses, just entanglement.  There’s a whole post about this brain trip here.