Q: Why are determinants defined the weird way they are?

Posted on May 6, 2013 by The Physicist

Physicist: This is a question that comes up a lot when you’re first studying linear algebra. The determinant has a lot of tremendously useful properties, but it’s a weird operation. You start with a matrix, take one number from every column and multiply them together, then do that in every possible combination, and half of the time you subtract, and there doesn’t seem to be any rhyme or reason why. This particular math post will be a little math heavy.

If you have a matrix, ${\bf M} = \left(\begin{array}{cccc}a_{11} & a_{21} & \cdots & a_{n1} \\a_{12} & a_{22} & \cdots & a_{n2} \\\vdots & \vdots & \ddots & \vdots \\a_{1n} & a_{2n} & \cdots & a_{nn}\end{array}\right)$ , then the determinant is $det({\bf M}) = \sum_{\vec{p}}\sigma(\vec{p}) a_{1p_1}a_{2p_2}\cdots a_{np_n}$ , where $\vec{p} = (p_1, p_2, \cdots, p_n)$ is a rearrangement of the numbers 1 through n, and $\sigma(\vec{p})$ is the “signature” or “parity” of that arrangement. The signature is (-1)^k, where k is the number of times that pairs of numbers in $\vec{p}$ have to be switched to get to $\vec{p} = (1,2,\cdots,n)$ .

For example, if ${\bf M} = \left(\begin{array}{ccc}a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\a_{13} & a_{23} & a_{33} \\\end{array}\right) = \left(\begin{array}{ccc}4 & 2 & 1 \\2 & 7 & 3 \\5 & 2 & 2 \\\end{array}\right)$ , then

$\begin{array}{ll}det({\bf M}) \\= \sum_{\vec{p}}\sigma(\vec{p}) a_{1p_1}a_{2p_2}a_{3p_3} \\=\left\{\begin{array}{ll}\sigma(1,2,3)a_{11}a_{22}a_{33}+\sigma(1,3,2)a_{11}a_{23}a_{32}+\sigma(2,1,3)a_{12}a_{21}a_{33}\\+\sigma(2,3,1)a_{12}a_{23}a_{31}+\sigma(3,1,2)a_{13}a_{21}a_{32}+\sigma(3,2,1)a_{13}a_{22}a_{31}\end{array}\right.\\=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}\\= 4 \cdot 7 \cdot 2 - 4 \cdot 2 \cdot 3 - 2 \cdot 2 \cdot 2 +2 \cdot 2 \cdot 1 + 5 \cdot 2 \cdot 3 - 5 \cdot 7 \cdot 1\\=23\end{array}$

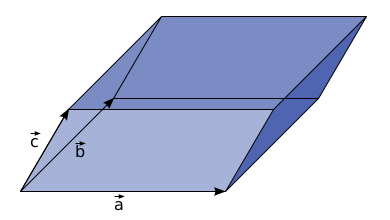
Turns out (and this is the answer to the question) that the determinant of a matrix can be thought of as the volume of the parallelepiped created by the vectors that are columns of that matrix. In the last example, these vectors are $\vec{v}_1 = \left(\begin{array}{c}4\\2\\5\end{array}\right)$ , $\vec{v}_2 = \left(\begin{array}{c}2\\7\\2\end{array}\right)$ , and $\vec{v}_3 = \left(\begin{array}{c}1\\3\\2\end{array}\right)$ .

The parallelepiped created by the vectors a, b, and c.

Say the volume of the parallelepiped created by $\vec{v}_1, \cdots,\vec{v}_n$ is given by $D\left(\vec{v}_1, \cdots, \vec{v}_n\right)$ . Here come some properties:

1) $D\left(\vec{v}_1, \cdots, \vec{v}_n\right)=0$ , if any pair of the vectors are the same, because that corresponds to the parallelepiped being flat.

2) $D\left(a\vec{v}_1,\cdots, \vec{v}_n\right)=aD\left(\vec{v}_1,\cdots,\vec{v}_n\right)$ , which is just a fancy math way of saying that doubling the length of any of the sides doubles the volume. This also means that the determinant is linear (in each column).

3) $D\left(\vec{v}_1+\vec{w},\cdots, \vec{v}_n\right) = D\left(\vec{v}_1,\cdots, \vec{v}_n\right) + D\left(\vec{w},\cdots, \vec{v}_n\right)$ , which means “linear”. This works the same for all of the vectors in $D$ .

Check this out! By using these properties we can see that switching two vectors in the determinant swaps the sign.

$\begin{array}{ll} D\left(\vec{v}_1,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)\\ =D\left(\vec{v}_1,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)+D\left(\vec{v}_1,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 1}\\ =D\left(\vec{v}_1,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 3} \\ =D\left(\vec{v}_1,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)-D\left(\vec{v}_1+\vec{v}_2,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 1} \\ =D\left(-\vec{v}_2,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 3} \\ =-D\left(\vec{v}_2,\vec{v}_1+\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 2} \\ =-D\left(\vec{v}_2,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right)-D\left(\vec{v}_2,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 3} \\ =-D\left(\vec{v}_2,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right) & \textrm{Prop. 1} \end{array}$

4) $D\left(\vec{v}_1,\vec{v}_2, \vec{v}_3\cdots, \vec{v}_n\right)=-D\left(\vec{v}_2,\vec{v}_1, \vec{v}_3\cdots, \vec{v}_n\right)$ , so switching two of the vectors flips the sign. This is true for any pair of vectors in D. Another way to think about this property is to say that when you exchange two directions you turn the parallelepiped inside-out.

Finally, if $\vec{e}_1 = \left(\begin{array}{c}1\\0\\\vdots\\0\end{array}\right)$ , $\vec{e}_2 = \left(\begin{array}{c}0\\1\\\vdots\\0\end{array}\right)$ , … $\vec{e}_n = \left(\begin{array}{c}0\\0\\\vdots\\1\end{array}\right)$ , then

5) $D\left(\vec{e}_1,\vec{e}_2, \vec{e}_3\cdots, \vec{e}_n\right) = 1$ , because a 1 by 1 by 1 by … box has a volume of 1.

Also notice that, for example, $\vec{v}_2 = \left(\begin{array}{c}v_{21}\\v_{22}\\\vdots\\v_{2n}\end{array}\right) = \left(\begin{array}{c}v_{21}\\0\\\vdots\\0\end{array}\right)+\left(\begin{array}{c}0\\v_{22}\\\vdots\\0\end{array}\right)+\cdots+\left(\begin{array}{c}0\\0\\\vdots\\v_{2n}\end{array}\right) = v_{21}\vec{e}_1+v_{22}\vec{e}_2+\cdots+v_{2n}\vec{e}_n$

Finally, with all of that math in place,

$\begin{array}{ll} D\left(\vec{v}_1,\vec{v}_2, \cdots, \vec{v}_n\right) \\ = D\left(v_{11}\vec{e}_1+v_{12}\vec{e}_2+\cdots+v_{1n}\vec{e}_n,\vec{v}_2, \cdots, \vec{v}_n\right) \\ = D\left(v_{11}\vec{e}_1,\vec{v}_2, \cdots, \vec{v}_n\right) + D\left(v_{12}\vec{e}_2,\vec{v}_2, \cdots, \vec{v}_n\right) + \cdot + D\left(v_{1n}\vec{e}_n,\vec{v}_2, \cdots, \vec{v}_n\right) \\= v_{11}D\left(\vec{e}_1,\vec{v}_2, \cdots, \vec{v}_n\right) + v_{12}D\left(\vec{e}_2,\vec{v}_2, \cdots, \vec{v}_n\right) + \cdot + v_{1n}D\left(\vec{e}_n,\vec{v}_2, \cdots, \vec{v}_n\right) \\ =\sum_{j=1}^n v_{1j}D\left(\vec{e}_j,\vec{v}_2, \cdots, \vec{v}_n\right) \end{array}$

Doing the same thing to the second part of D,

$=\sum_{j=1}^n\sum_{k=1}^n v_{1j}v_{2k}D\left(\vec{e}_j,\vec{e}_k, \cdots, \vec{v}_n\right)$

The same thing can be done to all of the vectors in D. But rather than writing n different summations we can write, $=\sum_{\vec{p}}\, v_{1p_1}v_{2p_2}\cdots v_{np_n}D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right)$ , where every term in $\vec{p} = \left(\begin{array}{c}p_1\\p_2\\\vdots\\p_n\end{array}\right)$ runs from 1 to n.

When the $\vec{e}_j$ that are left in D are the same, then D=0. This means that the only non-zero terms left in the summation are rearrangements, where the elements of $\vec{p}$ are each a number from 1 to n, with no repeats.

All but one of the $D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right)$ will be in a weird order. Switching the order in D can flip sign, and this sign is given by the signature, $\sigma(\vec{p})$ . So, $D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right) = \sigma(\vec{p})D\left(\vec{e}_{1},\vec{e}_{2}, \cdots, \vec{e}_{n}\right)$ , where $\sigma(\vec{p})=(-1)^k$ , where k is the number of times that the e’s have to be switched to get to $D(\vec{e}_1, \cdots,\vec{e}_n)$ .

So,

$\begin{array}{ll} det({\bf M})\\ = D\left(\vec{v}_{1},\vec{v}_{2}, \cdots, \vec{v}_{n}\right)\\ =\sum_{\vec{p}}\, v_{1p_1}v_{2p_2}\cdots v_{np_n}D\left(\vec{e}_{p_1},\vec{e}_{p_2}, \cdots, \vec{e}_{p_n}\right) \\ =\sum_{\vec{p}}\, v_{1p_1}v_{2p_2}\cdots v_{np_n}\sigma(\vec{p})D\left(\vec{e}_{1},\vec{e}_{2}, \cdots, \vec{e}_{n}\right) \\ =\sum_{\vec{p}}\, \sigma(\vec{p})v_{1p_1}v_{2p_2}\cdots v_{np_n} \end{array}$

Which is exactly the definition of the determinant! The other uses for the determinant, from finding eigenvectors and eigenvalues, to determining if a set of vectors are linearly independent or not, to handling the coordinates in complicated integrals, all come from defining the determinant as the volume of the parallelepiped created from the columns of the matrix. It’s just not always exactly obvious how.

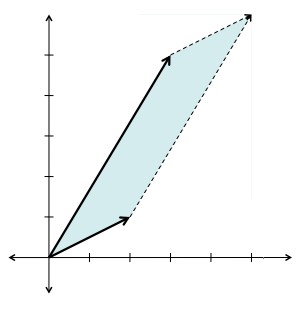
For example: The determinant of the matrix ${\bf M} = \left(\begin{array}{cc}2&3\\1&5\end{array}\right)$ is the same as the area of this parallelogram, by definition.

The parallelepiped (in this case a 2-d parallelogram) created by (2,1) and (3,5).

Using the tricks defined in the post:

$\begin{array}{ll} D\left(\left(\begin{array}{c}2\\1\end{array}\right),\left(\begin{array}{c}3\\5\end{array}\right)\right) \\[2mm] = D\left(2\vec{e}_1+\vec{e}_2,3\vec{e}_1+5\vec{e}_2\right) \\[2mm] = D\left(2\vec{e}_1,3\vec{e}_1+5\vec{e}_2\right) + D\left(\vec{e}_2,3\vec{e}_1+5\vec{e}_2\right) \\[2mm] = D\left(2\vec{e}_1,3\vec{e}_1\right) + D\left(2\vec{e}_1,5\vec{e}_2\right) + D\left(\vec{e}_2,3\vec{e}_1\right) + D\left(\vec{e}_2,5\vec{e}_2\right) \\[2mm] = 2\cdot3D\left(\vec{e}_1,\vec{e}_1\right) + 2\cdot5D\left(\vec{e}_1,\vec{e}_2\right) + 3D\left(\vec{e}_2,\vec{e}_1\right) + 5D\left(\vec{e}_2,\vec{e}_2\right) \\[2mm] = 0 + 2\cdot5D\left(\vec{e}_1,\vec{e}_2\right) + 3D\left(\vec{e}_2,\vec{e}_1\right) + 0 \\[2mm] = 2\cdot5D\left(\vec{e}_1,\vec{e}_2\right) - 3D\left(\vec{e}_1,\vec{e}_2\right) \\[2mm] = 2\cdot5 - 3 \\[2mm] =7 \end{array}$

Or, using the usual determinant-finding-technique, $det\left|\begin{array}{cc}2&3\\1&5\end{array}\right| = 2\cdot5 - 3\cdot1 = 7$ .

This entry was posted in -- By the Physicist, Math. Bookmark the permalink.

18 Responses to Q: Why are determinants defined the weird way they are?

Flavian Popa says:

May 7, 2013 at 3:43 am

Many thanks for the posting, you certainly do a great job explaining key mathematical concepts to people! And in a relaxed round-about way!
Eric says:

May 8, 2013 at 8:48 pm

What does swapping two of the vectors correspond to in the geometric interpretation? If I put all the vectors with their tail at the origin, the order in which I put them there shouldn’t make any difference in the volume of the parallelpiped formed. It wouldn’t turn it inside-out.
Error: Unable to create directory uploads/2024/12. Is its parent directory writable by the server? The Physicist says:

May 8, 2013 at 9:41 pm

The idea of a “negative volume” is important for linearity to make sense. That is, if $D(a\vec{e}_1, \cdots,\vec{e}_n) = aD(\vec{e}_1, \cdots,\vec{e}_n)$ , and $a$ can be negative, then the volume must have the option of being negative (being “inside out”).
Swapping vectors is the same as a reflection over the plane between them. For example, switching the x and y coordinates is exactly the same as reflecting over the line/plane x=y.
The positiveness/negativeness is described by parity, which (weirdly) does depend on the order of the vectors.
Rigney says:

May 9, 2013 at 7:58 am

Sorry that my question has nothing to do with algebra, but the following link is quite interesting to me. I wonder if it is theory or fantasy? Perhaps you might give me your opinion and thoughts on this 3 part hypothetical? Thanks
Flo says:

May 10, 2013 at 2:50 am

What is the mathematician up to these days? I haven’t read anything by him in quite a while.
Neal says:

May 11, 2013 at 4:19 pm

I think it’s worth pointing out that there’s a nice, clean, coordinate-free way to understand the determinant. If $V$ is a real vector space, the top exterior power is a one-dimensional real vector space $\Lambda^n V$ . A self-map $M:V\to V$ induces a map $V^*:\Lambda^nV\to\Lambda^nV$ . Since $\Lambda^nV$ is a one-dimensional real vector space, $V^*$ is multiplication by some real number. That number is (you guessed it) the determinant of $V$ .
Pingback: Carnival of Mathematics #99 « Wild About Math!
multivector says:

June 5, 2013 at 1:53 pm

A good reference for understanding the patterns of the determinant come from Geometric Algebra, (See Linear and Geometric Algebra by Macdonald). In essence, it’s the outer product of all of the vectors of the matrix.
Bill says:

June 5, 2013 at 10:40 pm

In the first figure, is the a[n,1] intended to appear in M twice? It appears to be a copy paste error.
Error: Unable to create directory uploads/2024/12. Is its parent directory writable by the server? The Physicist says:

June 5, 2013 at 11:19 pm

It is definitely not supposed to appear twice. Fixed!
Pingback: TWSB: We’re In the Matrix | Eigenblogger
Aneps says:

September 25, 2013 at 3:56 am

It was a nice explanation. But you mostly explained based on a 3X3 matrix! I have a few questions.
1)What is the physical significance of 4X4 and higher matrices? What is the use/any physical examples for 4×4 and higher order matrices?
2)Is there any physical significance for “Non Square” matrices?
3)What is the physical meaning of “Rank of a Matrix”?
Tom says:

April 23, 2014 at 6:55 pm

Great article, thanks! I truly appreciate that you explain where the idea could come from.
I really liked your way of thinking about negative volume (when one additionaly heard about base orientation and that ||two bases give the same sign of determinant if and only if there exists a continous family of bases containing these two bases|| it really lets you grasp the intuition).
It took me a while to feel the linearity of volume. (easy to see in 2D, not so obvious in 3D), a picture for that would make your work yet better.
Pingback: TWSB: We’re In the Matrix | Eigenblogger
Chris Austin says:

September 17, 2015 at 4:54 pm

Thanks a lot! Really helped me understand the determinant 🙂
Ed says:

March 7, 2016 at 8:16 pm

It’s really an excellent explanation! Thank you so much!
But I still have a question. How is property 3) true? I mean I know it’s linear, but in the sense of “volume”, it’s not so obvious and it can be confusing.
D says:

July 19, 2016 at 2:24 am

@ Ed:

The easiest way to see property 3 is probably to move the vector combination in question from the first column to the last column. Also in the interest of expediency I will only consider the absolute value of the determinant (e.g. a determinant of +7 and -7 are the same for my purposes here).

Like most things involving matrices, orthogonality allows you to quickly cut to the issue.

So, first QR factorize A. So $A = QR$ . Note when multiplying two matrices, say A and B, det(AB) = det(A)det(B).

So if we do $R = Q^T (QR)= Q^T A$ , then $det(R) = det(Q^T)det(A)$ . Note that Q and its transpose are orthonormal, and so they have a determinant of 1.

The eigenvalues of R will be quite different from A, but $det(R) = det(Q^T)det(A) = 1 * det(A)$ . And R is triangular so each of its diagonal elements is a eigenvalue. The determinant is, then, the product of those diagonal elements. Further if before factorizing, you had split out that final column vector into a separate w component and separate v, the question would be, is separate v linearly independent from the rest of the column in the matrix it is in? If it is, then we can see it’s contribution to the determinant via the bottom right corner entry in R. Similar question with w. Note that if either or both v and w are not linearly dependent, then the associated value in the bottom right cell of ‘their R’ is 0, and hence the associated determinant is zero.

Conclusion: if the product of the all eigenvalues but the last one in the bottom right is P, then v’s contribution * P + w’s contribution * P = (v’s contribution + w’s contribution)*P. That is the linear combination mentioned in property number 3.
Anonymous says:

December 24, 2020 at 10:55 pm

What is means of rank in matrix