Physicist: This question usually comes in the form of “are complex numbers real?” or “are negative numbers real?” or something along those lines. Turns out you can answer all of these questions at once (if you make up a nice enough definition for what “real” means).
If you think of “realness” in terms of what can be touched, or observed, or measured, then numbers (all kinds of numbers) are clearly not real. That is, numbers don’t phyiscally exist anywhere. No beachcomber will ever discover a new number during the practice of their venerated craft. That said, many people would say that “natural numbers” (which are 1, 2, 3, …) are real in the sense that you can find examples in nature of 3, because you can see (for example) 3 turtles together. Hence the name: natural numbers. By the same note, imaginary numbers don’t exist, because you’ll never see turtles (where
) in nature.
Numbers (math in general really) are all about describing patterns. Regular numbers are great at describing some things (like how many turtles are around), but there are a lot of patterns in nature that can’t be so easily described and require different kinds of “mathematical objects”, like negative numbers, non-integer numbers, complex numbers, matrices, polynomials, lots of stuff.
“3” seems to be a nice and solid property of the group of turtles in the picture above, and “3” seems pretty “real” as a result. You can move the turtles around, rename them, paint them, whatever, and you’ll still have 3. But there’s nothing terribly special about the property of having a certain number of things. Something like a knot, for example, has properties that are very real but are better described by polynomials. The “Alexander-Conway polynomial of a knot” stays the same no matter how you change the knot (any change that doesn’t involve cutting).
By the way, this isn’t particularly advanced math and you can learn it yourself!
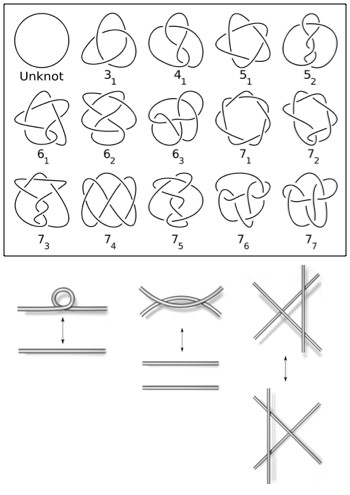
All of the simplest knots, expressed with the least number of crossings, and the “Reidemeister moves” which change what a knot looks like, but don’t actually change the knot itself. Each of these knots (and a lot more) have their own polynomial.
So (and this is the answer), if things in math are “real” because they describe simple properties of things we can see, then natural numbers are no more or less real than polynomials. The same kind of argument can (probably) be made for all of the other weird structures in mathematics. It’s just that the number of turtles is a much more obvious property than, say, the topology of a turtle’s plumbing (polynomials or lists of numbers), or its age (real numbers), or its ancestry (graphs). The quantum mechanical wave function of a turtle (or anything else) is described using complex numbers, because trying to do quantum mechanics without complex numbers is practically impossible. About as hard as counting turtles without the (obviously “real”) natural numbers.
The turtle picture is from here.








11 Responses to Q: Are numbers real?