Q: How do you define the derivatives of the Heaviside, Sign, Absolute Value, and Delta functions? How do they relate to one another?

Physicist: These are four standard reference functions.  In the same way that there are named mathematical constants, like π or e, there are named mathematical functions.  These are among the more famous (after the spotlight hogging trig functions).

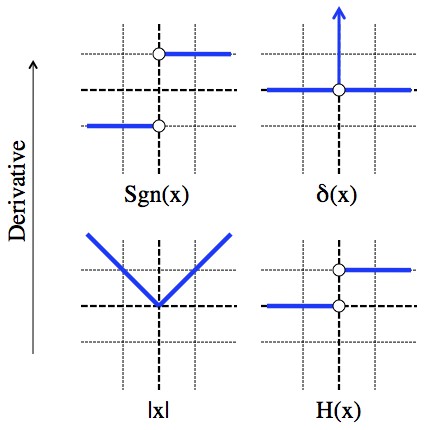
The Sign, Delta, Absolute Value, and Heaviside functions.  The graphs on top are the slope of the graphs on the bottom (and slope=derivative).

The absolute value function flips the sign of negative numbers, and leaves positive numbers alone.  The sign function is 1 for positive numbers and -1 for negative numbers.  The Heaviside function is very similar; 1 for positive numbers and 0 for negative numbers.  By the way, the Heaviside function, rather than being named after its shape, is named after Oliver Heaviside, who was awesome.

The delta function is a whole other thing.  The delta function is zero everywhere other than at x=0 and at x=0 it’s infinite but there’s “one unit of area” under that spike.  Technically the delta function isn’t a function because it can’t be defined at zero.  The “Dirac delta function” is used a lot in physics (Dirac was a physicist) to do things like describe the location of the charge of single particles.  An electron has one unit of charge, but it’s smaller than basically anything, so describing it as a unit of charge located in exactly one point usually works fine (and if it doesn’t, don’t use a delta function).  This turns out to be a lot easier than modeling a particle as… just about anything else.

The derivative of a function is the slope of that function.  So, the derivative of |x| is 1 for positive numbers (45° up), and -1 for negative numbers (45° down).  But that’s the sign function!  Notice that at x=0, |x| has a kink and the slope can’t be defined (hence the open circles in the graph of sgn(x)).

The derivative of the Heaviside function is clearly zero for x≠0 (it’s completely level), but weird stuff happens at x=0.  There, if you were to insist that somehow the slope exists, you would find that no finite number does the job (vertical lines are “infinitely steep”).  But that sounds a bit like the delta function; zero everywhere, except for an infinite spike at x=0.

It is possible (even useful!) to define the delta function as δ(x) = H'(x).  Using that, you find that sgn'(x) = 2δ(x), simply because the jump is twice the size.  However, how you define derivatives for discontinuous functions is a whole thing, so that’ll be left in the answer gravy.

Answer Gravy: The Dirac delta function really got under the skin of a lot of mathematicians.  Many of them flatly refuse to even call it a “function” (since technically it doesn’t meet all the requirements).  Math folk are a skittish bunch, and when a bunch of handsome/beautiful pioneers (physicists) are using a function that isn’t definable, mathematicians can’t help but be helpful.  When they bother, physicists usually define the delta function as the limit of a series of progressively thinner and taller functions (usually Gaussians).

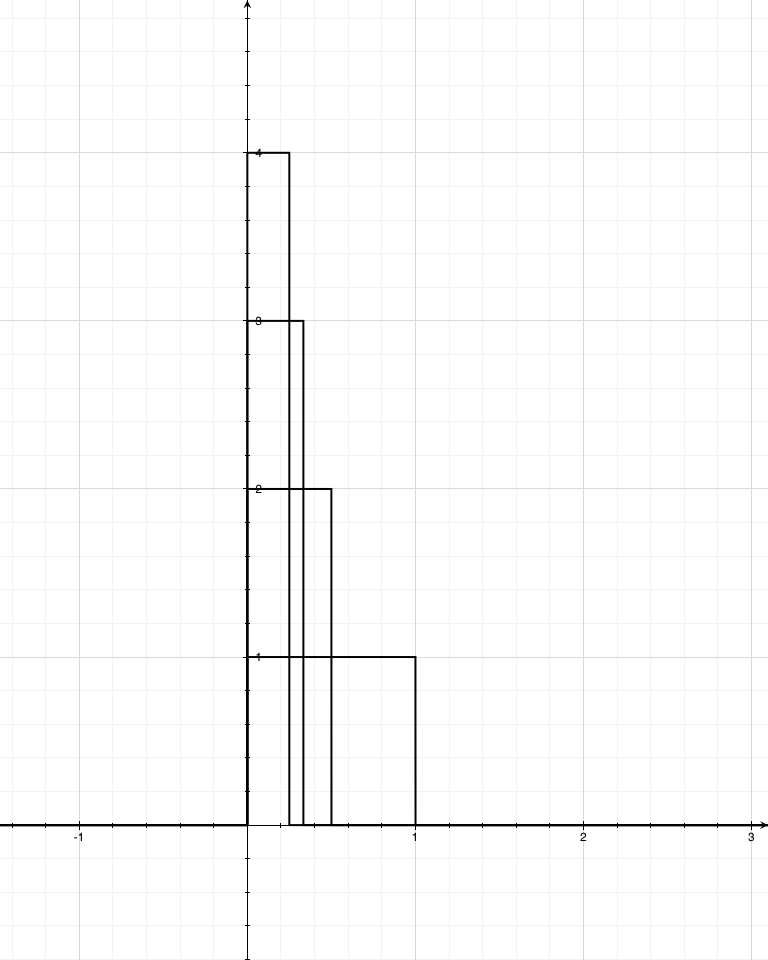
One of the simplest ways to construct the delta function is the series of functions f_n(x) = n, 0 ≤ x ≤ 1/n (the first four of which are shown).  The area under each of these is 1, and most/many of the important properties of delta functions can be derived by looking at the limit as n→∞.

Mathematicians take a different tack.  For those brave cognoscenti, the delta function isn’t a function at all; instead it’s a “distribution”, which is a member of the dual of function space, and it’s used to define a “bounded linear functional”.

So that’s one issue cleared up.

A “functional” takes an entire function as input, and spits out a single number as output.  When you require that the functional is linear (and why not?), you’ll find that the only real option is for the functional to take the form .  This is because of the natural linearity of the integral:

In , F is the functional, f(x) is the distribution corresponding to that functional, and g(x) is the function being acted upon.  The delta function is the distribution corresponding to the functional which simply returns the value at zero.  That is, .  So finally, what in the crap does “returning the value at zero” have to do with the derivative of the Heaviside function?  As it happens: buckets!

Assume here that A<0<B,

Running through the same process again, you’ll find that this is a halfway decent way of going a step further and defining the derivative of the delta function, δ'(x).

δ'(x) also isn’t a function, but is instead another profoundly abstract distribution.  And yes: this can be done ad nauseam (or at least ad queasyam) to create distributions that grab higher and higher derivatives of input functions.