Q: How many times do you need to roll dice before you know they’re loaded?

Physicist: A nearly equivalent question might be “how can you prove freaking anything?”.

In empirical science (science involving tests and whatnot) things are never “proven”.  Instead of asking “is this true?” or “can I prove this?” a scientist will often ask the substantially more awkward question “what is the chance that this could happen accidentally?”.  Where you draw the line between a positive result (“that’s not an accident”) and a negative result (“that could totally happen by chance”) is completely arbitrary.  There are standards for certainty, but they’re arbitrary (although generally reasonable) standards.  The most common way to talk about a test’s certainty is “sigma” (pedantically known as a “standard deviation“), as in “this test shows the result to 3 sigmas”.  You have to do the same test over and over to be able to talk about “sigmas” and “certainties” and whatnot.  The ability to use statistics is a big part of why repeatable experiments are important.

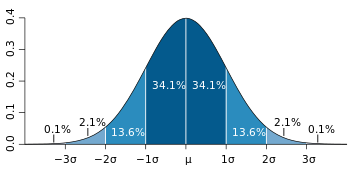
When you repeat experiments you find that their aggregate tends to look like a “bell curve” pretty quick.  This is due to the “central limit theorem” which (while tricky to prove) totally works.

“1 sigma” refers to about 68% certainty, or that there’s about a 32% chance of the given result (or something more unlikely) happening by chance.  2 sigma certainty is ~95% certainty (meaning ~5% chance of the result being accidental) and 3 sigmas, the most standard standard, means ~99.7% certainty (~0.3% probability of the result being random chance).  When you’re using, say, a 2 sigma standard it means that there’s a 1 in 20 chance that the results you’re seeing are a false positive.  That doesn’t sound terrible, but if you’re doing a lot of experiments it becomes a serious issue.

The more data you have, the more precise the experiment will be.  Random noise can look like a signal, but eventually it’ll be revealed to be random.  In medicine (for example) your data points are typically “noisy” or want to be paid or want to be given useful treatments or don’t want to be guinea pigs or whatever, so it’s often difficult to get better than a couple sigma certainty.  In physics we have more data than we know what to do with.  Experiments at CERN have shown that the Higgs boson exists (or more precisely, a particle has been found with the properties previously predicted for the Higgs) with 7 sigma certainty (~99.999999999%).  That’s excessive.  A medical study involving every human on Earth can not have results that clean.

So, here’s an actual answer.  Ignoring the details about dice and replacing them with a “you win / I win” game makes this question much easier (and also speaks to the fairness of the game at the same time).  If you play a game with another person and either of you wins, there’s no way to tell if it was fair.  If you play N games, then (for a fair game) a sigma corresponds to excess wins or losses away from the average.  For example, if you play 100 games, then

1 sigma: ~68% chance of winning between 45 and 55 games (that’s 50±5)

2 sigma: ~95% chance of winning between 40 and 60 games (that’s 50±10)

If you play 100 games with someone, and they win 70 of them, then you can feel fairly certain (4 sigmas) that something untoward is going down because there’s only a 0.0078% chance of being that far from the mean (half that if you’re only concerned with losing).  The more games you play (the more data you gather), the less likely it is that you’ll drift away from the mean.  After 10,000 games, 1 sigma is 50 games; so there’s a 95% chance of winning between 4,900 and 5,100 games (which is a pretty small window).

Keep in mind, before you start cracking kneecaps, that 1 in 20 people will see a 2 sigma result (that is, 1 in every N folk will see something with a probability of about 1 in N).  Sure it’s unlikely, but that’s probably why you’d notice it.  So when doing a test make sure you establish when the test starts and stops ahead of time.