Q: How does “1+2+3+4+5+… = -1/12” make any sense?

Physicist: When wondering across the vast plains of the internet, you may have come across this bizarre fact, that , and immediately wondered: Why isn’t it infinity?  How can it be a fraction?  Wait… it’s negative?

An unfortunate conclusion may be to say “math is a painful, incomprehensible mystery and I’m not smart enough to get it”.  But rest assured, if you think that , then you’re right.  Don’t let anyone tell you different.  The thing falls out of an obscure, if-it-applies-to-you-then-you-already-know-about-it, branch of mathematics called number theory.

Number theorists get very excited about the “Riemann Zeta Function”, ζ(s), which is equal to whenever this summation is equal to a number.  If you plug s=-1 into ζ(s), then it seems like you should get , but in this case the summation isn’t a number (it’s infinity) so it’s not equal to ζ(s).  The entire -1/12 thing comes down to the fact that , however (and this is the crux of the issue), when you plug s=-1 into ζ(s), you aren’t using that sum.  ζ(s) is a function in its own right, which happens to be equal to for s>1, but continues to exist and make sense long after the summation stops working.

The bigger s is, the smaller each term, , and ζ(s) will be.  As a general rule, if s>1, then ζ(s) is an actual number (not infinity).  When s=1, .  It is absolutely reasonable to expect that for s<1, ζ(s) will continue to be infinite.  After all, ζ(1)=∞ and each term in the sum only gets bigger for lower values of s.  But that’s not quite how the Riemann Zeta Function is defined.  ζ(s) is defined as when s>1 and as the “analytic continuation” of that sum otherwise.

You know what this bridge would do if it kept going.  “Analytic continuation” is essentially the same idea; take a function that stops (perhaps unnecessarily) and continue it in exactly the way you’d expect.

The analytic continuation of a function is unique, so nailing down ζ(s) for s>1 is all you need to continue it out into the complex plane.

Complex numbers take the form “A+Bi” (where ).  The only thing about complex numbers you’ll need to know here is that complex numbers are pairs of real numbers (regular numbers), A and B.  Being a pair of numbers means that complex numbers form the “complex plane“, which is broader than the “real number line“.  A is called the “real part”, often written A=Re[A+Bi], and B is the “imaginary part”, B=Im[A+Bi].

That blow up at s=1 seems insurmountable on the real number line, but in the complex plane you can just walk around it to see what’s on the other side.

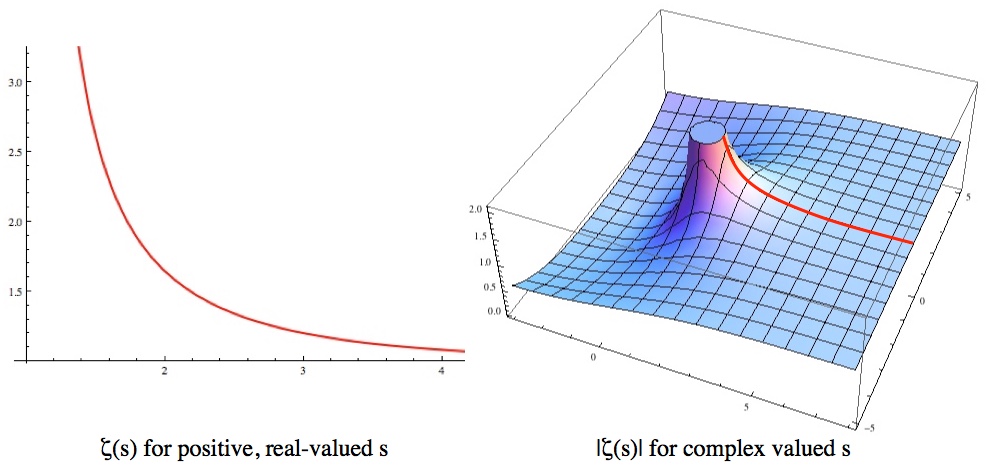
Left: ζ(s) for values of s>1 on the real number line. Right: The same red function surrounded by its “analytic continuation” into the rest of the complex plane.  Notice that, except for s=1, ζ(s) is completely smooth and well behaved.

defines a nice, smooth function for Re[s]>1.  When you extend ζ(s) into the complex plane this summation definition rapidly stops making sense, because the sum “diverges” when s≤1.  But there are two ways to diverge: a sum can either blow up to infinity or just never get around to being a number.  For example, 1-1+1-1+1-1+… doesn’t blow up to infinity, but it also never settles down to a single number (it bounces between one and zero).  ζ(s) blows up at s=1, but remains finite everywhere else.  If you were to walk out into the complex plane you’d find that right up until the line where Re[s]=1, ζ(s) is perfectly well-behaved.  Looking only at the values of ζ(s) you’d see no reason not to keep going, it’s just that the formulation suddenly stops working for Re[s]≤1.

But that’s no problem for a mathematician (see the answer gravy below).  You can follow ζ(s) from the large real numbers (where the summation definition makes sense), around the blow up at s=1, to s=-1 where you find a completely mundane value.  It’s .  No big deal.

So the thing is entirely about math enthusiasts being so (justifiably) excited about ζ(s) that they misapply it, and has nothing to do with what 1+2+3+… actually equals.

This shows up outside of number theory.  In order to model particle interactions correctly, it’s important to take into account every possible way for that interaction to unfold.  This means taking an infinite sum, which often goes well (produces a finite result), but sometimes doesn’t.  It turns out that physical laws really like functions that make sense in the complex plane.  So when “1+2+3+…” started showing up in calculations of certain particle interactions, physicists turned to the Riemann Zeta function and found that using -1/12 actually turned out to be the right thing to do (in physics “the right thing to do” means “the thing that generates results that precisely agree with experiment”).

A less technical shortcut (or at least a shortcut with the technicalities swept under the rug) for why the summation is -1/12 instead of something else can be found here.  For exactly why ζ(-1)=-1/12, see below.

Answer Gravy: Figuring out that ζ(-1)=-1/12 takes a bit of work.  You have to find an analytic continuation that covers s=-1, and then actually evaluate it.  Somewhat surprisingly, this is something you can do by hand.

Often, analytically continuing a function comes down to re-writing it in such a way that its “poles” (the locations where it blows up) don’t screw things up more than they absolutely have to.  For example, the function only makes sense for -1<z<1, because it blows up at z=1 and doesn’t converge at z=-1.

f(z) can be explicitly written without a summation, unlike ζ(s), which gives us some insight into why it stops making sense for |z|≥1.  It just so happens that for |z|<1, .  This clearly blows up at z=1, but is otherwise perfectly well behaved; the issues at z=-1 and beyond just vanish.  f(z) and  are the same in every way inside of -1<z<1.  The only difference is that doesn’t abruptly stop, but instead continues to make sense over a bigger domain.  is the analytic continuation of  to the region outside of -1<z<1.

Finding an analytic continuation for ζ(s) is a lot trickier, because there’s no cute way to write it without using an infinite summation (or product), but the basic idea is the same.  We’re going to do this in two steps: first turning ζ(s) into an alternating sum that converges for s>0 (except s=1), then turning that into a form that converges everywhere (except s=1).

For seemingly no reason, multiply ζ(s) by (1-2^1-s):

So we’ve got a new version of the Zeta function, , that is an analytic continuation because this new sum converges in the same region the original form did (s>1), plus a little more (0<s≤1).  Notice that while the summation no longer blows up at s=1, does.  Analytic continuation won’t get rid of poles, but it can express them differently.

There’s a clever old trick for shoehorning a summation into converging: Euler summation.  Euler (who realizes everything) realized that for any y.  This is not obvious.  Being equal to one means that you can pop this into the middle of anything.  If that thing happens to be another sum, it can be used to make that sum “more convergent” for some values of y.  Take any sum, , insert Euler’s sum, and swap the order of summation:

If the original sum converges, then this will converge to the same thing, but it may also converge even when the original sum doesn’t.  That’s exactly what you’re looking for when you want to create an analytic continuation; it agrees with the original function, but continues to work over a wider domain.

This looks like a total mess, but it’s stunningly useful.  If we use Euler summation with y=1, we create a summation that analytically continues the Zeta function to the entire complex plane: a “globally convergent form”.  Rather than a definition that only works sometimes (but is easy to understand), we get a definition that works everywhere (but looks like a horror show).

This is one of those great examples of the field of mathematics being too big for every discovery to be noticed.  This formulation of ζ(s) was discovered in the 1930s, forgotten for 60 years, and then found in an old book.

For most values of s, this globally convergent form isn’t particularly useful for us “calculate it by hand” folk, because it still has an infinite sum (and adding an infinite number of terms takes a while).  Very fortunately, there’s another cute trick we can use here.  When n>d, .  This means that for negative integer values of s, that infinite sum suddenly becomes finite because all but a handful of terms are zero.

So finally, we plug s=-1 into ζ(s)

Keen-eyed readers will note that this looks nothing like 1+2+3+… and indeed, it’s not.

(Update: 11/24/17)

A commenter pointed out that it’s a pain to find a proof for why Euler’s sum works.  Basically, this comes down to showing that .  There are a couple ways to do that, but summation by parts is a good place to start:

You can prove this by counting how often each term, , shows up on each side.  Knowing about geometric series and that is all we need to unravel this sum.

That “…” step means “repeat n times”.  It’s worth mentioning that this only works for |1+y|>1 (otherwise the infinite sums diverge).  Euler summations change how a summation is written, and can accelerate convergence (which is really useful), but if the original sum converges, then the new sum will converge to the same thing.