Q: With entangled particles, can you tell when/how the other particle is measured?

Physicist: Nope!  You definitely can’t.

Almost without exception, when you hear about quantum entanglement it’s described as some kind of communication or connection.  Generally along the lines of “when you affect one entangled particle it instantly affects the other” or slightly more sophisticated “when you measure the state of one entangled particle, the other collapses to the same state”.  But these statements cause more difficulties than a dark room full of loose rope.  They’ve given rise to an endless parade of universally unsuccessful theories about using entanglement to communicate instantaneously between distant locations.  But instantaneous communication has issues.  In particular “instantaneous” is faster than c (the speed of light), which is the fastest speed.  Ultimately, while entangled quantum systems do have plenty of seriously weird properties, being connected to each other is not one of them.

For the most part, entangled particles are like a pair of carefully boxed mail-order coins with the same (random) side up.  If you and a friend shared a pair of these “coin boxes”, you’d find it difficult to tell whether or not your friend had seen their coin without asking.

In very short: if you do the same measurement on each of a pair of entangled particles, the two measurements will produce the same, random result.  But that doesn’t involve any kind of signal bouncing around the universe.  The distant entangled particle is like a lost wallet: there’s no way to tell if someone’s seen it until they call you.

Quick aside: Entanglement takes many forms, not just “always the same” (e.g., “always opposite” is an option).  If you can think of a property of a particle or other quantum system, then you’re thinking of something that can be entangled: particle spin (up vs. down), photon polarization (vertical vs. horizontal), particle position (left path vs. right path), energy levels (excited vs. ground), even existence (is vs. isn’t).  Entanglement is fun stuff.

Quantum systems can be in multiple states at the same time.  For example, an electron can be both spin up and spin down.  The question “which is it: up or down?” genuinely doesn’t make sense, because the electron’s state can be a combination of both.  We call such combinations “superpositions”.  Quantum superpositions are famously delicate.  You can demonstrate that an electron is in multiple states, but you have to be clever about it, because if you ever directly measure whether the electron is spin up or down, you always find that it’s one or the other, but never both.  Which single state you find is fundamentally random.  This “effect” of measurement, where a superposition of several states is suddenly replaced by only one of those states, is called “decoherence” or “wave function collapse” or (when you’re in a hurry) “collapse”.

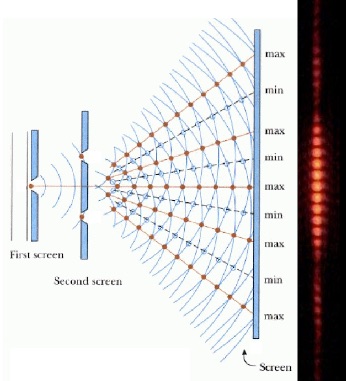
The oldest method to infer the superposition of states is the double slit experiment.  Particles of any kind demonstrate that they can go through both slits (are so are in a superposition of both top path and bottom path) since the two paths/states interfere to create a pattern.  But if you ever directly check, you only see particles going through one slit or the other.  There are similar experiments for spin.

If a pair of electrons share a common state (for example by both being up and both being down, but never one up / one down), then those electrons are “entangled”.  A pair of entangled particles are in a superposition of states together.

Entanglement isn’t something that happens accidentally.  Or rather, it happens all the time (almost every interaction on every level generates entanglements), but useful entanglement is really hard to set up.  It’s like the fact that practically everything makes sound, but the dulcet tones of a barbershop quartet takes work (and three friends).  In order for two things to be entangled they need to have interacted with each other, so you can’t just cause two distant particles to become entangled.  Generally speaking, you entangle two particles when they’re together, then move them apart.

When a single particle in a superposition of states is measured, it collapses to one of the states in its superposition.  Entangled particles have the same rule; when you measure either of them you find that they’re in only one state.  But since they’re in a shared state, a measurement on the other will yield the same result.  A direct measurement is made, so the superposition (both up and both down) collapses and only a single state is left (either both up or both down).  The fact that there are two particles involved instead of one doesn’t change things.

Einstein infamously quipped that entanglement is “spooky action at a distance” because, despite the fact that the result of each collapse is absolutely random, when it happens to a pair of entangled particles, they still manage to agree.  That would seem to imply that they’re somehow telling each other how to behave (even if they would need to do so across any barrier or even faster than light).

Tricks that use entanglement to instantly send information generally involve collapsing the state of the distant particle (by measuring your own), and assuming that the person in charge of that particle will somehow notice.  Unfortunately (and this is the answer), there’s no “new-particle-smell” for particles that are still in superpositions and there’s no big flash when that superposition collapses.  If you measure an electron’s spin the result is simply “spin up” or “spin down”.  That’s all you get.  But that doesn’t tell you what the state was before, or if the original state was a superposition of several states, or even if the particle was entangled with something else.

If you only have access to one particle, then the two situations, 1) the other particle is inaccessible or 2) it has been quietly measured, are indistinguishable in every physical sense.  Regardless of whatever else is involved, you can never notice the weirdness of entangled pairs until you directly compare them with each other.

The fact that you can’t tell the difference between a random state and an entangled state is super not obvious.  In fact, the Fundamental Fysiks Group (who aren’t physicists so much as parapsychologists) once came up with a clever method for using entanglement for faster-than-light communication, that wasn’t clearly non-sense.  Normally the way we determine that something is in multiple states is to prepare many identical versions and test them out, so the Fundamental Fysikists proposed copying one of the entangled particles and doing tests on the ensemble.  In theory, Alice could communicate one bit of information by either looking (collapse) or not looking (no collapse) at her particle, and if Bob copied his particle many times and compared their behavior, he would be able to tell the difference.  Technically, Bob might be able to tell the difference before Alice bothered to look, which is… suspicious (such is the nature of instantaneous communication in a universe where special relativity holds sway).

Faced with such daunting bizarritudes and paradoxes, professional physicists decided to take notice and “fix” the issue by carefully examining all of the assumptions that went into this cute trick (evidently, doing physics carefully is what separates physicists from fysiksists).  It turns out that copying a quantum state is impossible and if it weren’t for the Fundamental Fysiks Group, we wouldn’t have had figured it out quite as soon as we did.  The result of that figuring is the “no-cloning” or “better luck next time Fysikists” theorem.

Answer Gravy: A cute way to prove to yourself that superposition can’t be measured is to notice that “superposition-ness” is subjective.  That is to say, a given quantum state can be a single state from one perspective and a superposition of several states from another.  This is easiest to picture with polarized light.

A “measurement basis” is the set of states that your measurement apparatus can distinguish.  For example, if you’re using a vertical polarizing filter, then you can distinguish between light that is vertically polarized ( passes through) and horizontally polarized ( is stopped).  So for a vertical (or horizontal) filter the measurement basis is .

But light can be polarized at any angle (there’s nothing special about verticalness).  So what happens when diagonally polarized light hits a vertical filter?  It turns out that diagonally polarized light, , is a superposition of both and .  When you measure diagonal light in the basis, those are the only two possible results.  So when you actually do this, you find that the diagonal photon is suddenly either vertical or horizontal.  The superposition of vertical and horizontal states in the diagonal photon collapses to only one of those states.  Which state will remain is fundamentally random.

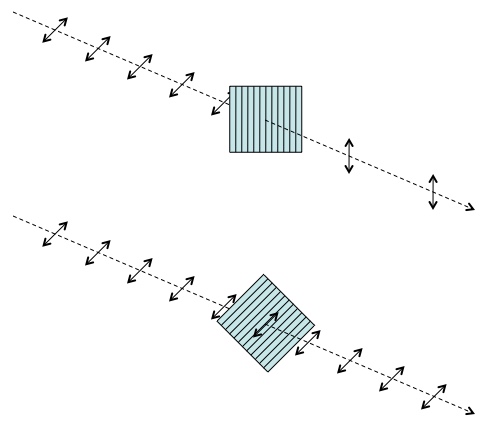
Top: When diagonally polarized light hits a vertical filter, its state randomly collapses to either vertical (it passes through) or horizontal (it stops).  This is because diagonally polarized light is a superposition of both vertical and horizontal states.  Bottom: On the other hand, it always passes through a similarly diagonal filter.  For such a filter, the photons are in a single state.  No collapse.

However!  A diagonal filter measures photon polarization in the basis.  If the incoming state is one of those diagonal states, then the diagonal filter will determine which.  When you measure diagonal photons with a similarly diagonal filter, they always pass through and there’s no collapse to either of the vertical/horizontal states.

Brace yourself for the point.  The same state, , is a single state when measured in the basis and a superposition of states when measured in the basis.  There’s a lot to unpack there, but the take-home is this: a state is a state is a state.  There is no way to tell whether a thing is in a superposition or has collapsed, because there is fundamentally nothing different about the two situations.  No matter what the state of a thing is, it is always possible to find a measurement basis where the state is a superposition and another basis where it’s a single state.

Slightly Deeper Gravy: Entangled particles are nothing special.  An entangled state is a regular, dull as dishwater, quantum state, it’s just that it’s shared between multiple particles.  There actually is a “correct” basis in which you always get definite results from entangled particles, but you need all of the involved particles in one place to do such a measurement.  Without all the pieces, you always get random results.

A diagonal state owned by Alice looks like this: .  The subscript “a” means “owned by Alice”.  This notation says that if Alice measures her photon in the basis, there is a chance of either result according to the Born rule.  The other diagonal state is .  Both of these diagonal states produce random results in the basis, but produce definite results in the basis.

Notice that the converse is also true.  and , so the vertical and horizontal states are superpositions of the diagonal states and therefore produce random results in the diagonal basis.  For each of these states (or any other for that matter), there is a measurement basis where they give definite results.

But for entangled states, if you only have access to one of the two particles, there is no “correct basis” where you always get a definite result.

A nice, tidy entangled state distributed between Alice and Bob is .  This notation says that if either Alice or Bob do a measurement in the basis they’ll get a random result.  So what about the diagonal basis?  Just rewrite the state:

Holy crap!  It’s essentially the same state in the diagonal basis!  Once again, it’s perfectly random (50% chance of either result).  More generally, as long as you only have one particle, the results are just as random in any basis.  It turns out this is one of those universal truths of entangled states: it doesn’t matter how you measure them, if you’re only looking at one particle, you’re using the “wrong” basis.

On the other hand, if you have both particles, you can tell the difference between the four “maximally entangled states“.  Each particle’s state is described by a qubit (a “quantum bit”).  First, perform a controlled not gate (CNot) on the two entangled qubits, then apply a Hadamard gate (H) on the control qubit, then measure both.

Controlled Not does this:

Hadamard does this:

In the case of photon polarization, the Hadamard gate is a rotation that switches between the vertical/horizontal basis and the diagonal basis.

Here’s what happens to the entangled state this post keeps talking about:

There are four maximally entangled states for pairs of two-state systems.  Doing the same operations to each yields:

These are different, definite states!  So this is how to look at entangled two-state systems in the “correct” basis.  But it wouldn’t be possible to do this without the CNot operation and that requires both particles to work.

The coin box pictures are from here.