Q: Why does gravity pull things toward the center of mass? What’s so special about the center of mass?

The original question was: How do you measure d in the equation for universal gravitation ()?  It can’t be the distance between the surfaces of the objects, or when they touched f would be “infinite.”  It can’t be the distance between their centers of masses because if I shot a bullet into a rubber ball their centers of mass might coincide, and again d would be zero.  It can’t be the distance between the center of mass of one object and the surface of the other object, because there would be two possible d’s.

Physicist: Nature abhors a singularity.  So when you see a nice glaring one (like this case, where d=0 makes the force jump to infinity) it’s worth pausing to consider how the universe finagles its way out.  When you apply Newton’s Law of Universal Gravitation, , to planets and stars, d is indeed the distance between the centers of mass.  But when to use that standard and why it works is a little subtle.

One of the most important ideas in physics is that the exact same laws apply to everything, everywhere, always.  Nothing and nowhere gets special treatment, and that includes the center of mass.

Nothing is sacred.

The stuff at the center of the Earth does pull on you, but that’s nothing special; so does literally everything else.  Phone books, your worst enemy, that thing you saw that one time, everything on Earth (and otherwise) pulls on you according to Newton’s law.  Every atom pulls on every other atom.

All mass creates gravity and pulls things toward it.  Here on Earth, we always feel a pull toward the center of the Earth (top), so it might seem as though there’s something special down there.  In reality, we’re experiencing the collective pull of everything in and on the Earth (bottom).

The reason you don’t notice a pull toward each individual thing around you is that gravity is weak.  The physical (as opposed to emotional) attraction between you and someone you’re walking next to is a force on the order of the weight of a mote of dust (tens of nanograms).  The air moving in and out of your lungs pushes you around far, far more.

The reason you do notice a pull toward the Earth is that there’s a lot of Earth to do the pulling; around 100,000,000,000,000,000,000,000 times the mass of the person next to you.  Sure it’s farther away (around 4,000 miles on average), but there’s a lot of it.  Heck, it blocks half the sky (the lower half).

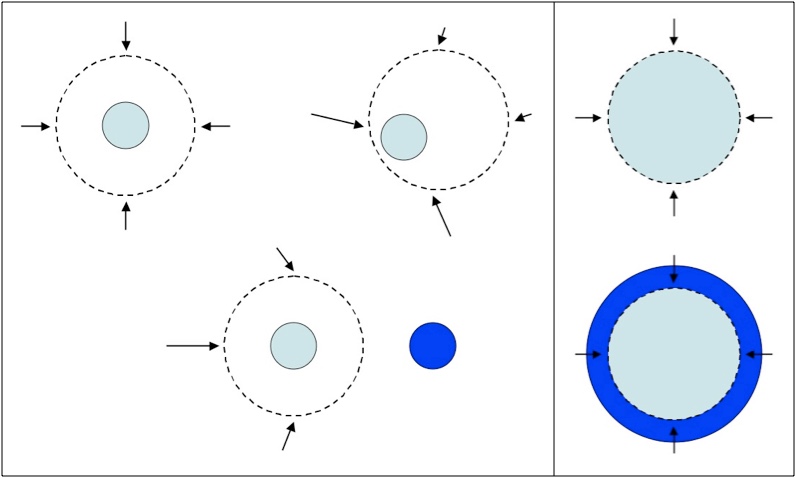
Finally, the reason everyone feels a pull toward the center of the Earth is that, for most intents and purposes, the Earth is a perfect sphere.  No matter where you are and no matter how you look at it, you can draw a line through the middle of the Earth and the two sides will be mirror opposites of each other.  As much as one half pulls you to the right, the other pulls you to the left.  The collective pull of both halves is right down the middle; toward the line between them.

The matter on the left side of the (red) line pulls you down and to the left, the matter on the right pulls you down and to the right.  Because the two sides are essentially the same, the “left-and-right-ness” cancel out, leaving a net down.  For a sphere, you can repeat the same argument for any (yellow) line through the center.

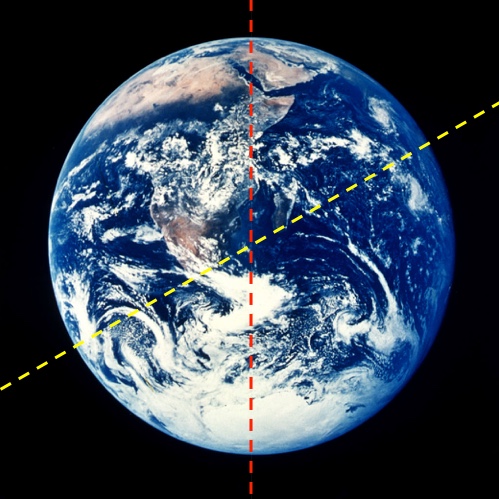
The same argument applies to any line that separates the two halves, and all of those lines pass through the center of mass.  Technically, that’s how the center of mass is defined.  So, because the mass of the Earth is spherically symmetric, gravity around here points toward the center of mass.

However!  Gravity does not, in general, point toward the center of mass.  Take for example the Earth-Moon system.  Despite its non-contiguous-ness, it’s still a perfectly legit collection of mass.  The center of mass of the Earth and Moon combined is a point just a little below the Earth’s surface.  That fact is important when you consider how the two orbit each other (the Moon circles that point while the Earth kinda wobbles around it), but it is almost entirely unimportant when you consider how gravity pulls on things presently sitting on Earth’s surface.

The Earth-Moon system to scale.  Notice that gravity does not pull you toward this system’s center of mass (the red dot) it pulls you toward the largest nearby thing (the pale blue dot).

That all said, Earth is only almost perfectly spherical.  You may have noticed that the world is not a perfectly polished ball; there are mountains, oceans, gigatons of missing single socks, and that non-uniformity penetrates well below the surface.  Those variations in the distribution and density of mass means that Earth’s gravity changes (very, very slightly) from place to place, both in magnitude and direction.

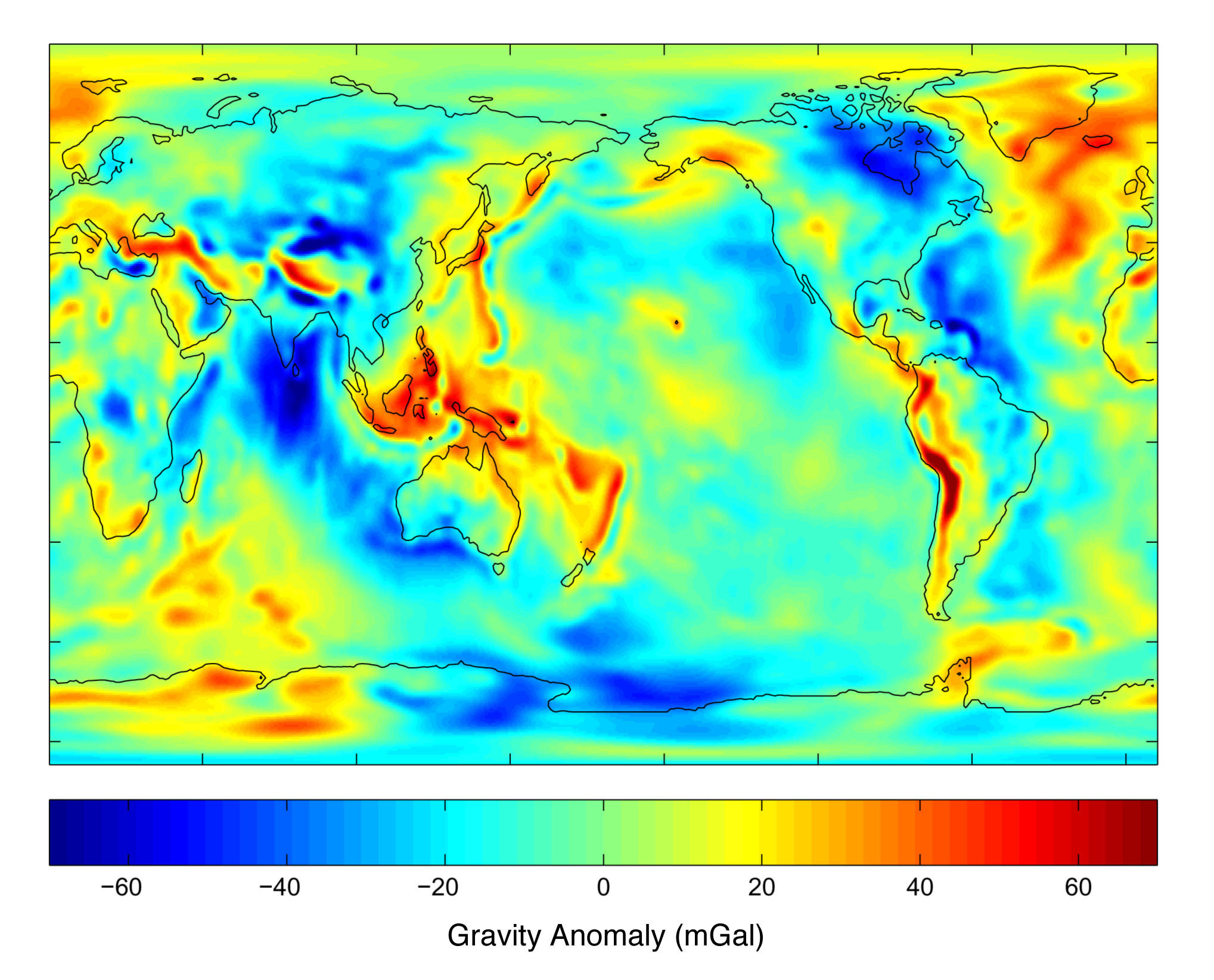
Deviations in the strength of Earth’s gravity.  The average surface gravity of Earth is around 980 Gal (1 Gal = 1 cm/s²).  Surface gravity points away from Earth’s center the farthest where the colors are changing the fastest.

By flying a pair of satellites in formation over the Earth and measuring the distance between them we can detect them speeding up and slowing down with respect to each other as one, then the other, passes over differently-gravity’d regions.

The GRACE (Gravity Recovery And Climate Experiment) satellites, cleverly called “GRACE-1” and “GRACE-2”, shot lasers at each other from 2002 to 2017 to measure Earth’s gravity field over that time.  They were so stupefyingly sensitive that they could detect changes in the location of water and ice through the gravity they generate (hence the “climate” part).

Finally, to more directly address the original question, since gravity is a collective pull toward each individual piece of mass and not necessarily a pull toward the center of mass, Newton’s universal law of gravitation has to be applied with a little finesse.  works fine (with d the distance to the center) as long as you’re outside of a sphere of mass, it stops working as soon as you’re inside because the mass above you counteracts the pull of the mass below you.  In the case of a bullet shot through a rubber ball, this is why the gravitational force never jumps to infinity; the equation that says it should ceases to apply.  The universe always has an obnoxious way to get out of having to deal with singularities.

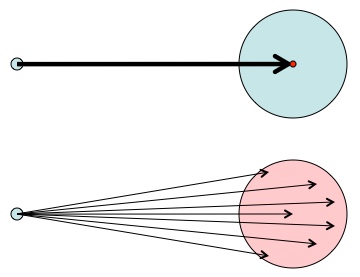
Because gravity is an “inverse square force” (the “” in “” ) it has the remarkable property that the total gravitational field pointing into any closed “bubble” is proportional to the amount of mass contained within that bubble.  Inverse square laws also describe the way light gets dimmer with distance: so if you build a glass bubble around a light source, no matter how big or what shape the bubble is, the same total amount of light flows out of it.

Left: The force through any particular part of the bubble can change, but the total depends only on the amount of mass inside.  Right: If the mass is distributed spherically, then the force is the same everywhere on a spherical bubble (what would make it different?) and we can see why the outer layers of a planet have no impact on the gravity inside of a planet.

The beauty of this is that it allows us to do what should be an arduous calculation (adding up the contribution from every tiny chunk of matter) in a manner that appeals to physicists: stupid easy and deceptively impressive.  One of the immediate conclusions of this is that, as long as you’re outside of the sphere of mass in question, there’s no difference between the gravity of a sphere of mass and the same amount of mass concentrated at a point.  So if the Sun collapsed into a black hole, everything in the solar system would continue to orbit it as though nothing had happened, because the gravity would only have changed below where the surface of the Sun used to be.

The second cute conclusion of this is that if you’re inside of a sphere of mass, only the layers below you count toward the gravity you feel.  So the closer you are to the center, the less mass is below you, and the less gravity there is.  If you were in an elevator that passed through the Earth, you’d know you were near the center because there’d be no gravity.  With the same amount of mass in every direction, every atom in your body would be pulled in every direction equally, and so not at all.  A sort of gravitational tug of war stalemate.

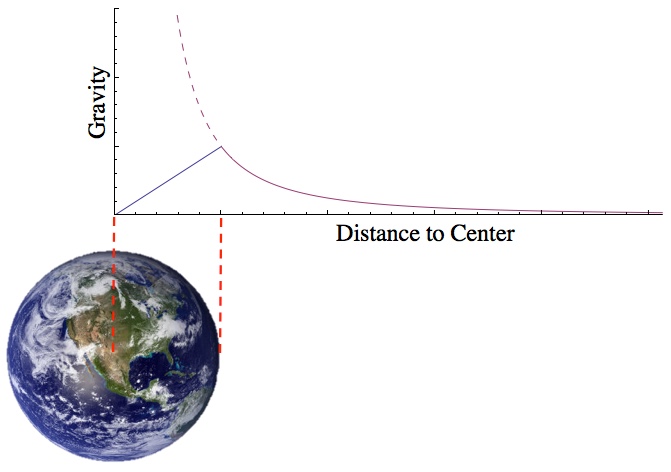
As you approach a sphere of mass gravity increases by the inverse square law, but drops linearly inside the sphere.  If the density varies (which it usually does), that straight line will bow up a bit.

Newton’s Universal Law of Gravitation applies to everything (hence the “universal”).  But instead of applying to the centers of mass of pairs of big objects, it applies to every possible pair of pieces of matter.  In the all-to-common-in-space case of spheres, we can pretend that entire planets and stars are points of mass and apply Newton’s laws to those points, but only as long as we don’t need perfection (which is usually).  As soon as things start knocking into each other, or the subtle effects of their not-sphere-ness become important, you’re back to carefully tallying up the contribution from every chunk of mass.

The pedestal with nothing on it used to have a guy stabbing a bird.  The picture is from here.

The GRACE stuff is from NASA.