Q: Is π the same in every universe?

Mathematician: That depends on what you mean by “universe.”  Here’s a framing:

A circle of radius R centered at a point P is the set of all points in the plane with distance R from P.  The diameter D of this circle is twice the radius, but can also be thought of as the longest possible straight-line path from a point on the circle to another point on the circle.  The circumference C of the circle is its arc length.  By definition, Pi = C/D.

We usually think about distance as “how the crow flies” and the shortest path between two points is a straight line, but think about how you might get around in a well-gridded city.  You either walk north to south or east to west.  You can turn at corners, but each moment spent walking is either purely vertical or horizontal.  If a mathematician gridded a city, we might think about (0,0) as the city center (the intersection of 0th Ave and 0th St).  What points are exactly 5 blocks away?  Clearly (0,5), (5,0), (0,-5), and (-5,0) (yes, negative streets and avenues!) have shortest distance paths of length 5.  But so do (2,3) and (-1,4).  You can convince yourself that to get to the point (a,b), you’re going to have to travel at least |a| in horizontally and |b| vertically, so the distance from (0,0) to (a,b) is at least |a|+|b| blocks, and it’s easy to see a path that gets you there in exactly |a|+|b|.  There might be many paths from (0,0) to (2,3) (consider ENENN or NENEN or NNNEE, for a few northeastern routes there), but all of the shortest ones take 5 blocks, like these.

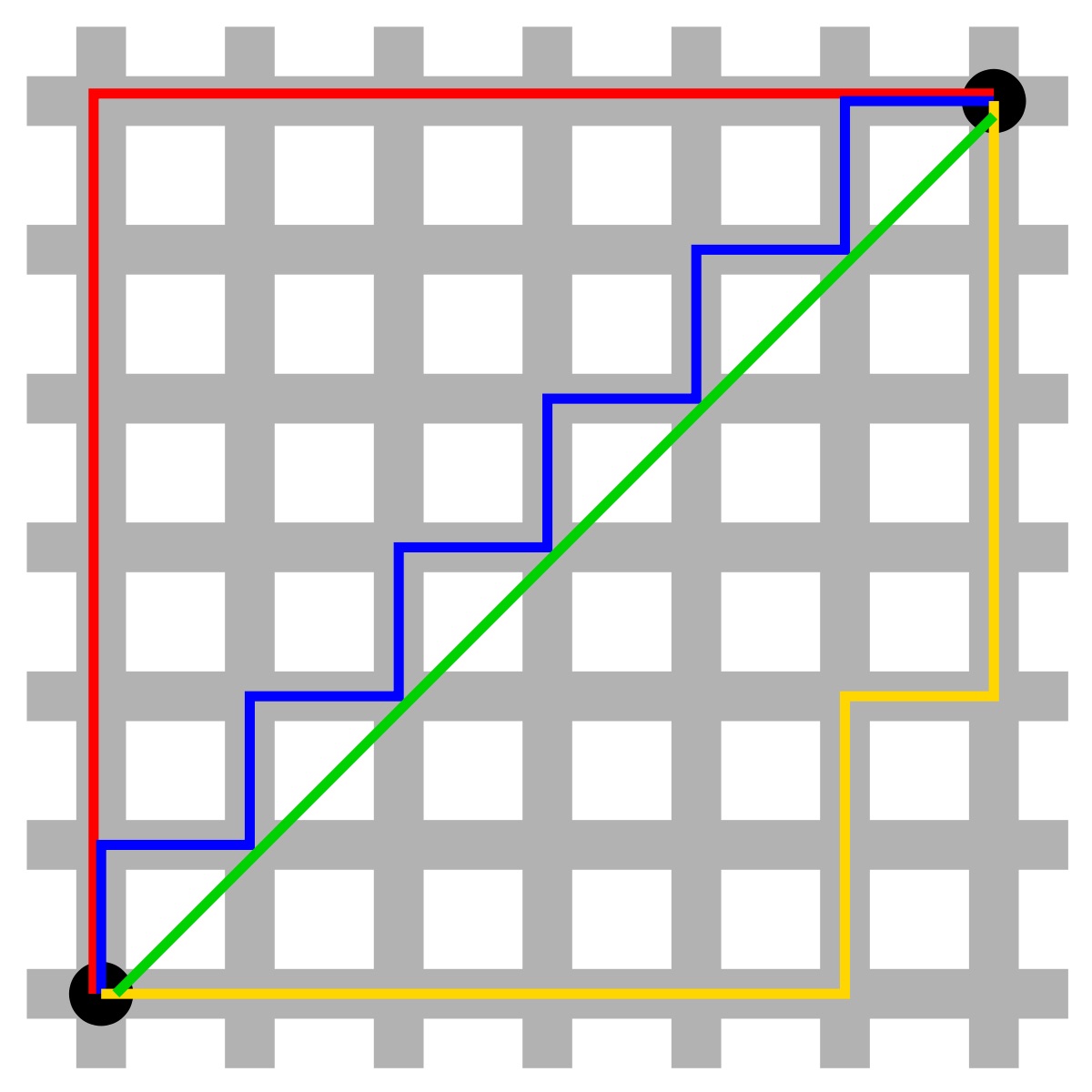
Two points separated by a taxi cab distance of 12.  The red, blue, and yellow routes all cover 12 blocks.  The green line is the “how the crow flies” distance.

If we accept this “taxi cab” sense of distance, we can consider all of the points that have distance R from (0,0) and we would find it looks more like a diamond, since they satisfy |x|+|y| = R instead of sqrt(x^2 + y^2) = R.  The boundary is actually given by four lines: 

x+y = R

x-y = R

-x+y = R

-x-y = R

which gives the outline of a square at a 45-degree tilt.  Each of the side segments has length (in the usual sense of length!) of R*sqrt(2), but we might want to stick to our taxi cab sense of distance and instead of concluding the perimeter has length 8*R instead of 4*R*sqrt(2), the logic being the distance from (0,R) to (R,0) is 2R and we have to make 4 such trips to wind around the perimeter.  If we take two points on the perimeter (a,b) and (c,d), the distance between them will be |a-c| + |b-d|, which you can convince yourself will always be less than or equal to 2R (regardless whether your sense of length is the usual or the taxi length!) and equals 2R from one far corner to another, so we might feel comfortable calling the “diameter” of this “circle” 2R.  In this case, our taxi cab Pi would be Pi = C/D = (8R)/(2R) = 4.

Different notions of distance produce different notions of Pi.  If you know some calculus, you might get a kick out of this paper, which explores Pi as this ratio with respect to a bunch of different related distance systems, including both our usual system, this taxi system, and a spectrum that both lie on:

https://www.jstor.org/stable/2687579

If you’re committed to the usual notion of distance, then we’re stuck with the 3.14159265… business.

Physicist: There are a lot of physical constants in the universe; the strength of gravity, the strength of electric fields, the speed of light, the rate of the universe’s expansion, and on and on.  The vast, vast, vast majority of the possible combinations of values of these physical constants produce boring universes, like a single huge black hole or just diffuse clouds of hydrogen without stars.  There doesn’t seem to be a good reason for the constants to be what there are, save one: there are critters (people) running around saying things like “What’s going on?  The universe is so inexplicably balanced that I can exist and say things like ‘What’s going on?’.”

The philosophy here is a little pessimistic.  Existence isn’t kind, it just accidentally has pockets where it’s not actively mean.  For example, given the absolutely over-the-top number of planets in the universe, it’s not too surprising that at least one of them isn’t completely inhospitable and not surprising at all that we happen to live there.  The argument for there being lots of universes with different physical constants is similar.  Nobody likes either scenario a lot.  If there’s one universe that happens to be nigh-perfect then we need a lot of luck, and if we don’t want to invoke luck, then we need lots of universes.  All that to say, it’s not completely unreasonable to suppose that there are lots of universes and that π might take different values.

However, there’s a big difference between physical constants and mathematical constants.  For example, the gravitational constant (a physical constant) is , where is the uncertainty in the value of G.  That uncertainty is due to the fact that we have to measure G and no measurement is perfect.  We can’t derive its value, so we have to “ask the universe” using experiments.  π on the other hand is a mathematical constant, which can be derived.  It’s a “Platonic Ideal”, like a point, straight line, perfect circle, or any other mathematical idea.  We can imagine these things, but there are no examples of them in reality.  Mathematics is not the study of the universe, it’s the study of logic.  Math “works” because there are plenty of things that are “perfect enough” and plenty of methods for dealing with things that are “not perfect enough”.  We know that π=3.1415926535897932384626433832795028841971693993… not because some enterprising individual went out and measured it, but because a bunch of logicians told a bunch of computers how to figure it out (with the current record for most digits held by this enterprising individual).  Long story short: the value of π has nothing to do with physical reality.

The strict “circumference over diameter” definition of π can have different values depending on the nature of the space involved.  For example, in a curved space (or when restricted to a curved surface) we can measure the circumference and diameter of a circle and find that π is smaller than it should be, because the diameter has a longer trip and is longer than it “should” be.

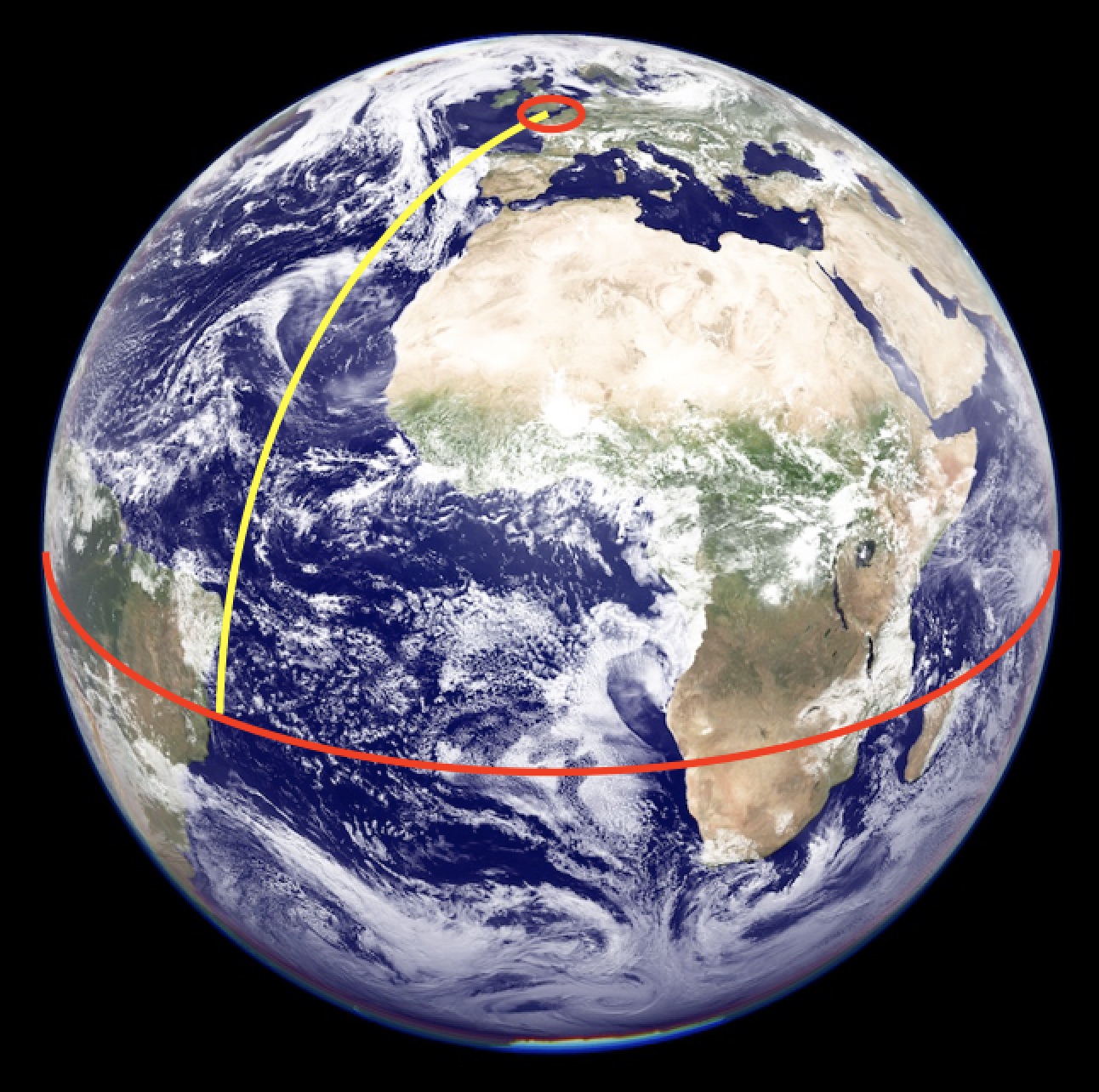
π is the ratio of the circumference (red) to diameter, which is twice the radius (yellow).  If you’re stuck on a sphere using a small circle you find that π=3.1415… and if you use the largest possible circle you find that π=2.

All the same, the denizens of a curved spacetime don’t need to be too dumb to figure this out.  After all, space near Earth is slightly curved (that’s why we have gravity) and that hasn’t interfered with us imagining it flat (dumbness notwithstanding).  If they can imagine Platonic ideals, then with a little work they can figure out how to calculate π just like we have.  All that those other-worldly denizens would need is some notion of smooth space, since small circles in smooth space produce the usual value of π (this is basically the definition of smooth space).

So, do other universes have space like we do?  Unfortunately, we’ve got no experience with other universes and no solid evidence that they exist at all.  What we have are scientific speculations (which is what you get when a scientist guesses).  There’s no standard definition for “parallel universe”, but here are two lists of ideas.  In a nutshell there’s: 1) same universe, but far away, 2) quantum multiverses, 3) related universes with different constants, and 4) “other”.

When things are far enough away, there’s no way to affect anything over there and vice versa, so those places may as well be other universes.  But they’re not really.  Same π.

In the Many World’s interpretation of quantum mechanics the universe we live in seems to split into separate universes.  You’re in a not-special one of them and evidently they’ve got normal space.  Same π.

String theory and eternal inflation imply that new universes are constantly being formed with slightly different physical constants.  Lee Smolin’s “Fecund Universe” theory, where every new universe is a black hole from a higher universe, implies that universes literally evolve to be better at producing black holes.  I like the second idea better than the first, not because either is terribly convincing, but because it’s a cooler.  It scratches a brain itch.  That said, in both of these ideas the new universes are “built on the same scaffold” of spacetime with different numbers of dimensions perhaps, but with the usual notion of space and distance and therefore: same π.

Finally, physicists will sometimes include a catch-all to acknowledge that not everything is known and because as much as we learn, there are always (or at least often) surprises.  That’s the “other” and it’s not really worth worrying about, because… what are we supposed to worry about?  There may be universes out there with completely different notions of distance, but we wouldn’t even recognize them.  In that “maybe… somewhere… somehow…” sense, π can definitely be different.