Physicist: Nopers!
The Heisenberg uncertainty principle, while normally presented in physics circles, is actually a mathematical absolute. So overcoming the uncertainty principle is exactly as hard as overcoming that whole “1+1=2” thing.
The uncertainty principle (the “position/momentum uncertainty principle”) is generally presented like this: you have some particle floating along and you’d like to know its position and its momentum (velocity, whatever) so you bounce a photon off of it (“Bounce a photon off of it” is just another way of saying “try to see it”). A general rule of thumb for light (waves in general really) is high frequency waves propagate in straight lines, and low frequency waves spread out. That’s why sunlight (high frequency) seems to go in a perfectly straight line, but radio waves can spread out around corners. For example, you can still pick up a radio station even when you can’t see it directly.
So, if you want to see where something is with precision you’ll need to use a high frequency photon. After all, how can you trust the results from a wandering, low frequency photon? But, if you use a precise, high-frequency, and thus, high-energy photon, you’ll end up smacking the hell out of the particle you’re trying to measure. So you’ll know where it is pretty exactly, but it’ll go flying off with some unknown amount of momentum. Any method you can come up with to measure the momentum will require you to use low-frequency, low-energy, gentle photons. But then you won’t be able to figure out the particle’s position very well.
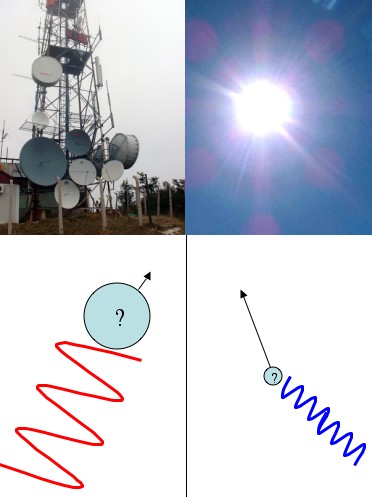
Low frequency photons (like radio waves) don't tell you much about where a particle is, but they doesn't knock it around much either (so you can measure its momentum better). High frequency photons (like sunlight) are terrible at measuring momentum, but can tell you position well.
So far this seems more like an engineering problem than a problem with the universe. Maybe we could arrange things so that the high frequency photon hit softer or something? There was a lot of back and forth for a long time (still is in some circles) about overcoming the uncertainty principle, but in the end it can never be violated.
Rather than being something that’s merely very challenging like, “you can’t break the sound barrier”, “what goes up must come down”, and “you can’t be the world’s best kick-boxer and be the world’s most handsome physicist”, the uncertainty principle is a mathematical absolute. So, unless the basic assumptions of physics are completely wrong (and they’ve held up to some serious scrutiny), the uncertainty principle is in the company of things like “you can’t go faster than light”, “energy and mass are conserved”, and “modern mathematicians don’t have beards” (has anyone else noticed this?). What follows is answer gravy.
Answer gravy: This gravy has some lumps. If you know what a “Fourier transform” is, and are at least a little comfortable with them, then this could be interesting to you.
The square of a quantum wave function is the probability of finding it in a particular state. For example, the “position wave function” can tell you the probability of finding a particle at any position. To get the probability from the wave function, all you have to do is square the wave function.
If you’ve got the quantum wave function for the position of a particle, then you can find the the momentum wave function,
, by taking the Fourier transform of f. That is,
. Now, you can define the uncertainty as the standard deviation of the probability function, which is a really good way to go about it.
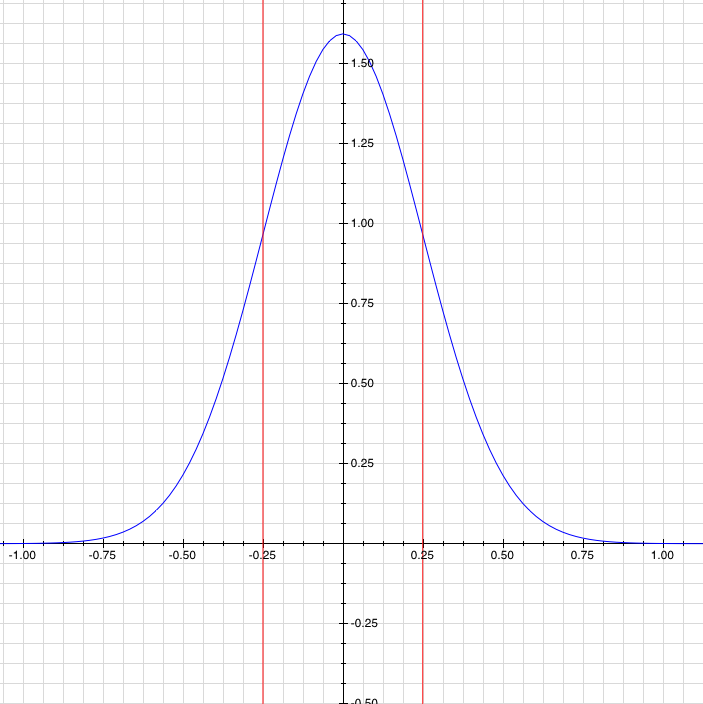
A probability function (blue), with its uncertainty or standard deviation (red). Like you'd expect, the particle is most likely to be near zero, but it's not certain to be near zero.
The uncertainty principle now just boils down to the statement that the product of the uncertainties of the square of a function, , and the square of its Fourier transform,
, is always greater than some constant. In what follows you’ll find some useful stuff such as Plancherel’s theorem and Cauchy-Schwartz.
So, there’s the Heisenberg uncertainty principle: . A physicist would recognize this as
. The difference comes about because the Fourier transform that takes you from the position wave function to the momentum wave function involves an
, and
. (For the physicists out there who were wondering what happened to their precious h’s)

![Probability S[N,K] of a streak of K or more out of N independent coin flips.](https://www.askamathematician.com/wp-content/uploads/2010/07/ProbOfStreak.jpg)







