Physicist: In a flat space local ideas about “parallel” and “perpendicular” are global. That is, if two lines are parallel, and you follow them for a while, then they’ll still be parallel. (By “flat” here I mean exactly this property, parallel is parallel forever. Not just “flat like paper”. So you can have 2-d flat space, 3-d, 4-d, whatevs)
An example of curved 2-d space is the surface of a ball (just the surface, don’t worry about the inside and outside). If you draw two parallel lines on the ball, then eventually they will cross. The curvature forces the two lines to come together.
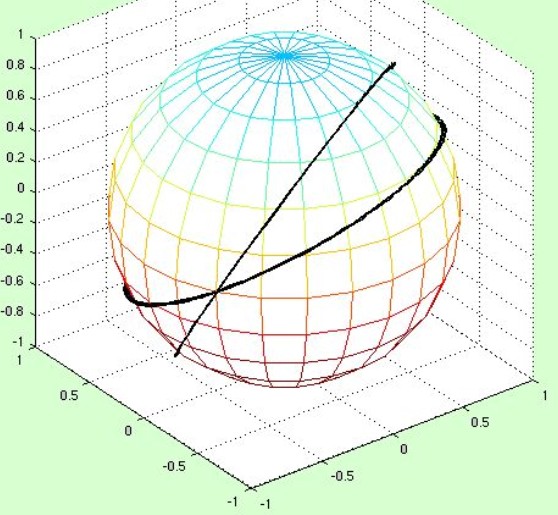
A straight line on a sphere always traces out a "great circle", like the equator. These lines are parallel twice, but also intersect twice.
If an object is not experiencing any force, then it will travel in a straight line through space. This is true for space-time as well. So if you’re sitting still (traveling forward in time), and no one applies a force to you, you’ll continue to sit still (travel forward in time).
Now imagine two people hovering above opposite sides of the Earth. I say hovering in place because this means the lines they trace out in space-time are (initially) parallel. As you run time forward you’ll notice that, even though no force is acting on them (don’t say gravity) and they are traveling in straight lines through space-time, they still move together (fall toward the Earth).
This is due entirely to the Earth curving space-time around it. Literally, it takes the original “flatness” of empty space, and curves it. It’s a little more complicated because the time dimension and the spacial dimensions are fundamentally different, but not as much as you’d think.
Another, slicker-sounding way to describe gravity is: “Things fall because time points a little bit down”. That’s not creative prose, I mean that literally.
Pingback: Q: Why does “curved space-time” cause gravity?: A better answer. « Ask a Mathematician / Ask a Physicist
I’m not sure i follow this explanation. It’s simple to see that you can have two parallel lines on a globe too. The difference between a ‘curved space’ and flat is that they will look different when ‘folded out’, but I can’t see why they should cross each other?
Drive you car around the globe and you will get two ‘parallel lines’ that never meet, from your wheels. Then imagine that you flatten out that globe, would those lines now cross each other? I don’t expect them to?
Do you?
It doesn’t seem right?
You can’t state that you have parallel lines if they intersect each other. Either you are right, and then you have defined a axiom that states that there are no parallel lines as they all can be made to cross each other, depending on how you fold ‘space’, which in a way makes sense, but not when comparing a globe to a two dimensional surface.
There’s a trick to it I’m sure, a certain kind of definition you set, but it’s not my understanding of parallel lines.
Yoron.
And what do you mean by a curved 2D space?
A bent paper might be defined as ‘curved’, but only when looked at from a 3D perspective. If I was to draw parallel lines on that paper, before bending it I do not expect them to intersect. And from the perspective of someone living on that surface I do not expect it to be seen either?
I think I can see what you’re getting at, but it’s easier for me to imagine ‘space’ as something plastic, with gravity as the metric ‘shear’, acting in it. I can understand that it’s tricky to describe it in words, from a mathematical standpoint, but there should be some way to make the idea more understandable. And with that I just want to state that I do not hold you responsible, you have a lot of companionship:)
That as I’ve seen similar definitions at several places, using a globe, drawing lines, comparing them to lines of longitude, and then stating that they will ‘cross’. But lines of longitude is a definition made to fit two ‘points’ (south and north pole) where they meet as I understands it, and are no explanation of why gravity would make parallel lines cross to me. Also it seems to me that if I was to draw two lines in space following gravity they would not ‘cross’ each other in any point, they would cross in the same manner as a bridge cross a river, not meet in any point, if you see what I mean. That a triangle won’t hold in a 3D reality is quite clear to me, but parallel lines crossing each other like as I seen described is not.
(ranting a little:)
Cheers
Yoron
@Yoron (last two)
Subtle point!
If you start walking in a straight line on the Earth (a perfectly spherical Earth), then eventually you’ll come back to where you started. More than that, your straight path will have divided the Earth exactly in half. Mathematicians like these paths so much they call them “great circles”.
You’ll find that the only straight paths on a sphere follow great circles. As a extreme example, imagine walking around the north pole at 89°N latitude (1° from the north pole). You’d be hard pressed to find anyone who doesn’t agree that you’re walking on a curved, not-at-all-straight, line. A more subtle curve could be found by walking around the Earth at 1°N (just above the equator). This looks like a straight line, and it’s very close, but it is slightly curved. If you were to walk along it you’d have to continually turn just a little north (like with the 89°N path). A quick way to see that is to remember that a straight line on a sphere divides the sphere in half, and 1°N doesn’t quite do that.
So the car tires in your example don’t quite run parallel. Given the chance (on a perfect sphere) they would eventually run into each other (90° around the planet). You don’t notice the effect because, while science has determined that the Earth is round, it has also determined that it’s not that round when you’re up close.
One of the more mathy way to talk about curvature is to look at the ratio of the circumference to the diameter of a circle. In flat space you always get pi.
In “positively curved” space you get something less than pi. For example, if you take the equator as your circle, and a line that goes through the north pole as your diameter, you’ll find that the circumference divided by the diameter is 2 (less than pi).
In negatively curved (hyperbolic) space you get something larger than pi.
So, in your example with the paper (beautiful example, by the way) the geometry on the paper stays the same even if you bend or fold the paper. Specifically, if you draw a circle, you’ll find that pi is 3.1415…
Stretching is a whole other thing though. Stretching is how you go from a flat piece of paper to a piece that’s curved like a sphere, and that’s the kind of stretching that gravity does to spacetime.
So….
Space can be stretched and the more it stretches, the more “time” (length) there seems to be….
Yet mass is never changed…. but then that means it’s slowed down….
but if something is slowed down, but in only one part of space…. then space really isn’t as flat as we are used to understanding the word flat…
mass, time, space… it’s like without those three, there wouldn’t be anything….
but then…. that almost sounds like what a black hole is…. nothing…. but then it isn’t nothing…. time and mass and space has just “changed” into something we have yet to grasp….
I have just went in complete circles here ^^;
One more thing ^^;
I also see that a Tesseract could be a nice example of never ending time, space, movement?
The car example is interesting but can be explained.
Because of the relatively small size of a car relative to the size of the earth the two tyretracks can be considered as one, or alternatively the cars path is effectively a cylinder not a sphere on these scales.
If you think now about a car with a wheelbase significantly wide in respect to the earth then each wheel would need to be set to be perpindicular to the earth surface in order to be cotact the road and be ‘parallel’ in terms of a sphere. We now set them down pointed north on the equator. They are now parallel and we do not change their direction in any way we can effectively remove the connecting axle. Run the car forward and you will find that the tyretracks converge and intersect at the north pole.
My thoughts on this issue are only guesses. Problem is, I simply can’t wrap my head around gravity. While its effects have been documented for centuries, gravity is still an enigma as to what it really is. Magnetism is also well documented and has many known functions. While an enigma in its own right, scientists state that each atom in the universe is imbued with this phenomenal trait of magnetism, making them in a sense; little magnets. The asteroid belt has chunks of matter with no particular shape, yet with smaller pieces of matter orbiting around them. Why? Our moon, while being lifeless, coreless and with little or no atmosphere is still magnetic because of an atoms phenomenal power. I know there is an old saying: “if it ain’t broke, don’t fix it”. But if only to give praise to where praise is due, both magnetism and gravity should be given another close look.
Going back to the original example of two people hovering in space above the earth, the bit I’m struggling with is how the curvature in time causes them to move towards the centre of the earth. More specifically, they start at a fixed point in space, no velocity, and I can accept that time flows at a different rate for them than someone further away, but I can’t see how this translates to them accelerating towards the centre of the mass
Curvature always involves at least two directions. For example, if you have a string (one direction) and you curve it into whatever shape you like, then without changing the string you can straighten it out (in one direction, “curvature” isn’t a thing). By comparison, if you take a curved rubber sheet, like half of a rubber ball, then you can turn it inside out and bend it, but without really stretching it out or tearing it you can’t make it flat (in two directions, curvature is a thing).
The same holds true here, the curvature of spacetime is in both the up/down direction and the time direction. The curvature of the surface of a ball means that traveling in one direction soon leads to traveling in another. The curvature of spacetime near a massive body means that traveling in the time direction soon leads to traveling in the down direction. Even if you have no “ordinary velocity”, you’ll stil be traveling forward through time.
I can see what you’re saying, but I’m not really “grokking” it, if you know what I mean. I apologise for being dense about it :-). I respond well to equations though, and working from first principles, so what would be a good term to google for to get me on the right footing.
Unfortunately, a solid understanding of this means having a solid understanding of General Relativity. A textbook (any one of the textbooks called “Gravity” or “Gravitation” should do), however this is a famously difficult field. To get a taste, search for “geodesic”, “differential geometry”, and “Schwarzschild metric”.
Thanks, off on holiday for a week tomorrow, so there’s a bit of light reading for me 😉
I’m struggling with that acceleration bit.
The fact that space stretches and time vector pointing to future bends towards mass is all fine and i can see it working. But..
If i hold a small object in my hand (i can only lift small objects:)) and let it go. Then this object has an inertial given by earth rotation so (simlified) without time pointing “down” it would just fly of on tangent. That time and “more” space “down” makes it travel towards Earth, so far so good. But what makes it accelerate towards it? Is it that stretched space? But this would be impossible to detect from the “same” space.
In different words: I see how a change in geometry creates a path for an object to travel along with no external force acting on it. But i don’t see how any change in geomentry of spacetime can make it appear to accelerate in my (the observers) frame of reference.
Is that acceleration given by spacetime curvature difference from “point to point”? E.g as it’s increasing “downwards” it makes it look like the ball needs less and less time to cross the same space distance? But this would mean that any object would need to pick up “starting” downward pointing Z speed vector practically instanteniously. That Z speed would be given by the spacetime curvature at the point of a drop, e.g. it’s distance from Earth. This is of course not the case in reality as all objects gradually pick up Z speed from 0 as a function of g.
Am i making any sense with this question:)?
Ok, Here’s an option how to explain that acceleration bit:
it kinda comes down to a fact that free falling object doesn’t feel any force acting upon it (until it hits the ground of course) but accelerates nevertheless.
So it must be the spacetime itself moving, and accelerating downwards, in which the object is in fact “at rest” But then again it would mean that mass makes spacetime not just to curve but also to accelerate downwards. As if sucking spacetime in. Actually no geometry change is neccessary any longer appart from linear stretch. That linear stretch to me also nicelly explains time slowing down in vicinity of masses and the fact that spacetime is “torn apart” behind even horizon of black holes and hence GR breaks down behind even horizon.
Also if i hold a ball in my hand that ball actually does feel force even though in my reference frame it’s at rest, but in relation to the accelerating spacetime it actually accelerates upwards, due to the force of my hand.
Now what would be a mechanism for mass to stretch and accelerate space?:)
PS: “In different words: I see how a change in geometry creates a path for an object to travel along with no external force acting on it. But i don’t see how any change in geomentry of spacetime can make it appear to accelerate in my (the observers) frame of reference.”
Check out this animation explaining exactly that:
Yes, thsnks, i see that, as i mentioned i understand how curved space can make object to appear to travel without any force giving it an initial push and yes that animation shows that. But the falling apple there doesn’t accelerate:).
To me the only option is that time is “curved” as well because space curvature alone simply cannot make any object appear to accelerate with no axternal force acting on it (and yes when we are in a free fall and accelerate we indeed don’t feel any force). E.g. the time is 4th axis along which it’s possible to move any direction, same as along any “ordinary” space axis (the fact we, in our 4.6% of the Universe that we can observe, can move in one direction only and we remember past but not future is another topic i guess..).
Which kinda implies that what we call “time”, e.g. a termodynamic arrow of time, or cosmological arrow of time (the both happen to point the same direction), is not really a “real time”, but rather a product of what we are capable to observe. Which in turn comes back to the whole special relativity since it uses termodynamic arrow of time to build its model. Hence it models what we observe. However, is what we observe “reality”?:)
In other words: Seems like our models based on our observations tell us that what we observe is a product of what the model needs to explain itself. Having admitted that what we observe is a product of our models explanations, how do we know that what we observe is not an illusion? Possibly given by a fact that we’re somewhat “hardwired” to observe stuff certain way? Then our models would be totaly off mark, even strengthening our illusionary view via technologies and mathematical proofs…Ok i know…this is beyond science, and very off the topic:)
PS: “But the falling apple there doesn’t accelerate”
It moves through space the same way in both models. Go to 1:00 where you see both. On the left you see that the line slope (=velocity) changes, so the apple gets faster. The right apple moves the same way.
PS: “To me the only option is that time is “curved” as well”
Yes. In fact, that was Einstein’s initial idea. The spatial curvature follows from this, because you cannot have just one curved dimension. “Time is curved” means that the distances along the time dimension vary with the spatial position, just like the animation shows.
PS: “because space curvature alone simply cannot make any object appear to accelerate with no axternal force”
It can, if the object is already moving through space. But it cannot make it start moving.
>It can, if the object is already moving through space. But it cannot make it start moving.
But the “rest” is only a relative to the observer, so if, as you say, in my frame a body is at rest relatively to me, then it cannot accelerate in any other frames, unless i accelerate with it, because then it would start moving relatively to me. Hence the apple would never start falling.
Also the “slope” analogy doesn’t relay work, because for it to work one needs a force upon the body “pulling it down” to make it roll down the slope at the 1st place, plus the reactional force from the slope’s surface making the body not to fall through, but rather follow the slope’s surface. Without these two forces the body would just stay put no matter any curvature of anything. So even though the animation shows increasing slope no body would in fact move. Hence, as you say. the body wouldn’t start moving, but in fact we will observer it accelerate.
That’s why to me really the only way out here is that the time is a vector curved as well in a sense that it’s bent what we call “downwards”. That way we would see a body accelerate as it propagates through time with us and there is no force acting upon it (whereas there is a force acting upon our feet as we observe the apple). But if a time is a vector having it’s own axis (4th dimension in the 4 dimensional spacetime), then we have a problem with our observation. Because we don’t really observe a time as any axis, we observe it following 2nd termodynamic law e.g. in a “direction” of raising termodynamic entropy. If we do have a problem with our observation then all our “proof by observation” framework is flawed.
So to me there’s plenty of things they don’t add up somehow:)
Pingback: A simple test for the EU people. - Page 68 - Christian Forums
Pingback: Q: Since the Earth is spinning and orbiting and whatnot, are we experiencing time wrong because of time dilation? | Ask a Mathematician / Ask a Physicist
If the parallel lines have to meet in a spherical space then all the objects that travel from equator to North of South pole would have to converge to become a point. Is that the case? I don’t think so.
1. How can matter such as the sun bend empty space? Only things or materials can be bent – you can’t bend nothing then call it bent? That has no logic. It may act bent in an equasion or you may be able to make a formula to describe how it seems to bend space but lets get real you can’t bend empty space. By definition there is nothing there.
2. Even if you could bend space with a large mass such as the sun then it will be bent evenly all around it. The image of bowling ball sitting on a “rubber mat” is really inaccurate because it looks like the ball of the earth would fall toward the sun (this fools most people I guess) but in fact there is no gravity well as space would be bent evenly all around the sun with wells going equally in all directions toward the center. This again makes no sense as you can’t bend the same bit of space in different directions an infinite number of ways because now there is no bend in space just back to an even grade of gravity – that is not yet explained. Except that it acts as if it bends space or perhaps it is better to say: “It can bend light” that is why we see gravitational lensing. Light has a particle so it can be pulled on.
3. Even if there is a gravity well in one direction and there isn’t as in #2 above this still does not explain the force of gravity as one still needs to explain why a large body such as the sun could attract the earth when the earth is on a slope of curved space. Lets say the earth is in a fixed position from the sun. No rotation around the sun. The force that pulls it down the slope is what exactly? It can’t roll down the slope as it has no weight in space. If that was true the whole universe would be falling and we would know this because the things on the top would be lighter (or fly upward) than the objects on the bottom of the earth – say in Antarctica heavier (pressed toward the earth). There is no weight to the earth in space only gravity to pull it toward the sun but no one has explained it yet. I think we should just admit that and look for a better theory than mass bending space. It may seem to bend it and we have a formula that works to explain the things it does but that is not the same thing. Heat from a fire makes me feel warm, that does not explain the physics of kinetic energy. Weight that I feel when I pick up an anvil is not explained by curved space or time as I am at rest (nothing is moving). A topographical map does not explain how mountains form. Gravity creates a sense and measurement of weight when I hold an object – why would curved space and time give one this sense and measurment?
Also Einstein does not explain how a mass like the sun can bend empty space – even if it could. That is just magical thinking.
As something always has to come from something else; we need a better theory.
Why does the area of a black hole remain constant?
Curved space does not cause gravity because curved space is a metaphysical absurdity since space is a vacuum. The idea that curved space causes gravity is an absurd attempt to explain gravity that must be the result of the belief that photons have no mass. It would be better to suppose that the energy of photons are pulled by gravity than to pretend to have explained gravity by curved space.
Pingback: Which Way Is Down? - What is it
Pingback: Which Way Is Down? | PHP Video Academy
Pingback: Which Way Is Down? - Too long; Didn't watch.
This was a very enjoyable read. I don’t really subscribe to the existence of particles or massive objects. I think our observance of such things are just measurements of the net result of other phenomena at a specific instance, which now makes me wonder, what exactly is an “instance”? Anyway, I’m thinking gravity may be one type of those net observances because of the proximity and nature of the other phenomena which “generate” it for lack of a better term. Our toughest problem is that we have to “freeze” things to take a measurement in order to conceive. Imagine if you froze the playback of a piece of music in order to make an observation about it, what would you hear?
To add to the list of interesting commentary above, there seems to be some speculation about how the Hawking radiation released from a black hole is the bubble in which our holographic galaxy exists, thus explaining where the information that disappeared inside went to…
It’s sad to see people entertain the idea of space bending. Space is empty, it cannot bend. It’s disgusting and evil to carry this lie. I feel like I’m living in an Idiocracy. They are claiming you can bend a dimension which would imply it has resistance but as a prior commenter said it would bend in every direction and have equilibrium just like some object displacing water and nullify any pull as erroneous.
Just because you can make “math” for it doesn’t make it true in math I can exchange A for B as long as I replace B for A so switching things like time or movement or space can be done in math even if its meaning is pure nonsense in reality. Its just using time travel to cheat your way out of things you were too lazy to solve with fluid dynamics and basic physical movement. I can make math to show Shrek flying through the sky, it doesn’t make it true.
Furthermore and even more importantly, particles do not “time dilate” and time is not a prostitute to whore around so you can in your sick mind believe there is infinite universes. Even the act of so-called time travel in any computer simulator would require copy and paste of the universe to accommodate the new timeline violating and raping all laws of thermodynamics.
The time travelling electron theory based in relativity was created to avoid admitting that the atom is filled and surrounded by more than just a 1:1 relationship of protons to electrons… fluid dynamics can explain this by an equalization of pressure. Or dare I say… aether which was straw manned by mickelson morely. Yet later double slit proved aether(or smaller particles or mediums) by demonstrating waves in every scenario. But out of scientific conceit the “change the facts not the theory” motto was taken and aether or fluid dynamics or smaller particles as an explanation still ignored and a time travelling electron(Einstein , Feinman) was used to explain it. Disgusting. Time is just now, it is just memory, there is no such thing as attaching speed to time. Correlation of speed to time as relativity suggests is psychotic. Its like saying potato divided by couch is falafel. Its retarded and anyone who believes this is a sheep who doesn’t think for themselves and questions nothing.
What a sad state of affairs this world is in when logic flies out the window in favor of lies. Santa Claus is more believable than time travelling electrons. And even these believers in Einstein reject the idea of a god or creator(regardless of what ideology or context a creator is mentioned in even when its purely diest and non-secular) yet with a straight face these hypocritical bastards will tell you anything that moves time travels. Fuck them all, they are spreading these lies to kids when simple physics can be explained using fluid dynamics and invoking smaller and smaller particles.