Physicist: 1) Pictures and math. 2) Work through and understand the “train struck by lightning” and “barn running pole vaulter” thought experiments, to better understand the relationship between space and time. 3) Pick up a book on modern physics and do a mess of random homework problems. 4) Build something that involves relativity.
As for the second question; This is one of my favorite examples of the Allegory of the Cave. Intuition is based on experience and the mental wiring we have evolved and inherited. Almost everything we interact with day to day is smaller than a mile, slower than 60mph, weighs less than a ton, and takes less than a year. At the scales we’re used to the laws of physics are fairly intuitive. Humankind spent tens of thousands of years thinking that light is instantaneous. And who could blame them? Magellan took a leisurely three years to work his way around the planet (easy to imagine), whereas light can do it in about 1/7 of a second (hard to imagine).
Gamma (
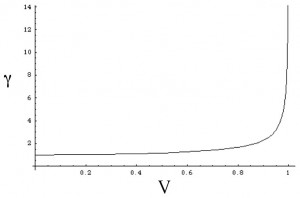
Gamma vs. Velocity. Gamma = 1 is the normal, every day experience.
On this graph the speed of light is at 
When physical laws work actively on scales we’re used to, they tend to become intuitive. The laws of the very big, small, old, hot, cold, fast, … are the same laws, we just experience a special case.
Pingback: Q: How do velocities add? If I’m riding a beam of light and I throw a ball, why doesn’t the ball go faster than light? | Ask a Mathematician / Ask a Physicist