Physicist: Scientists can generally answer “medium complicated” questions. The really hard ones are too damn hard, and the really simple ones are often “just the way things are”. Or they may be really, really difficult questions in disguise. You’ve found one of the fundamental questions that no one seems to have a good answer for. We also don’t know why the mass, 
The second half of your question we do have an answer for, it’s just a little mind bending and hard to picture. What heavy objects are bending is space itself. The way you detect space (follow me here) is with rulers or stretched out strings, or stuff like that. Anything that measures distance. Near heavy objects the distance between points is greater than you would expect, and you can use this fact to detect and measure the stretching of space.
The usual trick when trying to picture higher dimensional space is to knock off a couple of dimensions, and picture that instead. 3 dimensions is too complicated, and 1 is stupid, so here’s 2!
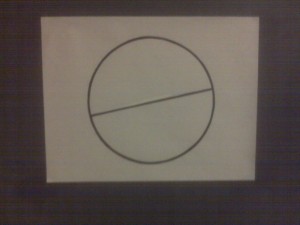
A circle and its diameter in flat space. Here D=6.5'', C=20.4'', and 20.4/6.5=3.13 ≈π.
A circle and its diameter in curved space. Here D=7.2'', C=20.4'', and 20.4/7.2=2.83<π
Take the circumference, 
That is, the diameter you get by measuring the equator and dividing by 
@munna
You’re exactly right, I should have written “spacetime”.
Q. please help..maybe I’m just thick but In which direction is space” bent “by a moving body of given mass and gravitational force ? In all the programs I,ve watched the diagrams all indicate that the moving mass tents to bend it’s surrounding near space beneath itself, which indicates that the body’s mass distorts the space beneath it.However if space itself is void of mass how can it be distorted in any direction let alone in only one direction.If space is not a true void, i.e.space is made up of some form of mass then surely a moving body travelling through space would distort space all around it.Yes I know I’m thick!!! Can anyone clarify? Thanks.
The statement “space is distorted below” is not totally accurate. I believe it is the result of how the distortion in three dimensions is conveyed to the reader/viewer. And it is typically displayed with a weight in the middle of a rubber sheet. Again, this is done to help convey the principle of what happens.
I don’t know how much correlation there is between the spacial distortion and the rubber sheet demonstrations. Therefore, take this with a grain of salt … If the rubber sheet had grid lines on it, as some images do, then dropping in the weight causes the grid lines to be distorted towards weight. I take this to mean that space is distorted towards (or pulled towards) the mass causing the distortion. So the actual spacial distortion is “towards” the mass, not “below” it.
Many brilliant minds have mulled this question over for centuries without success. Only Einstein came up with the theory of gravitational lensing which was later proven as fact, that something?, actually bends the track of photons around celestial objects but does not necessarily bend space itself. Personally I believe the innate property of magnetism in all matter will be proven as the catalyst holding the world together, one way or the other.
Kind of late to make a comment.
My explanation is that two objects (or more) filter out a bit of the zero point flux arising between them. This means there is a force greater outside the two objects that pushes them together. So there is no attractive force at play and no need to say space is curved yet every equation still works. Simple and elegant, IMHO.
If we knew what gravity was, it would be case closed. Unfortunately that statement can not be validaed as an absolute fact. Einstein gave us theory and formula to justify space/time warping with bungee balls and a springy sheet of rubber to illustrate his theory. But today, some thirty odd years after launch, Voyager and its twin are still out there in interstellar space zipping along in a straight line hopefully bound toward another planetary system. With multiple billions of miles behind them, as yet nothing has been said to alarmed us about space/time warping their trajectory. I don’t believe we have discovered everything about attraction and the status quo of planet orbital positioning or why they circumnavigate suns as they do. Of course, I don’t know why galaxies rotate around their cores either? But, having an iron core as our planet does, I can see why balls of any size and mass would if suspended on mile long cables above earth, would converge toward a central point instead of hanging straight down. They are seeking their own straight line toward earth’s center. If you dug a hole on to the center of our planet, and continued the cable length, the balls would eventually converge to a central point. Gravitational or Magnetic attraction? Take your pick.
@Orien Rigney
The motion of all of the planets, as well as all of our space probes, exactly follow the predictions of General Relativity. The Voyager probes are absolutely subjected “warped spacetime” in the form of gravity, all the time. We also understand why planets orbit the Sun and why galaxies rotate.
Magnetism is similarly a well understood force, that is definitely not gravity.
Having no skills in either physics or calculus, I can only give you my thoughts on Einstein’s theory of relativity and space/time generation. To begin with, whether we are talking about gravity or magnetism, what seems to be left out of either equation are the whys of directions and velocities. Unless figures lie; the universe, to include every single atom of it, is constantly expanding at a velocity of over 2 million miles per hour. Our own galaxy is rotating at approximately 500,000 miles per hour while maintaining this breakneck forward rush. Our sun, it has its own problems with its equator making a revolution every 26 days at one speed while the upper and lower segments rotate at a much lower rpm, taking 34 days, yet maintaining this 500,000 mile per hour trip around the galaxy. To what are these variable speeds relative? Earth, as all other planets in the solar system must maintain their variable distances and velocities as they revolve around our sun. Then we have the moons throughout our solar system doing the same as our own. I ask, to what are these variables related? Could it possibly be that relativity is nothing more than random chance combined with some very clever calculations? Our solar system has been around for roughly 4.5 billion years while slowly settling into a rut of which a battle is forever being played out to determine if our sun, planets, moons, comets, etc. will remain at a given time. This is likely the scenario of solar systems throughout the entire universe. As humans, we have witnessed only the smallest faction of thirteen billion years of random change this universe has undergone. You can make book on it though, before this century is over; what we experience as unflinching scientific fact today will have changed drastically. Oh my! To have learned calculus and physics in my youth.
Forget about space-time bending, it is complete nonsense!
When an object accelerates in space (I still call it aether) the object will experience an inertia force. Gravity behaves as if it is the same as inertia, but when we stand motionless on the surface of the Earth why do we experience gravity?
Well simply the Earth absorbs aether (space) and therefore we get the same inertia force, but now we do not accelerate in the aether, but the aether accelerates in us.
But if the aether (space) is absorbed by stars, planets, moons etc. why don’t we run out of space? Good question, so something must emit aether to keep balance with the absorbed aether from all matter bodies like stars, planets etc.
We know that there are physical forces (not only gravity) which make matter getting denser and denser so forming galaxies, stars, planets etc. but if matter has the property to get denser then anti-matter should have the property to get less and less dense, that means it will have the tendency to spread out evenly over the universe.
So yes, space is expanding by emission from anti-matter, but this is only to compensate the absorption from matter (of stars, planets etc.) and this explains the redshift from light coming from far away galaxies, travelling through expanding space. This does not mean that the galaxies are receding from us so the universe is mainly static. This eliminates completely the need for the Big Bang theory, which is full of illogical assumptions and begins even with a singularity where everything comes from nothing, in my opinion an absurdity lacking any causality!
I hope this will be a more satisfactory explanation than bending space-time!
Yes, yes yes- all brilliant stuff isn’t it! The most basic question “how did it all begin” still baffles the most brilliant minds.Yet somehow I do believe that there is a simple answer to it all! to the beginning of everything! perhaps we’re all just thinking too hard and the explanation lies right under our noses. We seem to be bogged down looking for a needle in a haystack of theories and calculations.Yet, I do believe that the answer is staring us all in the face – we just can’t see it! Where did the very first basic element come from?The laws say that you cannot produce something from nothing! Well that law must be wrong, musnt’t it? unless everything has always existed in one form or another. If the latter is true then we are all wasting our time looking for the elusive “beginning”! Perhaps there has never been a beginning to everything and and there will never be an end to everything.Perhaps everything just changes form and keeps going round in a circle without a beginning or end, never ending, for eternity.If that is the case then “time” (as far as the cosmos is concerned) does not matter.Time is just a convenient chronological method for us to measure the progress of existence, intervals between past, present and future events and occurring phenomena.Oh Boy…It just keeps going on and on doesn’t it????? Ray
I get your reasoning Ray. How nice it would be if science could be explained away so rationally. Unfortunately I’ve tried a thousand times to do so and it still doesn’t work. No! Science requires more than just a small dose of analytical Physics and Math, of which most of us are usually a bit shy. BUT!………
Me, I like to think of the bending of space and time as nothing more than the magnetic attraction or repulsion of objects as they flow merrily along through the ether. We must remember that our entire universe was regulated to “specific speeds” billions of years ago by what was the vectorially and symmetrical velocity dictation of what we “speculate” as the Big Bang. This rule holds true today unless acted upon by either magnetism, entropy or collision, of which all pay a part in random chaos.
Our mainstream science seems hardly logical and is very materialistic. We have theories like the evolution theory, the Big Bang theory, relativity theory etc. but if you go deeper in these theories these have all mayor flaws.
Calculate the chances that a life protein would form by random chemical reactions. I tried the example of a protein consisting of a chain of 100 amino acids, that would form by random chemical reactions and came to the conclusion that the odds that it could be produced was 1 chance out of 10 to the power of 250, which means impossible.
Now you may say that there is always one chance, well if this would have been the case, you have one protein waiting for ever for a second one, so forget about the simplest microbe (by the way there are no simple microbes, they are all very complex).
Now the Big Bang theory, which says the universe started 13,7 billion years ago.
With powerful telescopes we can see galaxies at 13 billion light years distance. So these galaxies cannot have an age beyond 700 million years. In this 700 million years it traveled 13 billion light years that is with an average receding speed of around 18.5 times the speed of light. However we can see the galaxy so after 700 million years the speed must have reduced to just under the speed of light, all rather bizarre. Moreover we can see galaxies at distances of 13 billion LY in any direction, so are we in the centre of the universe?
In particle physics we have elementary particles (this means these particles are not composed of other smaller parts) one elementary part is the electron with an electrical charge of -1 an other particle (anti matter) is the positron with a charge of +1, other elementary particles are quarks with charges of 1/3 or -2/3, how can an electron be an elementary particle if 1/3 and 2/3 of the electron or positron charges exist?
Einstein bases the relativity theory on the supposition that the speed of light is a constant and nothing can go faster than the speed of light. Why does a black hole still attract matter around it although light cannot escape from the black hole.
All valid questions, so our science is far from perfect and some fresh thinking would do good for the future of our science.
Real science should also include spiritual observations, by only concentrating on material science and exclude spiritual phenomena as humbug and not worthy of science, is a grave mistake.
Nothing can bend space as space is a vacuum, I do need to give any fanciful exquations or theoritical jargon but just plain common sense. If space is a vacuum where there is no medium I.e a void then common sense should tell you there is nothing to bend. These theories are just theories as they have no been proven. The scientific world is now sadly based on falsehoods that violate all common sense and logical reasoning. We live in a world where critical thinking is severely lacking, how can a beam of light travel thousands or million miles from a source to light a distant planet or object when logic dictates that it is illogical. For if I enter a dark room devoid of any light and have mirrors on every part of the four walls and take the strongest torch I have, if I turn on the torch and turn off it off the light disappears immediately. The light of the torch is not travelling around the room once the source disappears, this is common sense that a child can understand, so why is this false doctrine being preached when it is quite clear false. The theory of gravity as currently taught is another falsehood as common sense and reasoning tells us that it is not attraction for if it was the moon would come crashing towards the larger object of earth, if I have two objects on a flat plane the smaller object will not slowly start moving to the larger one as if by magic. Please start being more critical and stop believing falsehoods that by the own eyes and logic are false
Well the comments section is clear evidence that 100 years of General Relativity hasn’t filtered down into the schools education system properly yet. What a load of rubbish about Ether of Magnetism or relying on “common sense” to figure out the most complex issues we face. Best evidence of confirmation bias I’ve read in a while. To the actual question “Why do heavy object bend space?” the answer is currently unknown. It is a big question that we are working on. But to all the numptys with their wild speculation, we do know that it does happen – we have observed it happening. For 100 years every prediction of General Relativity that could be checked by experiment has been verified as correct. What is happening is that big amounts of energy (mass being a suuuuuuper concentrated form of energy) do bend spacetime. Spacetime is the fabric of the universe itself. If you get rid of everything else, there is still spacetime. It can bend and stretch and twist and ripple. But how energy does this is the hard bit. We just don’t know the interaction that does it. Possible explanation is that there is a gravity field throughout the universe that has graviton particles that are interracting with other particles – but we will never be able to build a detector to measure them to test this. So we’re relying on spotting other predicted effects, like gravity waves.
Because the whole hypothesis is all wrong, heavy objects do not bend space, what they do bend are trajectories and distances between objects, but not space itself-that’s a huge difference.
First of all space-time does not bend at all, what does bend are electromagnetic fields and energy. There is no such thing as space in entire universe, if you get rid of everything else you will not have spacetime, because everything would be 100% empty-we are talking about 100% and infinitely empty space.
Huge amounts of energy do not bend space at all not even the slightest, they only bend energy fields, matter and trajectories and distances between objects-facts, the fact is space does not change, because it is not made of anything.
If “spacetime” is behaving like a rubber than this is not true space at all, not even the slightest, it means it has energy and energy is something, energy is not space, energy is not time.
These are completely different concepts.
Basically, what Einstein was 100% wrong as all other physicists is the totally and 100% wrong hypothesis that space bends-no, space does not bend at all, not even the slightest; something that has no physical substance and it does not possess anything physical at all in it, inside itself, cannot possibly and does not bend, only energy can bend, only forces can bend, only matter can bend, but space cannot bend at all, not even the slightest, since it is completely empty, no quantum fluctuations or anything-deal with it, people.
Spacetime is not actually a spacetime at all and it has nothing at all, not even the slightest with both space and time, it is merely electromagnetic energy fields completely interconnected with each other, the entire universe is made of electromagnetic energy/light.
And this is why so-called “spacetime”/universe bends like a rubber, it has nothing to do with space, since true space does not interact with anything at all, since it is completely empty, it is electromagnetic energy fields as well as quantum EM energy fields that are interacting with each other and make look like “spacetime” is bending-100% irrefutably 100% proven facts.
The same facts are unchangeable with the contraction and expansion of universe.
You have to realize that there is no such thing as space in the universe, the entire universe is made of light and electromagnetic energy, which by itself 100% proves that universe itself and everything inside the universe itself does not have/does not possess space at all, not even the slightest, inside itself.
Also, the true space cannot be detected since it is 100% empty and it does not interact with anything at all, ever, not even the slightest-100% irrefutably 100% proven facts.
Dear Mr. Physicist,
Ok, I would like to make a 2d space , 1d time, software model of a 2d disk earth (as in the Planiverse, the technical and logically without contradiction, sequel to Flatland) orbiting the sun, with metrics, from GE explaining the accelerations. Be nice if a dip or bump of parabolic shape is apparent, if i slice the timeline from the side, where Time is like X on a graph, and we see Y, a projection of some motion. With 3d being all of spacetime, time is frozen and we are examining a static 3d model. If I turn on animation, we see moving orbits from the top, orthographic view. If I turn on animation+ spacetime visualization, i expect to see the past, then the present and sort of a glowing slice at T= x…, and the future as a nice continuous shape. An orbit of disk planet, will be smooth spiral spring i could 3d print and hold and pet and adore. Time would just be an illusion. The creatures on the planet would remember the past and have yet to learn of the future, but its all there for us 3d beings. Cool, we should be able to understand everything, we are beyond life and death for him, like gods. But, no,not so fast.
I am trying to understand this General Relativity model like everyone else who has seen the video with the guy and the rubber sheet and the billiard balls. Again , Stepping down to 2 + 1 spacetime. So, I read that in our spacetime, the timelike component (orthogonal to x, y, and z planes, incomprehensible to us) is bent more than any spacelike dimensions, toward or tangential to the object being orbited, and that is part the explanation of Newtonian gravity ( never minding black holes or extreme curvature). Take the 3d objects on the rubber sheet, pretend they represent 2d objects. Many viewers are disturbed, it works because earth gravity is pulling it all down. What if you put that apparatus with an upper and lower layer, in rigid transparent plastic, into zero G.. now will there be orbits? I can see the bulge pushing away stuff.. and that means it putting into the bowl on the other side of the sandwich.. Things seek the path of least action? Shortest route? Locally straight lines? I’m not sure what would happen or what principle or extension of inertia is required to understand or predict. I define understand as able to predict, say.
Now if I take a flat plane an put a dent or a bump in it seems the dent will pull in stuff and the bump would repel, but that’s only with a force underneath, as the case of the experiment gravity visualized. Now , lets say the plane with the dips in spacetime is moving away from the dips.. the bottom of the dips is toward the past, so would that account for things attacting, toward the dips since time is pinched toward where they have been ? its not clear to me. If I take a x, y data, with stuf in motion, and extrude the movie in 3d , i have a nice continuum. But if I bend the x, y space into the Time dimension ( this is bent spacetime) , that is supposed to be orthogonal, i’m very confused, especially if this is for every day orbits. my movie data is messed up.. I can’t even know what time is if I take a slice with a guillotine. Even on a simulator, i have a 2dWorld simulator, i can extrude it to 3d, but I have made no attempts to model gravity. I put Newtonian gravity, fine, and there is no need to bend space. But, I have no causality. Spooky action at a distance is ok with me , but not with Einstein, who is right about alot of stuff even now.
I’m more spooked by my T getting mixed with my X, Y.
But, as tesla said we should think in terms of waves. in the frequency domain. OK. At this scale, i don’t know, but ill try. No, waves do not help. Except that light is a wave with a constant speed for all observers. Einstein said it, i believe it as a given for now.
So, how about relativity.. Different observers are going to need to agree at these speeds. Ok, acceleration being equivalent to gravity. There , that might be my ticket. Acceleration involves time, and has parabolic shapes. So if I put the acceleration potential field as a dip, things aren’t going to go back in time.. but they will find the progress forward in time easier with this gradient, let me say, a field gradient. I conclude the curvature in time would be very small as well, but, this is a very weak force, and if space is bent, that would affect even a giant planet. Also, since light takes 6 minutes to go to mars I believe, curvature into the past and relativistic effects are macroscopic on this scale. I do wonder how much of a curve I would put for say the sun, in relation mars. How bent, how many hour or minutes deep is the parabola, if i disregard any space contraction. If time is dilated approaching a mass, this puts my dip in time, out towards the future, correct?
and I wonder if using bent 2d +1 spacetime could be a visual model gravity for 2+ 1 space, that is better than the video on youtube with 2 million views and as many comments. I could put the 2d universe as a skin on a sphere ( an expanding universe for the Planiverse denizens, and have it expand, so a the past, or a dent would be toward the center, i’m guessing. Normal to the surface is a direction i can keep organised. We have no repelling objects in space, and a bump might violate causality? Or would it.. I have the software tools to create this, but I don’t feel my rigid 2d bodies are going to naturally fall into that parabolic dent, unless I know a bit more about these metrics and code them to do it. I would just try if Im told im not clueless about the shape of spacetime, how much to bend it, in what direction, and how to relate distance to time. Minkowski gives a clue that space would move at the speed of light in a vacuum? That would keep my time dimension sparse enough, i suspect. I’d love an answer but im looking at https://www.quora.com/Relativity-physics/How-can-space-time-curvature-be-explained-in-laymans-terms and worldlines that are all squiggly on Wikipedia.. each depending on an objects velocity relative to the gravitational source , i presume. Sorry for such a long post, I am showing my thinking process so you can see how the confused think, for teaching purposes.
I m an mechanical engineer ,not a cosmologist nor a astronomer but have given much thought about heavenly bodies bending the fabric of space ;Does this mean that all space needs to be horizontal ( like a flat rubber sheet ) ? If this is true , then why do we see all galaxies not in a flat plane but at all different angles to the milky way ? Does this mean that Einstein’s theories are all false ?
I would like to have a clear picture in my mind about how this really works .
It is easier to understand space curvature near bodies if we think of fourth space (not spacetime) dimension. The mass positioned in any point if 3D space spreads to the fourth dimension in this point. No mass – fourth dimension has zero size (in this point). More mass, more fourth dimension spreads. It is like to say that mass is pushed away from itself in fourth dimension. If you have a light particle in a point, it is like a rod of certain length spanning in fourth dimension from thus point. If the particle is heavier, the rod spans more. So a planet would look like a 4D structure spanning in the fourth dimension most around the planet center. This fourth dimension we cannot ‘feel’, but the more it spans around us, the more our 3D space is curved. I.e. the light and any other particles move differently in our 3D space because the fourth dimension makes our 3D space curved – similar to how 2D sheet gets curved if you place a heavy object on it.
The first fundamental problem above is the people don’t all appear to be fully informed. I know I am not fully informed, but I am a physicist, and informed enough to recognize plenty of thought errors.
The second fundamental problem I am seeing with the writings so far is that people don’t understand that “space” is just a word, and a word means nothing until you attach a meaning to it. In the context of Newtonian physics, the meaning of “space” or “space-time” is pretty simple, but Relativity begged to assert that this simple Newtonian model breaks down under circumstances. What this means is that under those circumstances, the word “space” needs to be redefined, and when Einstein said that matter bends space-time, he wasn’t just saying that the classical model of space and time was bent .. he was saying that space and time need a new definition. He was also saying that his proposed new definition of space and time would agree with the measurable appearances from a classical perspective of space-time appearing to be bent. So, to begin with, it’s nonsense to assert in the face of einsteinian mechanics, that his definition didn’t work, because the math has not yet been shown to be false (that I know of). The fellow multiple posts earlier with the 700 million year old galaxy was making blatant math mistakes, in case anyone noticed. It isn’t nonsense at all to assert “hey, I don’t like Einsteins definition of space and time”. That is a matter of choice, and it isn’t really possible to prove that a word has to have a specific definition. In any case, Einsteins models are consistent with measurements, and that can not be taken from him without showing a circumstance under which his equations don’t hold. Simultaneously, Einstein never said that I know of what space-time actually is. He merely showed that certain math models work.
Anyone can appear on scene and propose definitions for space and time that he/she prefers. That individuals equations may or may not hold up to observation as well as Einsteins. In any case, a definition for space and time doesn’t have to refer to anything about reality to be a real definition. This is one of the primary conundrums of mathematics. Mathematicians regularly operate equations that have no known connection to reality. There is no proof that reality is completely scalably/translatably reasonably described by any n-dimensional real/imaginary number model, or any existing number model at all. It’s very important to understand that math and reality are relatable, but separate, something like a map of China is not China. Real physicists don’t really tell people what reality is … they merely create math models that correlate strongly with observations. Furthermore, multiple math models that appear to be different on the surface can often be proven to be the same model, once word definitions etc. are carefully accounted for. In mathematics, we do a lot of conversions between different formal systems. In the end, without being somehow privy to the underlying system, it is impossible to determine whether one model of underlying system is in operation, or any one of an infinite set of equivalently behaving models. Therefore, the physicists neverending quest is to gain access somehow to details of underlying systems, such as to discriminate between competing models.
By now, It becomes apparent at this point that models of space-time need to be identified with their creators. In this way, we can identify Einsteinian space-time, which he derived primarily out of the Michelson Morley experiment which disproved the existence of Michelson Morley Ether, and later on the behavior of gravity. Michelson/Morley did not disprove all possible models of ether, and Einstein did not disprove all other possible models of space-time. Michelson Morley ether was basically assumed to be a fluid with uniform, velocity something like water or air. Access to the dark matter concept already breaks the notion that fluids must have uniform velocity. If dark matter does not interact, then there would be no reason for locally uniform dark matter velocity. Hence, a model of Ether that may work would be one of a disassociated fluid where the fluid particles not only don’t interact with one another, but also exhibit all possible velocities, therefore creating a medium in which there is no preferred velocity, as relativity demands. I have not worked enough equations to assert that such a model is viable.
What is bent? Einsteinian space-time .. not every possible definition of space-time. In Einsteinian space-time, there are no absolute coordinates of either space or time, but rather an infinite set of competing frames of reference. Einsteinian space-time is defined by the observations he used to build the models. That means that his space-time is defined by light trajectories, object trajectories, time measurements, acceleration of gravity etc. and his models math holds with observation. What is bent that is measurable? Trajectories. Things behave as if they were attached to a backdrop of bent space-time, meaning that trajectories that are locally straight appear from other locations to be bent. In other words, Einsteinian space-time has no consistent/universal frame of reference or definition of straightness. Therefore, relativity is normally described as a comparison between a pair of disparate frames of reference. What Einstein said is that trajectories appearing locally to be straight can appear from elsewhere to be crooked. Measurements of time and space depend upon velocity, acceleration, and gravity. The twins paradox is the paradox that brings us to the conclusion that acceleration/gravity are actually parts of measurement as well as the more commonly considered velocity vector.
I believe that acceleration/gravity was included by Einstein in General Relativity while special relativity only included the velocity vector into the calculations. Special relativity crashes on the twins paradox while General relativity does not. Junior level physics that I know of only describes special relativity while general relativity may be reserved for those who wish to seriously pursue theoretical physics.
Someones above description of ether sounds like it’s inconsistent with Einsteins theories because the fellow used the word ether. However, we must remember that Michelson Morley ether is not necessarily every possibly meaningful definition of ether. Therefore, there is no immediately apparent inconsistency between the idea that non-Michelson-Morley ether is both produced and consumed by matter and/or anti-matter, or perhaps non-michelson-morley ether creation zones. Remember, there appears to be no law of conservation of space-time. Space-time and/or Ether, not being matter, do not interact with conservation of mass/energy laws, and may as such be allowed in our equations to be created/destroyed or injected/ejected into/out of the system at will in any way such as to satisfy the demands of a mathematical system. When we decide upon a set of equations that uses the words ether/space-time, we simultaneously create a definition of such, separate from Einsteins definition, and there will be an appropriate mathematics that is able to relate Einstein space-time to Joe Schmoe’s Ether model, so long as the ether model also agrees with known observations.
What might a non-Michelson-Morley ether actually be that is consistent with all observations? Someone might have a good answer to that, but as of yet, such an answer has not dominated the science community.
I am not a physicist, so my question can look naïve to professionals.
If we speak of curved 2D space, like the surface of Earth, the space is curve because there exists the third dimension, i.e. because the actual Earth is a 3-dimensional ball.
Now, would it be not natural to assume (just for the purpose of visualization or understanding) that in our universe there is a fourth dimension such that normally all of the substance (i.e. particles) have the same coordinate on this dimension (e.g. zero) and only if in some place there are many-many particles together, they start extending to the fourth dimension? [This fourth dimension has nothing to do with the fourth dimension of our space-time, i.e. it is not time, it is an additional dimension of the space].
So if you could place many-many particles in exactly the same place of our 3D space, they would actually spread in the fourth dimension to create kind of a rod. And by this way, our Earth is actually not a 3D ball, but a 4D ellipsoid.
If this were true, it would be natural that the more massive body you have, the more it is spread in the fourth dimension and this way our 3D space is more curved – similar as a bed sheet is curved more when you place heavier objects upon the bed. (Black holes could be spread in this fourth dimension very-very far).
Now perhaps it is possible to propose a model of forces and movements for this fourth dimension, kind of law of attraction and repulsion between masses. Maybe at close distances (i.e. in the fourth dimension) particles are more repelled from each other and at further distances the attraction is stronger, so the masses keep together, but not too close.
Perhaps this low should also depend on the speed, so the particles will not oscillate forever (or maybe they do oscillate and it is allright).
And this law should be such that the integral influence of the whole universe’s mass keeps all particles of the universe at the same ‘plane’ in this 4D space, but when much mass gathers together, the effect of their repulsion is strong enough, and the mass starts sticking out of this plane.
I am wondering if any model like this has ever been considered.
The fact that our space is curved not just because-there-is-mass-around, but because this-mass-goes-into-the-fourth-dimension, does add natural and common sense ‘feeling’.
(I realize though that physicists say that physics is ruled by mathematics and there should not be any common sense or ‘feeling’ if equations are proved by experiment).
I can’t comment of whether or not physicists have considered such an idea. (I am not a physicist.) However I do see a minor flaw in your proposal.
I do not think the shape of a three dimensional object would change by taking into account an additional dimension. I base this on what we can observe by moving an object with zero, one or two dimensions into an environment with one or more additional dimensions. For example, a point (a zero dimensional object) is still just a point when considering one, two or three dimensional space. Likewise, a line segment (a one dimensional object) is still just a line segment when considering two or three dimensions. The same goes for a circle (a two dimensional object), which is still just a circle when taken to three dimensional space. So, I think the earth would still be a sphere when adding a fourth dimension.
I do not think it should be assumed that the entirety of an N dimension object is at the same location within the N+1 dimensional space. I also base this on observation. If we take a circle defined on a plane with X and Y coordinates, it is an assumption that this plane is the same as the X-Y plane of three dimensional space. We make that common assumption, when in fact that plane is merely one of an infinite number of planes in three dimensional space. Moving an N dimensional object to an N+1 dimensional space tells nothing about the object’s location or orientation within that additional dimension.
“I do not think the shape of a three dimensional object would change by taking into account an additional dimension”.
It is not about changing shape of a 3D object when it moves to fourth dimension. The 3D object may already be a 4D one and you only see it in 3D, as you have no access to the fourth dimension.
It is about when many particles are placed at the same point in 3D space they spread in the fourth dimension. I.e. there is a force that acts in the fourth dimension that pushes particles away from each other in this fourth dimension.
(Well, this was just a fantasy to justify bending of 3D space, as for bending 2D space we use third dimension).
I couldn’t sleep tonight because of sciatica, googled “space bending,” and found this wonderful site. It is nice to see so many people living the intellectual life. Thank you for sharing your questions and your thoughts with me. The discussion was stimulating and helped ease my pain. It’s six o’clock in the morning so now I will say “good-nite.”
Now I have a headache. Thanks everyone.
You can not bend space. Einstein was wrong. What is being bent is electromagnetic lines of force. Please wake up.. Oh and by the way, light is not a particle. It’s a wave. A wave in the electromagnetic pool. Light = Electricity = Gravity
“You can not bend space. Einstein was wrong. What is being bent is electromagnetic lines of force. Please wake up.. Oh and by the way, light is not a particle. It’s a wave. A wave in the electromagnetic pool. Light = Electricity = Gravity”
You nailed it Jack about Einstein being wrong and ligth issues, and space bending.