Physicist: With very few exceptions, yes. What we normally call “random” is not truly random, but only appears so. The randomness is a reflection of our ignorance about the thing being observed, rather than something inherent to it.
For example: If you know everything about a craps table, and everything about the dice being thrown, and everything about the air around the table, then you will be able to predict the outcome.

Not actually random.
If, on the other hand, you try to predict something like the moment that a radioactive atom will radioact, then you’ll find yourself at the corner of Poo Creek and No. Einstein and many others believed that the randomness of things like radioactive decay, photons going through polarizers, and other bizarre quantum effects could be explained and predicted if only we knew the “hidden variables” involved. Not surprisingly, this became known as “hidden variable theory”, and it turns out to be wrong.
If outcomes can be determined (by hidden variables or whatever), then any experiment will have a result. More importantly, any experiment will have a result whether or not you choose to do that experiment, because the result is written into the hidden variables before the experiment is even done. Like the dice, if you know all the variables in advance, then you don’t need to do the experiment (roll the dice, turn on the accelerator, etc.). The idea that every experiment has an outcome, regardless of whether or not you choose to do that experiment is called “the reality assumption”, and it should make a lot of sense. If you flip a coin, but don’t look at it, then it’ll land either heads or tails (this is an unobserved result) and it doesn’t make any difference if you look at it or not. In this case the hidden variable is “heads” or “tails”, and it’s only hidden because you haven’t looked at it.
It took a while, but hidden variable theory was eventually disproved by John Bell, who showed that there are lots of experiments that cannot have unmeasured results. Thus the results cannot be determined ahead of time, so there are no hidden variables, and the results are truly random. That is, if it is physically and mathematically impossible to predict the results, then the results are truly, fundamentally random.
What follows is answer gravy: a description of one of the experiments that demonstrates Bell’s inequality and shows that the reality assumption is false. If you’re already satisfied that true randomness exists, then there’s no reason to read on. Here’s the experiment:
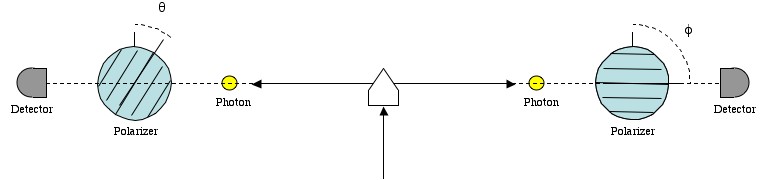
The set up: A photon is fired at a down-converter, which converts it into two entangled photons. These photons then go through polarizers that are set at two different angles. Finally, photo-detectors measure whether a photon passes through their polarizer or not.
1) Generate a pair of entangled photons (you can do this with a down converter, which splits one photon into an entangled pair of photons).
2) Fire them at two polarizers.
3) Randomly change the angle of the polarizers after the photons are emitted. This prevents information about one measurement to affect the other, since that would require that the information travels faster than light.
4) Measure both photons (do they go through the polarizers (1) or not (0)?) and record the results.
The amazing thing about entangled photons is that they always give the same result when you measure them at the same angle. Entangled particles are in fact in a single state shared between the two particles. So by making a measurement with the polarizers at different angles we can measure what one photon would do at two different angles.
It has been experimentally verified that if the polarizers are set at angles and
, then the chance that the measurements are the same is:
. This is only true for entangled photons. If they are not entangled, then
, since the results are random. Now, notice that if
and
, then
. This is because:
We can do two experiments at 0°, 22.5°, 45°, 67.5°, and 90°. The reality assumption says that the results of all of these experiments exist, but unfortunately we can only do two at a time. So C(0°, 22.5°) = C(22.5°, 45°) = C(45°, 67.5°) = C(67.5°, 90°) = cos2(22.5°) = 0.85. Now based only on this, and the reality assumption, we know that if we were to do all of these experiments (instead of only two) then:
C(0°, 22.5°) = 0.85
C(0°, 45°) ≥ C(0°, 22.5°) + C(22.5°, 45°) -1 = 0.70
C(0°, 67.5°) ≥ C(0°, 45°) + C(45°, 67.5°) -1 = 0.55
C(0°, 90°) ≥ C(0°, 67.5°) + C(67.5°, 90°) – 1 = 0.40
That is, if we could hypothetically do all of the experiments at the same time we would find that the measurement at 0° and the measurement at 90° are the same at least 40% of the time. However, we find that C(0°, 90°) = cos2(90°) = 0 (they never give the same result).
Therefore, the result of an experiment only exists if the experiment is actually done.
Therefore, you can’t predict the result of the experiment before it’s done.
Therefore, true randomness exists.
As an aside, it turns out that the absolute randomness comes from the fact that every result of every interaction is expressed in parallel universes (you can’t predict two or more mutually exclusive, yet simultaneous results). “Parallel universes” are not nearly as exciting as they sound. Things are defined to be in different universes if they can’t coexist or interact. For example: in the double slit experiment a single photon goes through two slits. These two versions of the same photon exist in different universes from their own points of view (since they are mutually exclusive), but they are in the same universe from our perspective (since we can’t tell which slit they went through, and probably don’t care). Don’t worry about it too much all at once. You gotta pace your swearing.
As another aside, Bell’s Inequality only proves that the reality assumption and locality (nothing can travel faster then light) can’t both be true. However, locality (and relativity) work perfectly, and there are almost no physicists who are willing to give it up.







True randomness = magic, ie., the very opposite of science. How do we know this? Via the works of two geniuses almost every theoretical physicist ignores- namely Godel (don’t know how to do the accent over the ‘o’) and Turing. Both are mathematicians with a vastly better understanding of the language of science than any theoretical scientist I’ve ever read.
1) Godel, via his ‘incompleteness theorems’ proved there is no such thing as ‘super’ maths. In other words our ‘language’ of maths allows the expression of all possible mathematical constructs. This may seem like a subtle point, but it is anything but. Maths is the fundamental language of science- that is to say all scientific principles must be capable of being expressed in mathematical form- tho we may lack the knowledge at any given time to describe any given known aspect of science this way.
2) Turing proved that all maths can be expressed as a computer program on a ‘Turing Complete’ machine- which is not some SF nonsense ‘super’ computer like something out of ‘Hitchkikers Guide to the Galaxy’- but a trivial combination of data storage and a few fundamental logical operations.
3) Turing Complete computers are State Machines- for any given input state there can be only one given output state.
So all ‘science’ must be expressible as a ‘program’ on a Turing Complete computer, for all science, to be ‘science’ must be expressible in the language of science- namely maths.
Now we can examine the nature of a Turing Complete computer using maths, because code and data can be made to be the same concept mathematically and compuationally. And as a result certain proofs derive from the Turing Complete computer.
It is IMPOSSIBLE for a Turing Complete computer to produce true randomness- so it is impossible for true randomness to exist in science. This isn’t even up for debate. Debate ended with the work of Turing and Godel- and beings maths not ‘science’ there is no possibility of a ‘model’ that will change in the future. Maths is the only language of science- a fact near zero theoretical phycisists ever come to terms with despite their reliance on maths.
The Turing Complete computer likewise denies the possibility of Free Will being explained in terms of ‘science’. As I said, the ‘clockwork’ universe is a state machine with each ‘new’ state directly deriving from the earlier one. This is the only reason science, not ‘magic’, explains the ‘clockwork’ universe.
Free Will falls outside the ‘clockwork’. This is easy to prove via statistical modelling.
1) Imagine a machine that uses good-enough ‘pseudo’ random number generation to generate a sequence of events vanishingly unlikely to have occured in a universe of our size and age.
2) Now imagine this sequence is in a form that a person can carry out. For instance a person turning a row of 100-faced dice to match the sequence of numbers from the RNG.
The statistical likelihood of these two related events happening when the anti-science concept of ‘free will’ is ignored is essentially zero if a long enough sequence is selected. Yet every one of you here understands that you can make this happen- using your ‘free will’. This paradox has long been recognised by scientists, dating back at least four thousand years, probably much longer. Ancient thinkers had no issue accepting that science and free will could never be the same thing.
Today, despite the work of Godel and Turing, most people are taught that ‘free will’ is simply an expression of ‘complexity’. This sounds plausible to ill-educated people who mistake ‘complexity’ for ‘magic’. Religion masquerading as science, just as the ‘big bang’ (‘garden of Eden’ mythos) was introduced by people with very powerful links to organised religion. There are no microscopes on Mars, for instance, since the leaders of the most powerful organised religions still do not know how the wider public will handle the concept of ‘extra-terrestrial’ life.
There is a deep irony that the most powerful religions currently control the orthodoxy of what we may call ‘beta’ science- and that includes the falsehood that free will can arise in any system that can be defined by code running on a Turing Complete computer (such as the ‘science’ rules of our Universe). Upstart religion Scientology is mocked for being based on ‘science fiction’ ideas of ‘science’, but the major orgaised religions of our planet adopted this position 100% in the 20th Century themselves in order to survive and keep power over Humanity in an ‘age of science’. God’s act of ‘creation’ becomes the ‘big bang’, and the rules of the Universe that followed. And ‘beta’ physicists fall in line with this creationist nonsense without even realising.
For most beta physicists, some wibbly wobbly quantum random dribble ‘explains’ free will. This is actually as far from science as you can get- and is actually classic mysticism.
Read the work of alpha scientists, however, and you’ll discover these people have no issue accepting a spiritual AND scientific dimension to existence. But alphas are not the ones who tend to be answering questions on the Internet. Betas, by definition, are drones, programmed to spread the current orthodoxy, even when that orthodoxy is known to be false.
Take the well known example of the Catholic Church stating that the Sun revolved around the Earth. Ordinary people have this fact explained by a blatant LIE- namely that scientists at the time thought this true. They did not. Anymore than they ever thought the Earth flat. So why are you told that they did?
Well back then the Church felt the best psychological strategy to control the masses was to spread certain lies about the universe- the same types of lies current ad agencies use to try to persuade you to buy a given product. And to sell these lies in a convincing way the Church needed beta ‘scientists’ to believe the lies, so they would be convincing when explaining these lies to ordinary people (just as happens with ‘popular’ science outlets on the Internet today- ones that assume you’ve never heard of Godel, or learnt the implications of Turing’s theorems). Now the Church had no issue with alpha scientists knowing the truth- namely that the world is round and the earth orbits the Sun. But these Alpha scientsist, under threat of imprisonment or worse, were commanded to not discuss real science with the masses.
The same thing happens today. Ask why there are no microscopes on Mars, and beta ‘scientists’ will jump out of the woodwork to ‘explain’ why this would be a ‘bad idea’ – why it would be impossible, irrelevant, and simply provide results that would ‘confuse’.
Organised religion is more powerful than ever on Earth- every major project on our planet needs the permission of one of these religions, and that most certainly includes Russian, American and Chinese (yes China is dominated by organised religion- tho in a form unfamiliar to people in the West) space missions.
Anyway to answer the question “Do physicists really believe in true randomness (in science)?” the answer is ‘yes’ for beta scientists and ‘no’ for alpha scientists aquainted with the significance of the work of Godel and Turing. But beta scientists, with their support for creationist nonsense like the ‘big bang’ and support of NASA’s policy of ‘no microscopes on Mars’ will continue doing the work of the church in the same way that their analogues centuries ago taught the masses that the Sun orbited the Earth.
PS want to know just how awful mainstream beta science can be? Look at the near universal support of ‘eugenics’ by the ‘scientific’ community in the USA from just before the time of Darwin through until the 1970s or later. Maths can never be a ‘trend’ (cos of that little ‘inconvenience’ called ‘mathematical proof’) but for betas, as history shows, science can easily be perverted in trends. Most theoretical ‘science’ of the 20th and 21st century has been contaminated this way. Observations mistaken for fundamental mechanisms by those that do not comprehend the difference between a model and the REAL phenomenon predicted by the model.
Nicely said. I would like to comment that a subsequent state of a system can depend on all of its previous states (not just the previous one) because, otherwise, there would be an element of randomness. (I also do not believe in randomness).
I am intriqued by Zane’s proposal that religion is controlling “beta” scientists and the new, modern model is the new “creationists” model. What I don’t understand however is the belief that Free Will is separate from the “clockwork”. If you believe these things to be true, then you must believe in dualism, yes? If you believe in dualism (which makes you spiritual), then are you not religious in nature? Can you verify? I’m not accusing you of being contradictory; I realize one can be religious without supporting organize religion but you do seem to have strong feelings against creationists. Can you explain further, possibly in more layman terms?
@Zane, I like your explanation. Similar things happen with regards to biology elsewhere on the web. Many people claim that many modern scientists don’t believe in the theory of evolution. This is a most absurd claim, as all modern biology, embryology, genetics, paleontology etc. – all of them are absolutely based on evolution and thousands on universities and institutions in the world perform millions of researches all of them based on evolution.
Exactly the same way as physics is based on Newton’s laws/the laws of quantum mechanics.
Unfortunately as science becomes more and more complex, less and less educated and intelligent people can understand its particulars, and as each of them wants to have a “clear picture of how the world works” in their mind, they are prone to appeal to beta-science. This is very well exploited by religion and politicians. Betas science does not ask you to learn how DNA, RNA, eukaryotic cell etc, work.
Beta science just tells: ‘Do you see this watch lying in the field? It was designed by a human being. Similarly a cockroach or an elephant have been designed”.
Which is absolute stupidity, as the watch of course has not been ever designed! Watch has evolved for hundreds of years and its so claimed “designer” just used a previous model of watch as a base for the new one with minor changes (similar to biological evolution).
The situation in 19th century was much better. At that time nearly all educated people understood that creationism is nonsense. The only difference between now and 19th century is the vast complexity of science today which is very difficult for most (even educated) people to conceive.
@Zane, what I don’t understand in your post: how could Russians or Chinese be stopped from sending microscopes to Mars bu the world nasty religions? Indeed they have not sent ones, because Russians never landed on Mars, but Russians landed on Venus and I am wondering if hey used microscopes there.
Leo, your watch argument makes no sense: For every “evolution” of watches, it was intellectually designed from an outside source. And yes, if you trace all the way back to the beginnings of “watches”, it was obviously intelligent design. Your argument is very flawed.
Token, sorry, you don’t get the whole point. If watch could have been “created” or “designed”, why so clever a scientist as Archimedes did not do that? Why ancient Egyptians did not “intelligently design” a watch and why so clever a person as Leonardo Da Vinci or Isaac Newton did not “intelligently design” a computer or a spaceship?
Intelligent design is an illusion. Any object “created” by people that you can see around has evolved through a very long chain of trial-and-error small changes.
Every watch that you look at the shop was not created or designed from scratch. It was based on a previous model of watch which was very similar to the new one. Generations and generations of watches changed, every time some change was introduced (and a lot of times the change was actually not good but bad). The good changes were selected by the market, the bad ones discarded.
No any genius person and not a group of people and not even the whole world could have designed iPhone-7 in say 1995. This device has evolved.
No any complex system (either biological or human-made) can be created or designed at once. Only long evolution can bring complex systems to existence. Yes, watch or iPhone or Boeing 747 are created very quickly in the factory from preexisting details and drawings, similar as a human being is created from a preexisting DNA from just one human cell. But until those drawing and details for Boeing 747 have come to existence and until a human DNA and a human cell have come to existence, a very long process of evolution had been taking place.
It does not matter so much what are the small steps in this evolution: genetic mutations or trial-and-error changes by humans.
Token, if you believe that a complex thing or device can be intelligently designed from scratch, please design some devise that will exist in 2030. Say a computer or a smartphone of 2030.
Indeed why nobody intelligently designs a robot capable of say cleaning streets like humans or of talking? Such robots will probably appear in 20 years times, but not now and why is it? Because evolution is needed. A long trial-and-error process including small changes and selection.
At last, logic!
First of all, I am extremely glad to see this post, people discussing Randomness and Free Will. Secondly I am glad by the kind of explanation or opinion put by Zane.
Since many years back,I came to understand that science in simple words is the study of Cause and Effect. Everything in the universe is abiding cause and effect. Nothing is cause less. Randomness is just our inability to observe a process or phenomenon or predict the outputs because of our limitations or the limitations of our present level of technologies. However things in reality are not random or causeless. Also randomness or causeless events leads to supernatural or magic which do not exist. There’s always a reason or cause, which is again a scientific cause, behind any phenomenon no matter that cause is known or not.
Since our brains are also part of this physical world, the knowledge or memories in its neurons, the past, the moods, the circumstances, priorities etc all matters in our decisions, our so called free will is also an illusion, and not actually free will or possess ability to think randomly.
It’s great to know that future is fixed and infinite possibilities of future is just calculations. Things are flowing automatically as per set in the first event of creation.
All of this points towards the infinitely infinite creator or source.
Thank you
Swaraj Singh
Swaraj, great comment, I agree with everything except the usage of words “creator” and “creation” towards the end. I think these words should be left to religions, not science.
@Zane — flawed premise: you’re conflating science (a method of interpretation of observable phenomena) and reality (the direct experience of phenomena we observe). Science operates under the assumptions that all effect has a cause, and that rigorously identical systems evolve in the exact same way; as a consequence, reproducibility of a result is what makes it scientifically valid — which is not the same as being true, unless we can prove the underlying assumptions of science are valid in every situation.
The birth of the Universe for instance, or rather of the physical framework for the existence of matter (just in case “The Universe” is only the name for its post-Big Bang incarnation), is an indeniable case of causa sui; science can probe as far back as it can, the question “yeah, and before that?” can always be asked. In other words, the conceptual impossibility of causa sui inherent in science sends the question of the origin of our universe into an infinite regression, and since it would require an original uncaused event, it constitutes a scientific impossibility — yet here we are.
Therefore, scientific model != reality, and fundamentally so, not just because of a circumstantial lack of information. Randomness, if it exists, likewise proceeds from a causa sui, so Gödel’s theorem doesn’t apply.
And as for the guy who mentioned dualism — it’s an unnecessarily complicated view. If you believe that all our actions derive from the motion of matter in our brains, but also that an intangible element can meddle with it, then you have to explain how this element is not matter despite being able to impart momentum to matter. Dualism makes more unverifiable assumptions than physicalism or metaphysical solipsism, for the same result (the same subjective experience).
there was no beginning and there will be no end.
existence is eternal and infinite.
the clockwork will always tick.
there is no free will.
we are all players on a stage following a script re Shakespeare.
it is amazing that existence exists…i am shocked.
Pingback: Can free will exist in our deterministic universe?
@zane, It’s each to prove “Freewill” is an illusion. Just pause for a moment and think of any random world city. Really. Stop now, think of a city, then keep reading.
OK. So when you were thinking of your random city, did you consider the city of Kyoto in Japan? If not, then, I ask, did you know Kyoto was a city? How can you say that “you” picked a city randomly if you if you knew Kyoto was a city, yet you didn’t consider it? Clearly, some subconscious processes which you don’t fully understand nominated some candidates for you, and you didn’t really “pick” a random city from your vast knowledge of cities, but merely decided to stop thinking about it–and ended up with the last city presented to you.
According to the modern scientific view, there is simply no room at all for freedom of the human will. Everything that happens in our universe is either completely determined by what’s already happened in the past or else depends, in part, on random chance. Everything, including that which happens in our brains, depends on these and only on these:
A set of fixed, deterministic laws. A purely random set of accidents.
There is no room on either side for any third alternative. Whatever actions we may choose, they cannot make the slightest change in what might otherwise have been — because those rigid, natural laws already caused the states of mind that caused us to decide that way. And if that choice was in part made by chance — it still leaves nothing for us to decide.
Minsky from Society of Mind:
“Every action we perform stems from a host of processes inside our minds. We sometimes understand a few of them, but most lie far beyond our ken. But none of us enjoys the thought that what we do depends on processes we do not know; we prefer to attribute our choices to volition, will, or self-control. We like to give names to what we do not know, and instead of wondering how we work, we simply talk of being free. Perhaps it would be more honest to say, My decision was determined by internal forces I do not understand. But no one likes to feel controlled by something else.
Why don’t we like to feel compelled? Because we’re largely made of systems designed to learn to achieve their goals. But in order to achieve any long-range goals, effective difference-engines must also learn to resist whatever other processes attempt to make them change those goals. In childhood, everyone learns to recognize, dislike, and resist various forms of aggression and compulsion. Naturally we’re horrified to hear about agents that hide in our minds and influence what we decide.
In any case, both alternatives are unacceptable to self-respecting minds. No one wants to submit to laws that come to us like the whims of tyrants who are too remote for any possible appeal. And it’s equally tormenting to feel that we’re a toy to mindless chance, caprice, or probability — for though these leave our fate unfixed, we’d still not play the slightest part in choosing what shall come to be. So, though it’s futile to resist, we continue to regard both Cause and Chance as intrusions on our freedom of choice. There remains only one thing to do: we add another region to our model of our mind. We imagine a third alternative, one easier to tolerate; we imagine a thing called freedom of will, which lies beyond both kinds of constraint.”
First of all, modern science doesn’t even believe in true randomness at all, with one single exception: at the quantum level. I personally think this is fine tuning. If we can have randomness in the quantum world then why can’t we have it in the macro world? Or at the cosmological scale?
Also modern science does not preclude the discovery of other things that are fundamental. I’m very confident we are not done with that yet, if we ever will be.
Consequently, I think pure reductionism is a nonsense viewpoint. There is no evidence that randomness does NOT emerge at higher levels of physics. In fact, there is an awful lot of circumstantial evidence that it does. Sooner or later we will discover why.
infinity = randomness
For randomness to exist you need infinity, can we proof infinity?
Sure with a negative proof: infinity + 1 but negative proofs does not make it real.
We can select random numbers from nature in any finite range we choose. I do not see how infinity is at all involved … ?
I wrote about the existence of true randomness and other facts, such as consciousness, free will, the origin of the universe here: https://templeofvoid.wordpress.com/2020/05/21/existence-of-an-external-universe-to-the-physical-universe/
Does the live or dead state of car in a box become random depending on the release of a poisonous gas triggered or not by the decay of a radioactive atom? Is that the result of a quantum event but expressed at the macroscopic scale?
@zane randomness doesn’t equate to free will.
I don’t believe in randomness myself, and the idea that two “identical” experiments side-by-side are exactly the same is ridiculous. Can you confidently say that the atomic counts in the bounds of each experiment are identical? We truly believe that the angles we are measuring are -exactly- the same (down to atom-sized accuracy)? Let’s not forgot the fact that we have two experiments going on at different points in time, at different places in the universe (yes, perhaps only inches apart), and we’ve got dark matter potentially floating all around us, which we don’t yet understand and can’t see. I’m sorry, to me the idea that we have eliminated all hidden variables and have proven that cause and effect does not really exist is laughable.
Kevin-
in the assumption you are referring to the first post about John Bell’s reality
theory:
He did not disprove Einstein’s theory through eliminating every single possible hidden variable. That would be impossible. What he did was create a formula (imagine c^2 = a^2 + b^2), that by all means, should always work. and when you use normal numbers, it does- until, for some unknown reason, it simply did not. Imagine if there was a right triangle that the Pythagorean theorem simply did not apply to.
In his experiment, the equation should have worked. The angles were created with the same accuracy as in those that did work, the particles were, relatively, the same distance apart, etc.
This is very simplified, and something to be taken with a grain of salt considering I had never learned of this theory until 30 minutes ago. But I believe it gets the point across. My apologies if it was wrong, if anyone is able I would like to be corrected.
The digits of the transcendental numbers are randomly distributed.
Yes random, but repeatable and entirely predictable.
My two cents are that every dimensional frame of reference that we see evidence of seems to be contained as a series of points, or lines, or dioramas, or movies within a dimension above it. Since every such packet invariably seems to be contained within the dimension above it, it would appear to be true to suggest that each dimension is fully contained within the one “above” it. If that is the case then it would appear to suggest that all of time is “contained” within a dimension above it, which means the future is already “contained” which seems to presume information about the future (e.g., that it does and will exist, and that it will not extend beyond the bounds of the dimension containing it up to that point in time (or in, as I like to think of it, “super-time”). There also seem to exist tachyons, which, if understood to move the opposite direction of our experience of time, and if that is the case, then some future story explains the location and direction true of any given tachyon as it passes us by…a very CERTAIN future state must exist to explain its present state. There is no randomness. All states are determinable from the states that bookend them. I think both of these thoughts lead a more alpha thinking cosmologist to conclude that determinism is the only logically true explanation of the universe. It does mean that free will is a complete myth, but that doesn’t stop it from feeling very real, and navigating the universe as if it were real has served us very well as a way of making sense of our universe with limited sensory awareness of all of its dimensions.
@Kevin
I am currently writing on the subject and I found myself scrolling here, I agree with you that for randomness to exist, an input defined by its space and time has to give multiple different outputs, defined by a result from the input.
If we verify randomness by going back in time to observe an input and its output again, we simultaneously create an alternate future and therefore create randomness at that point. Matter crossing this point either continues its path to the world from which we departed or continues in the world we just formed, creating two alternate outputs for one single input.
If one merely observes the past without creating randomness, even if an input appears to only result in one output, it only suggests that randomness doesn’t exist, it does not prove it.
Impossible to verify, randomness simultaneously exists and does not exist.