Physicist: If you ever hear a physicist talking about “the edge of the universe”, what they probably mean is “the edge of the visible universe”. The oldest light (from the most distant sources) is around 15 billion years old. Through a detailed and very careful study of cosmic inflation we can estimate that those sources should now be about 45 billion light years away. So if you define the size of the visible universe as the present physical distance (in terms of the “co-moving coordinates” which are stationary with respect to the cosmic microwave background) to the farthest things we can see, then the edge of the visible universe is 45 billion light years away (give or take). However, that “edge” doesn’t mean a lot. It’s essentially a horizon, in that it only determines how far you can see.
Of course, if you wanted to know “how far can we see?” you would have asked that. The picture of the universe that most people have is of a universe enclosed in some kind of bubble. That is, the picture that most people have is of a universe that has an edge. However, there are some big problems with assuming that there’s a boundary out there.
If you decide that space suddenly ends at an edge, then you have to figure out how particles would interact with it. Obviously they can’t keep going, but bouncing off or stopping both violate conservation of momentum, and disappearing violates conservation of mass/energy. Moreover, if you say that spacetime has a definite edge at a definite place then you’re messing with relativistic equivalence (all of physics works the same in all positions and velocities). It may seem easy to just put an asterisk on relativity and say that there’s an exception where the edge of the universe is concerned, but the math isn’t nearly as forgiving.
The nicest theories today suggest that there is no boundary to the universe at all. This leads to several options:
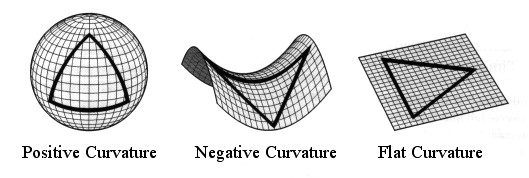
1) A negatively curved, infinite universe. This option has been ruled out by a study of the distribution of the Cosmic Microwave Background.
2) A flat (non-curved), infinite universe. The measurements so far (devotees may already know how to do these measurements) show that space is flat, or very very nearly flat. However, infinite universes make everyone nervous. An infinite universe will repeat everything in the visible universe an infinite number of times, as well as every possible tiny variation, as well as every vastly different variation. All philosophy aside, what really bothers physicists is that an infinite (roughly homogeneous) universe will contain an infinite amount of matter and energy. Also, the big bang (assuming that the Big Bang happened) would have had to happen everywhere at once. As bad as the mathematical descriptions of the Big Bang traditionally are, an infinitely large Big Bang is much worse.
3) A curved, finite universe. This is the best option. You can think of the universe as being a 3-dimensional space that is the surface of a 4-dimensional ball, in the same way that the surface of a balloon is a 2-dimensional space wrapped around a 3-dimensional ball. Of course, this immediately begs the question “what’s inside the ball?”. Well, keep in mind that what defines a space is how the things inside it relate to each other (the only thing that defines space is rulers). So even if you turned the “balloon” inside-out you’d still have the same space. Or, if you’re not a topologist, then remember that there’s nothing outside of space, and the surface of the 4-d sphere is space. Now, be warned, the “3-d surface of a 4-d ball” description isn’t entirely accurate. Right of the bat, we don’t live in 3 dimensions, we live in 3+1 dimensions (not “space” but “spacetime”), and the metric for that is a little weird. Also, when you talk about “the shape of the universe”, you probably mean “the shape of the universe right now”, and sadly there’s no way to universally agree on what “now” means in a universe with any rotating stuff in it. That being said, the “surface of a sphere” thing is still a good way to talk about the universe.
Since our best measurements show that space is very flat, if the universe has taken the 3rd “curved, finite” path (it probably has), then it must be really really big. This is for the same reason that you can easily show that a ball is curved, but may have some difficulty showing that the Earth is curved.
Also, to answer the original question: the universe doesn’t have an edge.







Yes it would look different based on different perspectives in the universe … and yes the relationship of the expanding and accelerating universe is also related to the motion of the constituents within … imagine the universe more like an ocean …
If every bit of a hologram contains all the information as every other bit, how would the view change to a hologram dweller regardless of which bit his view originated?
Thanks for your reply. I’m afraid I still don’t think I understand correctly though. If the observable universe is different on Alpha Centauri, and I actually travel there and observe the outer edge of the observable universe, I will be seeing things that were previously unobservable to me on Earth because they were travelling away from me at the speed of light. How can that be possible when I have travelled slower than light?
I realise both this observable universe, and the one on Alpha Centauri, are expanding during my travel time so the answer must have something to do with this. What confuses me is that since the two universes have different centres I don’t see how they can have the same perimeters?
@Steven Wheeler
This is a remarkably subtle question!
If you move four light years away, you’ll see events on one side of the universe four years earlier and events on the other side four years later. So, in that sense, you’re observable universe will be different. However, if you turned around to rush home to tell everyone what you saw, they’d have already seen it by the time you got home (since you’ll be traveling slower than light).
Thanks – I think it’s starting to make more sense now. You said I’d see things four years earlier if I looked away from home on my new star. Just to clarify does that means I would literally be able to see objects that my partner who stayed on Earth wouldn’t be able to see? I know there weren’t a lot of objects 4 years after the big bang but in principle if I travelled far enough would I begin to see new stars that weren’t visible before – i.e. ones that were outside of the original universe?
Or is the case that as I am moving slower than light the outer objects I can see will always be the same ones as they are travelling away from me at the speed of light?
Sorry for the very long question but to simplify it a bit what I’m trying to work out is whether it is in principle possible to see things outside of the (currently) observable universe given enough time or whether it will always be the same things but at a different stages in time.
…observing water ripples as they expand out across the lake … ripples emanate out from many different sources and places … the ripples interact with each other, peaks and troughs, … your statement involves the concept of a gods eye view in which all these ripples are being viewed from an above perspective. To then portal in to a specific place in the universe a view that perspective … is like viewing a beautiful piece of art , one that changes over time in complex fractal pattern … to zoom back out and look down on it all ripples from various sources , Rivers of Entropy flowing along the gradient and resulting in the concentration of atoms, star formation and the existence of life … zoom back in to another region and view a completely different piece Art , as before growing and scaling with time in fractal pattern. … all dice have rolled, all cards have been drawn, our perception of reality is just enough to allow survival and not so much to confuse and destroy. 10^138 coins spinning on the table , the combination of heads and tails at each moment in time creates a pattern that we perceive as reality of that moment. In fact its important to realize that when we say universe we are really refering to the observable universe … we can’t obverse Dark Matter and yet we see its effects all arounds us … then we should also not limit our thinking and distinguish between the observable universe and that which we can not detect.
Imagine the environment inside the universe is a positive charge and the ocean around the universe is negative … then perhaps Black holes are tears in the foamy fabric where the vacuum of super universal space draws out the concentrated inner atmosphere of our universe …
That was absolutely beautifully written. Excellent!
You are extremely talented. Thank you so much!
So now I’m interested in the real edge of the Universe, as it compares to the edge of the visible Universe. And in this, I would love to know the answer to two initial questions:
(a) At what time (or distance from the Big Bang) is it calculated that the outer rim of the expanding Universe reached light speed?
(b) Am I correct in assuming that all that matter beyond that point is now invisible to us on Earth?
THERE IS NO EDGE OF UNIVERSE. SUPPOSE THE MOST DISTANT OBSERVABLE STAR NAMED ‘ XYZ’ FROM EARTH IS LYING AT THE SO CALLED EDGE OF THE UNIVERSE, AND IF A PERSON LOOKS FROM A PLANET OF THAT ‘XYZ’ STAR IN OPPOSITE DIRECTION TO EARTH THEN HE WILL ALSO SEE STARS OR SPACE BILLIONS OF YEARS AWAY FROM THAT PLANET OPPOSITE TO THE EARTH . THE PERSON STANDING THERE WILL ALSO THINK THAT HE IS STANDING AT THE CENTER OF THE SPACE AND EARTH IF VISIBLE BY HIM IS LYING AT THE EDGE OF UNIVERSE.
We can only speculate on the “size” of the universe since our ability to view it is limited and because it is constantly expanding. It is a comfort to me to consider that the universe that we occupy is infinite or alternatively that it is only one of an infinite number of universes. I am satisfied with the idea that our limitation to “view” the “limits” of our universe also limits our ability to conceive of whether is has an “edge” or that it is immeasurably large and possibly getting larger. Also I am satisfied that what we can now observe is NOT the remnants of something that started a calculable number of billions of years ago from a “point” in “nothing” for some inconceivable reason and then progressed from a lot of excited, disassociated atomic particles into hydrogen atoms and on to all the other elements that we now know about. The components of the observable universe are still being formed (the Pillars of Creation) and are not merely decaying into “black holes” (whatever they are) and supernovae, etc. It is my contention that it is beyond human ability to “know” the answer to the many questions about the universe, either observable or infinite, because we don’t know enough about what constitutes the “entire” universe and whether it was formed or has always existed and is indeed infinite. Our understanding and tools with which to calculate its dimensions and construction are too inadequate.
Are black holes sucking out all the visible matter out of this universe into the super universe?
Dr. Biswajit Ghatak has it right, each place is the center of its own observable universe. If you take the perspective of someone currently on the outer edge of our observable universe, that person will be able to observe a part of the true universe that we are unable to observe and we will never observe due to the expansion of the universe. How many individual observable universes are outside of our observable universe??? How much matter would be required to explain the rate of expansion? Answering my second question should answer the first.
The good Doctor is getting a bit carried away with “observable” Universes. The fact that we can “see” parts of it matters little in the mathematics of things. The fact that the outer parts have already reached the speed of light means more and more of it disappears from our view from Earth every second. But the Universe is a big place and there’s still heaps of it left to marvel upon. As for the parts we can no longer see being the “True Universe”, I think the good doctor may need a powder and a good lie down.
I don’t think any of it ever “disappears from our view”. If it did we would no longer be able to see the earliest stars and the microwave background radiation. The “outer parts” you are referring to are the edge of the observable universe, not the entire universe. They are travelling away from us because the space in between is expanding. As far as we know the entire universe doesn’t have an edge. That’s my understanding anyway, I’m happy to be corrected. This subject always confuses me.
Ron Williams, your last two sentences are the most accurate explanation, in my opinion!!
I’ve have read many of the comments as to the question – How far is it to the end of the universe?
First of all this question has not been really thought out or the question would never have been asked! No one could know the answer period! Not you, not me or the smartest person on earth.
I do have a question and I have a proposed theory as the answer to this question.
My Question:
What was around this mass in the universe when the big bang occurred? Think hard!
This Mass had to have been surrounded by the rest of the universe (dark energy/dark matter in which it was formed). And were there more masses and galaxies out there when the big bang happened? And if so, had some of those masses ever acted like our theorized “Big Bang”, thereby creating more galaxies?
Answer:
My answer may sound too simple. The universe had no beginning and it has no end! Most of us including me can not fathom such a thing as something that has no beginning and has no end!
I do believe the big bang theory answers the question for most of us in our way of thinking-regarding our beginning. However, is that all there ever was to what most of us refer to as “The (our) Universe” as we see and know it? What if we were at the at the far end of our galaxy, would that be the end of the universe? Silly question and just as silly as asking, how far is it to the end of the universe!
Hi, this may be a dumb question but why do we say that the age of universe is 14 billion years old? I get that time is relative to where you are in space (the farthest visible star from us is 14 billion light years) but shouldn’t the age of the universe actually be distance in lightyears between the two farthest visible objects or does that only work if we assume the universe is flat?
Thanks
‘ OBSERVABLE UNIVERSE’ IS A FUNNY CLIPPING OF WORDS. BY USING A WORD ‘OBSERVABLE’ THE ENTIRE QUESTION IS AVOIDED. WHO IS OBSERVING BY WHAT METHOD AND FROM WHERE? IF ONE INTELLIGENT LIFE EXISTS AT THE EDGE OF THE UNIVERSE WHAT WILL HE SEE ON HIS SURROUNDINGS SIDES IN ALL DIRECTIONS? IF THE AGE OF UNIVERSE IS 14 BILLION YEARS THEN LIGHT FROM THAT SO CALLED EDGE OF UNIVERSE HAS ALSO TRAVELLED ON ALL DIRECTIONS. HENCE THE QUESTION OF EDGE OF UNIVERSE REMAINED UNANSWERED.
@DR BISWAJIT GHATAK
The “Observable Universe” is defined with respect to Earth. It is everything that can be observed from Earth, in every direction, as of now. Since the speed of light is finite, the observable universe is finite (light has only had a chance to travel so far).
Someone (or something) billions of light years away would observe a different part of the universe, so their “Observable Universe” would be different from ours.
@Ade
The “Age of the Universe” is defined with respect to the age of everything in it. If you had (miraculously) left a clock ticking since the earliest moments of the universe, it would read about 14 billion years today. Nothing too fancy; like our own ages, the age of the universe is the amount of time that’s passed since it stared. Distances and even topology don’t really enter into it.
Oops, if you think that the furthest matter is 14.7 billion light years away, you haven’t taken into account that space itself has expanded.
somebody refuses to do math or physics
say the big bang happened 20 billion years ago
physics claims that nothing moves faster than the speed of light
light moved away from the site of the big bang at the speed of 1 light year per year (That’s what a “light year means” (how far would light travel in a vacuum in a year)
if it moved in 1 direction for 20 billion years it would be 20 billion light years away
if it moved 180 degrees in the opposite direction along the same plane
for 20 billion years
it also would be 20 billion light years away from the sight o the big bang
so the entire universe can be no larger than 40 Billion light years across unless matter or light moved away from the big bang at faster than the speed of light
the expanding universe does not matter on the total size distance of the Universe
the speed of light = 299 792 458 m / s
a car traveling at 100 mph is going 44.704 m/s
if you turn on the cars headlights
the light from your headlights is not going 502.704 m/s
it’s still going 299 792 458 m / s
If a jet is going Mach 2 1534.54 mph it is going 686.0007616 m/s
If the jet turns on its landing lights
the light from those landing lights is not going 299 793 144 .001 m/s
it is still going 299 792 458 m / s
say the big bang happened 20 billion years ago
all light traveled away from the big bang at 299 792 458 m / s
so all light could have only traveled 20 billion light years in one direction and
20 billion light years in the exact other direction those to light points cannot be further than 40 billion light-years apart no matter how fast the universe is expanding.
btw
The final edge of the Universe will be at 1.616 times 10^35 meters and then it will collapse upon itself due to the gravitational pull of both matter, dark matter, and anti-matter
some physics guy will know why
What would the answer be to the calculation and our understanding of the result if the calculation to determine the observable edge of the Universe or the calculated mass or any other elevent calculation in physics if the mathematical rule followed was simply to do the order of the calculation differently to the current given rule ie, do the calculation following the natural order in which the expression is written or do the calculation in any order that happens to occur rather than follow BENMAS etc?
Getting back to my original question: Regardless of the speed of light emitted by the suns in the outer universe, we understand that those bodies (and all the other matter dragged along with them) at one point after the Big Bang, reached the speed of light. I would like to know at what point (distance or time) did those outer particles reach the speed of light?
Part 2 of the question is: Does Hubble’s Law have an upper limit? In other words, once the Big Bang particles reach the speed of light, do they continue to accelerate?
David
You can have a finite negatively curved 3-dimensional space. This is old news. Ask any cosmological topologist. Or any topologist for that matter. I’ll leave you with one example: The Seifert-Weber Dodecahedral Space. Fairly simple.
Yes, it was ‘old’ news from his original statement:
” 3) A curved, finite universe. This is the best option.”
What about a “flat, finite, unbounded” universe?
This sounds impossible, and indeed it is impossible for a 2D manifold like the ones you showed. However, it is possible for a 3D manifold (for example, a 3-torus), and our universe is 3D, so we should be careful when drawing conclusions from properties of 2D manifolds. Humans cannot visualize a 3-torus, but that doesn’t mean the universe cannot be like that. In fact, I thought that this was the leading theory for what the geometry of the universe is (flat, finite, unbounded).
I read today some information about GRB190114C, a massive explosion 7 billion light years away. What an amazing event to have witnessed which occurred 7 billion years ago. Unfortunately it was quoted to be the largest explosion since the “Big Bang” ! I can’t help but think that the theory on the Big Bang leaves a lot to the imagination, after all it is and will remain only a theory. The question on “how big is the universe” again can only be theorised but I personally feel that it is totally and unequivocally the nearest thing to perpetual motion/infinity that mankind will ever witness. Working on this theory tells me that any planet, star, constellation, supernova or even galaxy is in the centre of the universe no matter where it is. The amount of grains of sand on our humble little planet comes nowhere near the amount of planets/stars in the universe.