Q: What is the meaning of the term “random”? Can thinking affect the future?

2 – What is the meaning of the term “random” as it is used in mathematics/statistics? Does randomness actually exist?

---

Physicist: It does suggest that we can predict the future.  In fact, some people formulate the definition (and purpose) of science as an attempt to predict the future.

Thought alone has absolutely no impact on probability or possibility.

The predictive power of probability is fairly useless when applied to individual events.  That is to say, if someone tells you that the next time you roll a die you’ll get a 5, then they’re full of it.  How would they know that?  However, if they say that the next several times you roll a die, about 1/6 of the time you’ll get a 5, then they’ll be correct.

In that last sentence the word “about” is underlined because pretty much all of the mathematical theory behind probability is wrapped up in figuring out the details of that “about” (probability distributions, variance, etc.).

Probabilities are found by experiment.  So when you say that “each side of a die will be rolled with a probability of 1/6”, what you’re really saying is “looking at all the dice in the past, each side came up 1/6th of the time”.

“Randomness”, at least until Bell screwed everything up, is nothing more than a reflection of one’s lack of knowledge.  In practice I think it would be fair to define something as random if no one can think of a predictive model that does any better than just picking the most likely outcome.  For example, if you’re looking at coin flips and one person picks “heads” every time, and another gets a super computer, some psychics, and Mensa™ to pick sides, then they’ll both get the correct answer 50% of the time.

The interplay between perception and probability is subtle, especially where quantum mechanics is concerned.  It takes a surprising amount of study and contemplation to see where the weirdness of quantum mech enters the scene, so I’ll restrict this discussion to strictly classical (non-quantum) effects.  If you love quantum effects so much you want to marry them, then take a look at “Q: Do physicists really believe in true randomness?” and “Q: What is the connection between quantum physics and consciousness?“.  This has been a popular line of questions.

–Why thought and perception don’t do a damn thing, but seem to:  Say you lose your dog, Kolmogorov, in Madrid.  By the end of a week the dog could be almost anywhere in Spain.

Then someone spots Kolmogorov in Avila, and calls to tell you the next day.  Suddenly (by dog-spotting alone mind you) the probability distribution of Kolmogorov’s location changes dramatically.

This new probability distribution is called a “conditional distribution”.  You can tell when someone is using a conditional distribution because they’ll say things like “the probability, given that …”.  It may seem as though perceiving the dog has changed something in the universe, but keep in mind what comes first.  The dog’s location dictates where you’ll see it, not the other way around.

Another classic is the phenomenon of “hot” and “cold” tables.  You’ll find that sometimes a craps, blackjack, etc. table will suddenly be especially lucky or unlucky for a while.  It’s extremely common for people to gravitate toward tables during a winning streak, or, if things have been going well for a while, to get nervous and leave.  Both are examples of the belief that perception affects reality, or at the very least, that random things aren’t actually random.

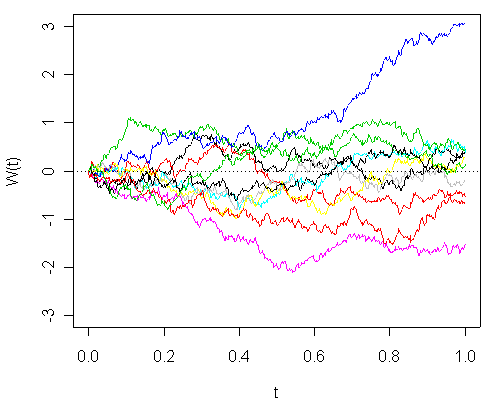
Examples of random walks, specifically the “Wiener Process”.  Sometimes it looks like there’s a pattern, but there’s not.  And yes, that’s really his name; “Norbert Wiener“.

Here’s a thought experiment (or if you have the time, actual experiment): Have a friend flip a coin.  Try to guess what it is.  How often do you expect to get it right?  Do the same thing, but this time have your friend look at the coin first before you guess.  Do your guesses get any better or worse?  Does someone “out there” with information have any influence on probability?  Hells nope.

At the end of the day, every single experiment that you can do that involves chance, and somebody having some knowledge about results, will still act exactly the same as an experiment where nobody knows anything.

For no reason, here’s a quote about Wiener: “Gifted for abstract sciences, philosophy and literature, he also had an inclination to the fine arts. These tendencies were certainly enhanced by a meditative temperament partly due to his ungainliness and myopia, which disqualified him for the usual games of physical skill popular among youngsters…”