Physicist: Back in the day, Galileo came up with the “Galilean Equivalence Principle” (GEP) which states that all the laws of physics work exactly the same, regardless of how fast you’re moving, or indeed whether or not you’re moving. (Acceleration is a different story. Acceleration screws everything up.) What Einstein did was to tenaciously hold onto the GEP, regardless of what common sense and everyone around told him. It turns out that the speed of light can be derived from a study of physical laws. But if physics is the same for everybody, then the speed of light (hereafter “C”) must be the same for everybody. The new principle, that the laws of physics are independent of velocity and that C is the same for everybody, is called the Einstein Equivalence Principle (EEP).
Moving faster makes time slow down: I’ve found that the best way to understand this is to actually do the calculation, then sit back and think about it. Now, if a relativistic argument doesn’t hinge on the invariance of C, then it isn’t relativistic. So ask yourself “What do the speed of light and time have to do with each other?”. A good way to explore the connection is a “light clock”. A light clock is a pair of mirrors, a fixed distance 
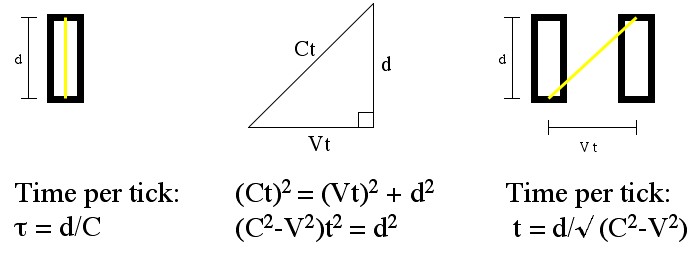
The proper time "τ" is how long it takes for the clock to tick if you're moving with it. The world time "t" is the time it takes for the clock to tick if you're moving with a relative velocity of V.
Let’s say Alice is holding a light clock, and Bob is watching her run by, while holding it, with speed V. Alice is standing still (according to Alice), and the time, 
It turns out that the really useful quantity here is the ratio: 
It may seem at first glance that the different measurements are an illusion of some kind, like things in the distance looking smaller and slower, but unfortunately that’s not the case. For Alice the light definitely travels a shorter distance, and the clock ticks faster. For Bob the light really does travel a greater distance, and the clock ticks slower. If you’re wondering why there’s no paradox, or want more details, then find yourself a book on relativity. There are plenty. Or look up Lorentz boosts. (The very short answer is that position is also important.)
The lower the slower: Less commonly known, is that the lower you are in a gravity well, the slower time passes. So someone on a mountain will age (very, very slightly) faster than someone in a valley. This falls into the realm of general relativity, and the derivation is substantially more difficult. Einstein crapped out special relativity in a few months, but it took him another 10 years to get general relativity figured out. Here’s a good way to picture why (but not quite derive how) acceleration causes nearby points to experience time differently:
Redder light at the top, bluer light at the bottom.
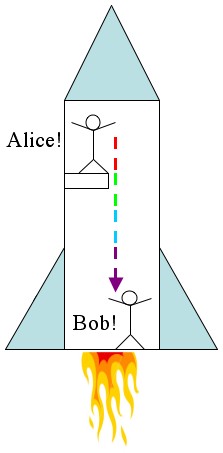
Alice and Bob (again) are sitting at opposite ends of an accelerating rocket (that is to say; the rocket is on, so they’re speeding up). Alice is sitting at the Apex (top) of the rocket and she’s shining a red light toward Bob at the Bottom of the rocket. It takes some time (not much) for the light to get from the Apex of the rocket to the Bottom. In that time Bob has had a chance to speed up a little, so by the time the light gets to him it will be a little bit blue-shifted. Again, Alice sees red light at the Apex and Bob sees blue light at the Bottom.
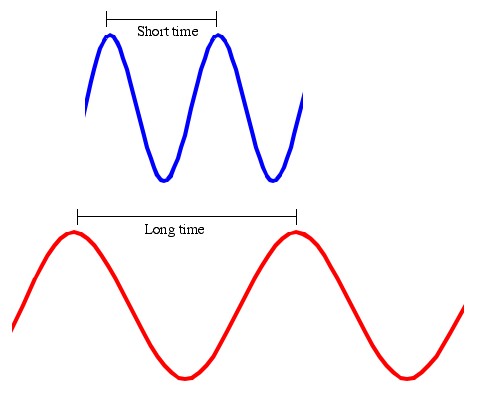
Counting the blue crests is faster than counting the red crests. However, since it's all the same light beam the number of crests has to be the same to everybody.
The time between wave crests for Bob are short, the time between wave crests for Alice are long. Say for example that the blueshift increases the frequency by a factor of two, and Alice counts 10 crests per second. Then Bob will count 20 crests per second (No new crests are being added in between the top and the bottom of the rocket). Therefore, 2 seconds of Alice’s time happens in 1 second of Bob’s time. Alice is moving through time faster.
Einstein’s insight (a way bigger jump than the EEP) was that gravitational acceleration and inertial acceleration are one and the same. So the acceleration that pushes you down in a rocket does all the same things that the acceleration due to gravity does. There’s no way to tell if the rocket is on and you’re flying through space, or if the rocket is off and you’re still on the launch pad.
It’s worth mentioning that the first time you read this it should be very difficult to understand. Relativity = mind bending.
Thank you for the answer.Though I can’t claim to have fully understood it(given my limited knowledge in physics),the idea is clearer in my head than before.It’s a very intellectually overwhelming concept.If you ponder over it for a while,there is a sort of restlessness and discomfort which begins to creep in your mind.
I couldn’t sympathize more.
Pingback: Q: According to relativity, two moving observers always see the other moving through time slower. Isn’t that a contradiction? Doesn’t one have to be faster? « Ask a Mathematician / Ask a Physicist
Pingback: Q: Why does E=MC2 ? | Ask a Mathematician / Ask a Physicist
Pingback: Q: Why does going fast increase an object’s mass? | Ask a Mathematician / Ask a Physicist
Pingback: Q: How do velocities add? If I’m riding a beam of light and I throw a ball, why doesn’t the ball go faster than light? | Ask a Mathematician / Ask a Physicist
I still have question about twin paradox.
Let’s say Alice is holding a light clock in a rocket, leaving earth, going up from the North Pole with speed of 0.9 c, while Bob watching her on earth. After a few hours, Alice comes back to earth and meets a very-very old Bob. Why Bob is getting older faster than Alice, while according to Alice, she didn’t move at all and it was Bob (and the earth) who moved down, leaving her rocket with speed of 0.9 c.
Sorry, wrong place to ask. I will ask in the twin paradox page.
No worries!
In a nutshell, the croockedness of Alice’s path means that she experiences less time. It’s not immediately obvious why, but the twin paradox page does try to cover it.
In the example you gave by using the Pythagoras theoream ( light clock) , would the result be the same if you would have taken an another human running at a normal speed ( not with speed of light ) ? In other words, what is the significance of using some object having the “fastest speed” known ( ie. photon as we know till now). Why can’t i use some bit larger speed say 100m/s etc.
It’s not the fact that light is the fastest speed that’s important, it’s that it’s always the same speed that’s important. From every point of view the speed of light is the same, whether you’re moving or not, while the “speed of runner” changes depending on how you move.
Pingback: Q: How can wormholes be used for time travel? | Ask a Mathematician / Ask a Physicist
Time dilation is so important (and REAL) that SatNavs have to make a 0.45 billionths of a second time dilation adjustment every day or else, after a week, your reported position would be 10 kilometers in error. (See my blog post http://bit.ly/wXBr9i ” A Subjective View of Time”)
Now here’s a mathematical absurdity that comes out of velocity-related time dilation! If I move my hand 0.5m away from my body at 0.5m/s then it moves into a different reality than the reast of my body because of the time dilation effect.
This of course presupposes that reality unfolds one Planck frame at a time (5.39 x 10^-44 s).
What’s more, every part of the moved arm will be in a different time zone (at the planck scale) relative to every other part. Ludicrous? Seemingly so. That suggests to me that time is either an illusion (a conscious construct) or there’s something VERY wierd about its relation to perceived reality!!
I’m still a little jogged off by this whole paradox-time-space-continium of a thing. If i could get a clearer view of what this all adds up to. And i’m starting to doubt that Flash is actually fast, what if evryone else is just super slow ? Einstein! Your a mind blower!!
We can probably lay every physics problem at Einstein’s doorstep, but the on I like best is him using a mirror to explain acceleration and C. Going from 0 to C. @ light speed would still still takes one full second. Looking in the mirror as you accelerate, the question is: Woud your image gradually fade as you approach C? And would your image disappear completely when you reached C.? So, to me time must be relative if it takes a photon traveling @ C., 13+ billion years to reach us from deep space? I hope this makes some sense.
Pingback: Q: If a photon doesn’t experience time, then how can it travel? | Ask a Mathematician / Ask a Physicist
I don’t really understand how time could slow down for someone. In that experiment with Alice pointing a laser down on Bob and that Bob was seeing blue light. Wasn’t Bob just seeing blue light because he was seeing the laser at C + the acceleration of the rocket? So he was seeing the light faster.
If I where to stop time and move at all I should be blinded or at least my vision should be blurred because there is no true image reaching my eyes. How is light = time… Also if I did stop time or slowed down time I should be dead if I moved; the friction I created would or should have burned me to ashes.
Its like seeing a plant 4 light years away. We SEE/PERCEIVE it as 4 years in the past while in reality its just as old as we are or as old as the universe.
So how does the relatively of light = time? I do not understand…..
From you article, I could make that it is the property of the clock and not ‘time’ it self which makes time slow down ? I don’t completely agree with the explanation.
we can understand almost all time dilation by examining what happens to light’s frequency under different circumstances. this works because distance and time as properties of space are quantities related to one another with the absolute constant c – the speed of light…
light (photons) has an energy associated with its frequency. this energy is a conserved constant value for each photon – a specific photon will not change its energy, it carries that energy in the electromagnetic field as a distinct quantity. because energy is proportional to frequency, and frequency multiplied by wavelength is proportional to velocity (L * f = c), photons have the convenient property that if their wavelength changes since emission, it must have been due to relativistic motion of the observer or the warping of spacetime (either one, perhaps both) on the path to the observer that altered the wavelength.
so then wavelength of light is a convenient ‘stick’ to measure changes in ‘spacetime density’ or curvature, because it directly affects the apparent color (frequency) of light passing through it (blueshift for compressed space, redshift for stretched space).
in a gravitational field, mass compacts spacetime closer together towards the center of gravity… if you were to aim a green laser on a heavy planet from one point on the surface to another, it wouldn’t change color because the gravitational field (curvature of spacetime) hasn’t changed. aiming the laser into space, it will appear redshifted, because spacetime is less compacted away from a source of gravity, therefore the wavelength of light will be stretched out (arguably the light has lost energy by escaping the gravitational field). if you did the reverse, shining the same laser onto this planet from space, since spacetime becomes more compact towards the planet, the laser will appear blueshifted (arguably light has gained energy / ‘accelerated’ by falling into the gravitational field).
how does this translate to time? quite easily. frequency is simply the inverse of period, or duration. if frequency appears to increase, but no physical quantity has changed (energy is conserved), it follows that the time in which we have made this observation of frequency, has been stretched out across more cycles.
to make this relation between time and frequency more clear… for example, if we count 5 cycles over 5 seconds, we would conclude a frequency of 1 per second. if we met a person after the fact who told us: “that wave you were looking at, it was actually 0.5 cycles per second when i sent it down to your planet”, what then? well, 0.5 cycles suggests we would need 10 seconds to observe 5 cycles… we did it in 5 seconds, and we know that the number of cycles per distance traveled didn’t change and velocity can’t change, so those 5 seconds of our experience must have been stretched out across 10 seconds from the point of view of the sender.
“… since it travels at a fixed speed (EEP y’all!) it must take more time.” – false, since the photon and Alice move in parallel (in the same time frame).
Looking at all the great names of science and the relativity of it does not mean an individual needs to understand it. People have not discovered how to bend time but the fact is that is just one source of many not created yet.
Playing god is not a great role humans play on earth for fate and promise are just primitive words not used for the seintific purpose they will be intended for. Light can be slowed down, captured and manipulated in effect of one harnessing it, it can also be reversed, the laws of physics can be defied.
All around us are resources that can be used to somewhat energise this meaning but like a jigsaw puzzle to a blind person it is supposedly impossible, Nothing can not be nothing for it is nothing, Therefore what we learn is of our own doing and the more we learn in theory our eyes and our mind open and the realism of it becomes more apparent.
Are eyes are not important what is important is our mind. The point is this, scientists are fixed on the idea that it is us that needs to travel as fast as the speed of light when, (have they ever thought), light can be manipulated around a person so that time around them can be slowed even stopped but the person is still in one place.
This is not theory or practice or equations it is fact.
I used to think like that, that time is not related to light speed. But as soon as you get it into your head that time is just a measure of events happening then it starts to click.
Look up the “light clock” example which helps a lot. where a light bounces up and down between two mirrors, taking a second to complete a full journey to and fro.
If the light clock is stationary relative to an observer, it takes a second to bounce up and down like I just said, above.
If the light clock starts moving sideways while you observe it, the light ray is then, relative to you, making diagonal movements like this \/\/\/\/\/\/.
Any GCSE student can tell you that the hypoteneuse of a triangle is longer than the adjacent or opposite…therefore the light is traveling a greater distance with each bounce.
Because we know that light travels at the same speed for any observer, irrelevant of how fast they are moving, it will always retreat away at the same speed…this is funny, but true. Even if you are travelling 1 mile an hour slower than light, the light STILL retreats at light speed away from you.
Which means, that if the light is traveling the same speed, but a greater distance, then it must be taking LONGER to do it.
This is not about LIGHT speed, this is about the property of space and time. Something is motion takes longer, relative to you to do things… it is that that is changing “time”…
Time is merely a measure of events. A year is how long the earth takes to get around the sun, for example. A day is 24 hours which is how long the earth takes to do a complete rotation.
Smaller animals experience time differently to us, they experience time as going slower, as they have faster reactions to things. So already, time has slowed down in that sense its VERY relative to the observer.
Light speed was merely the platform that enabled Einstein to deduce what was going on.
Firstly, I would just to like to say that this is a terrific forum and great read.
As a disclaimer, I have no formal scientific background but, like many, I love to ponder this stuff no matter how ill equipped (speaking for myself and no one else of course).
Just some musings. In reference to the light clock, would it be correct to assume that as the light clock approaches C, the photon’s sideways angle increases to the point that, at C, it would ultimately be moving in a straight line in the same direction and at exactly the same speed as the light clock?
As such, at speed C, wouldn’t the observer would see the photon in the middle of the light clock, with both the photon and light clock moving in the same direction and at the same velocity?
Now, until C is reached, both the observer and traveller would perceive the photon moving between the mirrors – the difference being the observer would see the photon moving in a sideways zigzag pattern moving in the direction of the flight of the ship while the traveller would still see the photon moving straight up and down within their own frame of reference.
However, when the space ship reaches C, the photon is no longer moving between the mirrors, rather, to the observer, the photon is now simply travelling in the same direction as the light clock at the same velocity of C while to the traveller, (I’m guessing) the photon would appear to be frozen in the middle of the light clock, no more ticking – would this equate to the freezing of” time” for the traveller?
Now until C is reached, I understand the traveller won’t perceive the relative slowing of the light clock due to the comparable and very real slowing down of their own physiology in every respect (including their perception of time as it relates to the “spacing” of events around and within themselves).
However, what happens at C? Until C, both the observer and traveller will at least see a photon bouncing between (ticking) between the mirrors (notwithstanding their relatively differing perceptions of time passing for each other). But at C for both the observer and traveller, the clock on the space ship will have ceased ticking. To the observer, will the traveller himself appear to “frozen” in time and what of the traveller’s own perceptions at exactly the speed of light – IF he can perceive anything at all?
And finally, I’m not sure why the photon in a light clock would endeavour to “keep up” with the forward speed of the light clock and adopt sideways movement. Intuitively, I would have thought that the photon would continue to move straight up and straight down at 90 degrees to the mirrors’ surfaces without being influenced by surrounding velocity.
With forward movement, I see the vertically oscillating photon falling to the back wall of the light clock- the back wall of the light clock then forcing the photons to begin adopting forward and partial sideways movement, the angle of that sideways movement becoming greater with increasing speed.
Anyway, just some random thoughts.
Thanks
Do you know how the human eye perceives light/time. Theoretically, could speed up the speed that your brain processed light could you have faster reflexes because you see things happening earlier? (BTW, physics is really not my strong point so please ask if something in the above comment makes absolutely no sense)
Unless there’s a black hole in close proximity, light/photons travel in a straight line. So as the the two mirrors travel sideways the light will continue to travel up and down in a straight line, not diagonally.
Which means, as the light bounces to and fro between the moving mirrors, it will bounce ever closer to the edges of these mirrors until it misses the edge and becomes absorbed by the clock casing. If it’s just two mirrors being held out in the open then the light will either hit the ground or fly off up towards the sky.
Marc – But do photons actually travel in an absolute straight line or do they only appear to travel in a straight line to observers within the same frame of reference?
As I understand it, everything is moving in the Universe so if everything is moving, the perceived path of a photon can only be measured relative to a given frame of reference. I too see an apparent contradiction in terms IF light isn’t supposed to be influenced by anything (bar the gravitational pull of a black hole) but at the same time, I have to wonder how light could ever be measured to be absolutely straight – its path always has to be measured relative to something else.
If the light clock example (photon moving diagonally) is held to be true, then in my thinking, the photon HAS to be affected by its surrounding velocity. In other words, to a distant observer, the photon will have to appear to be moving diagonally in order for that same photon to satisfy a relatively perceived straight line path for the observer travelling along with the light clock.
Relativity becomes a lot clearer ( atl least for me it did), when the Doppler effect is taken into consideration.
If the speed of light is FINITE, when two objects move apart, they will APPEAR to move more slowly than stationary objects. When two objects move towards each other, they will APPEAR to move more rapidly than stationary objects.
Consider Homer, who stays on earth, and his identical twin Ulysses, who travels back and forth to Sirius. When Ulysees starts, their clocks are synchronized. Due to all motion being relative, Homer and Ulysees should see each other slowed down at the same rate when moving apart due to the doppler shift, they should see each other speeded up by the same amount when moving towards each other. When Ulysees reaches Sirius, half the trip for him, it will take time for the light to reach Homer back on earth. Again, when Ulysees returns to earth, Homer will apper to have speeded up due to the doppler effect. For Ulysees, Homer appers to be doppler shifted slow for the 1/2 trip away, and doppler shifted fast for the return 1/2
of the trip. Since it takes TIME for the light signal from Sirius to reach earth, Homer will see Ulysses doppler shifted slow for OVER half of the time, doppler shifted FAST for LESS than half of the time. Since it was Ulysees who changed directions, Ulysees will have aged less than Homer.
Michael – When the photon is midway between the light clock’s two mirrors, it is travelling just as it would were the mirrors not there at all.
Even if the experiment were to be carried out in deep space which is expanding at 67.15 kps per megaparsec, the light clock is only a mantle clock sized and the mirrors are, say 150mm apart, so the expansion of space is of little effect.
Photons while travelling encounter a myriad of objects ranging from the subatomic to celestial bodies which of course can disturb or terminate their journey. The light clock is again very small, and the photon inside has little to disturb its path other than the mirrors.
The greater the distance you are from a star the fainter it appears to be, this to me is very good evidence that light travels in a straight line. The further the photons travel from the star, the more diluted in space they become because they are covering an ever increasing arc around the star.
Looking at the sun (with eye protection) we see its position in the sky as it was about 8.5 minutes ago, the light has travelled to us in a straight line with no respect of its frame of reference to us or the sun. We (the Earth) just so have happened to have moved into a position where we can see it in a given part of the sky. Indeed things will have moved on and the actual position of the sun in our sky is not exactly where we see it. Light leaving the sun at that moment will also travel in a straight line, and we will over the next 8.5 minutes move into a position to receive some of it.
Back to the light clock, if Tom is holding the clock to view the photon moving up and down between the mirrors, he of course is unable see anything of the photon.
Now if his Girlfriend Margaret were to stand a good distance from him and even with super powers watch the photon in the clock, she would also see nothing of the photon.
The photon is moving up and down in the clock not towards her for her to be able to see it; Tom would not be able to see it either for the same reason.
Ignoring that inconvenient problem, let’s now say Margaret with extra super powers can see the photon travelling up and down between the mirrors from 1 mile away.
While Tom stands still all is fine, both now with extra super powers see the photon happily being tennis ball between the two mirrors.
Tom gets bored and walks off to the pub with the clock and he’s that bored he decides to walk sideways though continues watching the photon as he does so.
Both Tom and Margaret would see the photon move up and down between the mirrors, not diagonally and see it come off the edge of one mirror almost as soon as Tom moves off.
The photon just as photons moving from the Sun to the Earth moves between the mirrors with no respect to its relative position to any given object around it. If the mirrors stay put, fine, it’ll just bounce off yet again. If they move off while the photon is travelling towards them, the photon does not give a flying fish, it’ll just carry on until something else interrupts its path.
If the mirrors move just a little, the photon simply strikes a different part of the mirror. Just like photons coming from the sun will strike different parts of the Earth as it continues to orbit and rotate.
What if the mirrors of the light clock were concave? That would be an interesting experiment, but its results would beside the point of this current exercise.
Marc – thanks for the response.
Superpowers are a prerequisite for a good number of thought experiments.
Of course we’re pretending that our participants can “see” the photon indirectly so that we can cut to the main bone of contention.
When can Tom ever be proven to be truly stationary? If Tom is standing still relative to ever moving Earth and Tom “sees” the photon bouncing perfectly between the two mirrors then the observed path of the photon is obviously tethered to the frame of reference. Given that condition, a distant observer moving past Tom will “see” the photon taking a diagonal path between the mirrors and still maintaining its contact at the centre of each mirror.
Now, conversely, IF the photon does move in an absolute straight line, independent of ALL else and as viewed from ALL frames, then that would mean a light clock will not work anywhere UNLESS it is fixed to an absolutely stationary location. If this condition is correct, then the perfectly fixed path of a two non interfering photons travelling horizontally and vertically between opposing mirrors could be used to confirm an absolutely fixed point in space.
As I understand it, it is deemed impossible to point to an absolutely fixed point in space because everything is moving relatively to each other and that includes the path of light (not to be confused with the speed of light which is the only observed constant across all frames).
While light will always been seen to travel in a straight path within a given frame of reference, outside that frame of reference, its observed path will be different.
A hint to why a photon might maintain it’s bounce between the moving mirrors is perhaps because the same photon isn’t being literally reflected, rather, a new and identical photon is being emitted with each bounce and the velocity of the photon’s source (the respective mirrors) actually does influence the path of each newly emitted photon.
Michael – Another prerequisite for this particular thought experiment is that we have indeed found a totally stationary position to place our light clock.
Adding one more non-interfering photon and another pair of opposing mirrors to the device for confirming a fixed point in space, making it 3 dimensional, should provide evidence that such a place may not exist.
Does the velocity of a travelling mirror really influence the path of a newly emitted photon? Travelling as if it were a solid object being booted out of let’s say, a speeding train, or even a bullet fired out of that trains window on a planet with zero atmosphere?
Even then, the force behind the bullet should pretty much nullify the comparatively tiny velocity it had prior to being fired.
Again, ignoring all the irritatingly inconvenient realities, imagine two very high speed spacecraft travelling strictly parallel and at a distance of precisely 30 light seconds from each other.
Both spacecraft are huge; in fact one full light minute in length, along the entire length of their bodywork they have light sensors which emit a pulse of light in response to detecting a direct pulse of light from any angle.
They both have an onboard computer which records precisely where on the craft a light pulse has been detected and emitted, particular attention paid at each light second of the crafts length.
Despite these huge distances the expansion of space in this frame of perspective is negligible.
Let’s also round up C to precisely 300,000kps.
Both spacecraft are travelling at precisely 10,000kps; I did say very high speed. One of the spacecraft initiates the experiment by emitting a pulse of light from precisely 30 light seconds, midway along its body.
The light clock experiment says that this pulse of light should in precisely 30 seconds, be detected at precisely midway, 30 light seconds along the other spacecraft and that a pulse of light sent in response is detected exactly where the first pulse was emitted and so on for the duration of the experiment.
I don’t think so,
The 1st pulse is emitted; it travels 90 degrees from craft 1 for 30 seconds before being detected at 31 light seconds from the front of craft 2, the sensors at 30 light seconds did not receive a direct pulse, so they do not emit light. Craft 1 receives the responding pulse at 32 light seconds from its front and so on.
So after 7 1/2 minutes craft 1 receives a 15th pulse of light on its tail pipe and emits a 16th which misses craft 2 by one light second.
A distant third spacecraft with an exceptionally high speed high resolution camera took a movie of them as they passed by. They played back the movie at various speeds, and what they saw were the 2 spacecraft passing by and the pulses of light being exchanged between them were not passing by, but to and fro between them until the last pulse missed the tail of craft 2.
Craft 1 & 2s onboard computers confirm this. It shows a pulse of light oscillating as if rebounding between two stationary objects while the two craft moved on.
Now supposing photons really are influenced by the velocity of their source and are caused to travel diagonally between the spacecraft (or mirrors). Instead of the pulse of light being detected at the exact corresponding part of the opposing craft it’s simply going to be detected further back having taken a longer path to travel between craft.
The two craft, the pulse of light are 3 independent entities travelling through space, one at a different speed.
As I said before, a travelling photon has no concept of anything its travelling towards until it’s there.
Fire a bullet at a target, the target is whisked out of way, the bullet has no concept of this, it’ll just carry on.
Later the 3 spacecraft conduct a 2nd experiment where the colossal 1 & 2 remain as stationary as space allows, and the 3rd craft belts past them several times at various speeds not too far fetched and including 10,000kps, and also at various distances.
Craft 1 & 2 exchange pulses of light midway and provided they remain lined up correctly, the pulses of light should continue to be exchanged from the same point on each craft for the duration of this exercise.
What will the crew of the 3rd craft see?
Any distance and every speed they used should reveal craft 1 & 2 exchanging a pulse of light between them. This pulse of light takes a straight and direct path with each journey.
Similar to viewing two table tennis players who had somehow perfected the art of rebounding a ping pong ball between them perfectly straight across the table whilst you belt past them at a distance on anything you wish, speeding train, jet fighter, rocket………
Clearly something is going on when objects travel at high speeds, otherwise GPS satellites would not have to be constantly adjusted. Something is definitely going on while an atomic clock is travelling in space, is it time dilation, what is it, and are there other factors? Factors we are yet to discover?
Pingback: Q: Satellites experience less time because they’re moving fast, but more time because they’re so high. Is there an orbit where the effects cancel out? Is that useful? | Ask a Mathematician / Ask a Physicist
Hi Marc
Thanks for the considerate response and your well imagined and laid out thought experiment – a virtual and absolutely massive photon clock travelling through space with solid values to be getting on with.
Here’s my take-
I’ll preface that I am accepting that the path of light inherits from the velocity of its source. As all things are in motion, I would conclude that the path of light, while always linear, does not and never does travel absolutely perpendicular to the original fixed point from which it was emitted – rather, the path of light is always relative to the motion of its source and there is no absolutely fixed reference point that can be cited to suggest otherwise .
To the thought experiment put forward:-
Travelling parallel at equal velocity (10,000 kps =1/30 C) and separated by 30 light seconds, the spacecraft are in the same frame of reference and they will observe the photon moving vertically between them, hitting the midpoint of their spacecraft each and every time. Relative to just one another, the spacecraft could just as easily consider themselves stationary. Over a 30 second period (as per the spacecraft clocks), the photon will have made 1 trip between the 2 spacecraft and the spacecraft themselves will have travelled a distance of 1 light second.
The distant observer will see and time things differently. He/she will observe the photon travelling diagonally between the spacecraft but still hitting the midpoint of the moving spacecraft each and every time. Yes, for the distant observer, the photon will have apparently taken a longer path than that calculated by the spacecraft but as per the observer’s frame, the photon’s travel will not be confined to just 30 seconds, rather, the photon will have that much longer to travel from midpoint to midpoint.
Using vectors and plugging in the values provided, the observer might calculate the distance of the diagonal path of the photon to be 30.01 seconds – yes, a longer path but the observer of course will of course also clock the time taken for photon to travel that path to be 30.01 seconds and ultimately conclude that it took the spacecraft 30.01 seconds to travel a distance of 1 light second.
The difference in timing is apparently the time dilation factor – the spacecraft experiencing a relative slowing of time as compared to the distant observer.
Don’t get me wrong – I don’t suggest that this is the be all and end all explanation. Far from it and I certainly don’t dismiss your opinion regarding the behaviour of the photon. My take is simply as much as I can grasp on the subject at this point in time but there are certainly other potential wrinkles to iron out – not the least being the factoring in of the apparent distance contraction effect.
Very interesting subject. Thanks.
hello,
First of all I think that both obervers see that the others clock runs slow because of their relative speed, if that happens then how running make you age slower than a guy that stands still ???
( I suppose we can asume that ”case 1 standing guy” is running with same speed in opposite direction and the other stands still also) *???
the same effect should happen to him, no??
I would be glad if you correct me because that tortured me a little
Thanks a lot
@George
In the twin paradox one twin genuinely does experience less time than the other, but it’s not quite as simple as “one moves and the other stands still” (post on that).
In the case described in this post, both people will see the other experiencing less time and very, very weirdly they’re both right. It tricky to understand why (post on that).
What’s bothered me the most about the light mirror thought experiment for decades is what several people have already brought up about the motion of the photon. I’d love for the Physicist to address that particular issue. It seems that the experiment requires treating the photon as a massive particle rather than a propagated wave. But using the properties of light (i.e. constant speed) requires treating light as a wave (isn’t C derived from Maxwell’s “wave” equation after all?). If you think of the light as a wave you either have to deal with the fact that the wave propagates in all directions, or if you assume you can shoot it in primarily the direction of the opposite mirror (like a laser), then you have to deal with the fact that waves propagate from the point of transmission in the direction of transmission. For omnidirectional propagation, the photons hitting the moving mirror at a future position are not the same photons that would have hit the stationary mirror. Some photons go to each location, beginning from the same point and travel different distances at C, taking different amounts of time. For directed wave propagation, the wave would continue to propagate in the direction it was transmitted. It would not have sideways movement as well because the wave was not transmitted in that direction. I think the main flaw is that C should be considered to be constant when measured relative to the direction of propagation only. If you measure the “apparent” motion of a photon (if it has any other vector besides straight ahead), then you are measuring something in addition to the propagation speed of the wave. If you could glide through placid water in a boat and tap the surface of the water as you go in a direction perpendicular to your direction of travel (like a bullet or piston striking the water very briefly), you will see the waves created propagating away from your boat perpendicularly from each point that you tapped the water. The waves would hit the shore at the point equivalent to where you tapped the water, not where your boat is once it reaches the shore.
In case my primary argument isn’t clear form my ramblings, if the two assumptions (light as massive particle vs. light as wave) lead to contradictory outcomes (time dilation vs. no time dilation, respectively), then they are not equivalent.
Hi,
I’ve been fascinated with this concepts lately.
I have a doubt: if speed is a measure of distance trough time, how can speed of light be a constant?
I mean for a stationary observer, speed of light is C, but for an observer moving at a velocity v, time moves slower, so the speed of light should be faster than for the first observer as light makes the same distance in a shorter time than observed by the 1st observer.
This I can’t understand…
If faster velocity=slower time, wouldn’t the aforementioned ‘guy on the mountain’ actually age slower? Being a greater distance from the center of the earth, he is traveling more distance per Earth rotation so is thus moving at a greater velocity than his sea level based counterpart.
I have a headache right now, thinking of all these theories and such, hehehehe….
I have a question that i have not seen addressed here on this board:
it was said that no one can ever go faster than the speed of light. if i was traveling at the speed of light in my spaceship, and turned on a flashlight inside my ship, everyone says i would see the light just as if it was shinning back on earth. there would be no difference whatsoever.
however, still traveling at the speed of light, what if i turned off the flashlight looked outside the window and saw the light that is shinning from a star? would i see photons flying next to me? since they would be going at the same speed as me, would i see them as floating in mid air?
and what if i was still traveling at the speed of light in a straight line back towards the earth, and decided to point my flashlight directly in that direction, and then turn on the light… from my flashlight to the end of my ship the light would travel at its regular speed, but as soon as it leaves my ship, would it slow down to normal, earth speed? or would people in earth get a shot of light at twice its speed?
So…as we all travel at different speeds dependent on what latitude we live at, do people that live at the equator age slower than those at a latitude of say 51.626862? If so what equations could be used to calculate one person’s rate of ageing compared to another person’s rate of ageing if you knew the two latitudes they lived at?
Pingback: Q: Since the Earth is spinning and orbiting and whatnot, are we experiencing time wrong because of time dilation? | Ask a Mathematician / Ask a Physicist
Why do we conclude that time slows down for the moving object based the shorter path of light for the moving object, whereas the observer sees a longer path of light moving forward. We can make the exact opposite conclusion by considering light going from the front of a moving train to the back. Now the guy on the train has a longer light path and the outside observer has the shorter path. So we can equally say that time goes faster for the guy on the train.
Any answers?
Can you please clarify for me:
I have been trying to understand this for quite some time and cannot wrap my head around this:
The example with the mirrors only makes sense to me if we measure time visually, and relative to light. If we measure it independent of light it does not make sense to me.
The example seems akin to saying that time slows down if we watch a movie in slow motion.
Andrew. Think of it as splitting ‘c’ into Planck scale ‘seconds’. It becomes a ridiculous amount of ‘Planck seconds’ naturally, but one tenet from Planck scale is that one ‘Planck time’ (equivalent to one ‘Planck second’ in my lose terms then) is the amount of time it takes for light to move one Planck length.
‘c’ must be ‘c’ locally defined, in all forms of ‘relative’ uniform motion for relativity to be correct, and locally measured that distance then also becomes a expression for a ultimate ‘time device’ defined by Plank scale.
If that is correct your local clock is equivalent to ‘c’.
What I don’t like is the idea of ‘time’, as defined by a observer, ticking ‘slower’ in another frame. Myself I think of it as a relation between frames of reference, making the ‘real time dilation’ measured by a twin experiment a result between frames of reference, not one frame ‘ticking slower’. If you consider yourself observing a clock on a event horizon, the reasoning of time there ‘standing still’ according to yourself (the far observer), using your local clock, will lead to all sorts of logical contradictions when we then change to some local observer being at that event horizon, at rest with and also observing this ‘clock’.
Using my first statement of ‘c’ being equivalent to the best clock you can have, splitting it to Planck scale, such an idea becomes synonymous to a presumption of ‘c’ losing its local validity at a event horizon. Meaning that time then don’t ‘tick’ locally defined and light doesn’t ‘propagate’.
Disregard me using ‘tenet’ for that proposition of Planck scales 🙂 it’s a logical definition that makes a lot of sense, so it’s no tenet (as some figment of imagination). Should have looked up my lexicon before using that word 🙂
Many of the answers above, knowledgeable though they may be, have grammar
and spelling errors, and demonstrate a frequent inability to construct coherent sentences.
Knowing scientific facts is a fine and admirable thing, to be sure, but good linguistic skills in communicating those facts is essential to comprehensive understanding.
@Language Guy
Totes. If you see errors let me know.
A very basic idea escapes me: relativity says that time slows down for someone (Alice) who is moving at relativistic speeds. But this someone is only moving relative to something else (Bob). From what I understand there is no way to “objectively” determine who is moving, Bob or Alice. So if both of them perceive each other as moving, and therefore both of them see the other one’s clock running slower, why aren’t both clocks in sync when they meet once they are stationary again? In other words, popular depiction shows Alice in a rocket coming back to Earth and seeing that Bob has aged faster; but shouldn’t it be the opposite, if Alice considers that it was Bob who was moving? Shouldn’t Bob also see that Alice has aged faster?
@LanguageGuy:
“good linguistic skills … is essential”
Taking people to task over their grammar would be more effective if done with correct grammar.
This doesn’t prove how moving faster than light slows down time… it just show how the perception of time is slowed. If I had powers and could move faster than light I would be blinded when moving faster than light since light wouldn’t be able to reach my eyes in a coherent fashion. If I saw Alice and I had powers to run faster than the speed of light I could just surf that light wave and see that the same image of her forever, she would look static since I would be moving and running equal to the speed of light, hence I would perceive her time to not be moving at all. Its like how we are looking into the past when looking at far away planets and objects, its the thought here. I thought this was a physical phenomena not a convulsed and retarded phenomena.