Physicist: If you’ve ever had to do square roots you’ve probably come up against the problem of taking the square root of a negative number. If you restrict your attention only to real numbers (0,1, -17, 
You have to remember: 1) The square root, forth root, sixth root, … of a positive number has two answers (positive and negative). 2) The square root, forth root, sixth root, … of a negative number has no answers. 3) The cube root, fifth root, seventh root, … of any number has one answer (with the same sign as the original number). These are random, frustrating, difficult-to-remember rules. Mathematicians had to deal with these all the time before the 1700’s.
Then Euler happened. He was looking at a similar problem; finding the roots of polynomials. Similar, because the question “
That’s paraphrasing, but it’s pretty accurate. He just declared that there’s a new number called “i” with the property that “i2 = -1″.
So, to actually answer: Complex numbers make it easy to take roots, and using complex numbers, all polynomials with terms up to xN have N roots.
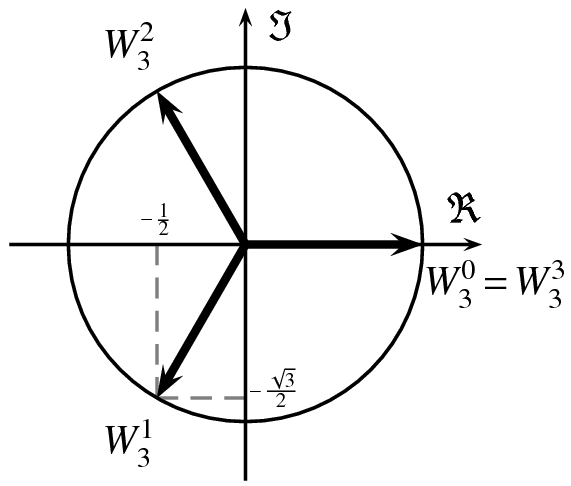
Using only real numbers, the cube root of 1 is 1, and only 1. Using complex numbers you can see that the other two roots exist, they just happen to be off of the real line. In this picture the arrow to the right is "1", and the real line is the horizontal line. The other two arrows are the other two roots. The roots of a number are always equally spaced like this.
These two properties help complex numbers “complete” the real numbers. That is to say; you don’t need to create “super complex numbers” to fix any problems with complex numbers. One of the first “problems” that people ask about is; “Sure, 
Also, if you’ve ever had to do anything with trigonometry you’ve probably come up against:
Which looks horrible, is horrible, and is horrible to deal with. Here’s the same thing (both equations) using complex numbers:
In the same vein, electrical engineers use “phasors” (phasor, not phaser) to talk about sinusoidal current (like what comes out of the wall). Again, complex numbers = easy!
If you’ve gotten stuck behind a nasty integral in calculus (and if you haven’t, ignore this), you’ll find that many of them are surprisingly hard using real numbers, but baby simple using complex numbers. For example: 
Some fields simply can’t be approached without complex numbers, particularly quantum mechanics. In QM the probability of something happening is the square of the magnitude (absolute value) of the “probability amplitude”, which is complex-valued. So, if the probability amplitude is 
where 
The moral of the story is that “complex numbers” are misnamed. While they are intimidating at first, they make things simple all over the place. Notably: trigonometry, anything with waves (electricity, light, sound), finding roots, streamlining math (often, but not always), and in quantum mechanics.
Here’s what I want to know: why do we waste so much time learning how to rationalize denominators in Algebra 2, and then never require it again in all of math and science?
Scott: Rationalizing denominators is usually a waste of time. For example, 2/sqrt(7) doesn’t look any uglier than sqrt(7)*2/7. But sometimes rationalizing the denominator is helpful. For example (sqrt(2) + 1)/(sqrt(2) – 1). If you rationalize this denominator, you get 3+2sqrt(2), which is much nicer than the expression you started off with.
Exactly what I’ve been looking for, very detailed and interesting. Was looking to do an article myself on imaginary numbers, but there’s no way I could live up to this…
Pingback: Q: Can you fix the “1/0 problem” by defining 1/0 as a new number? | Ask a Mathematician / Ask a Physicist
The theory of “black holes” was put together using complex numbers. It must therefore have the same kind of reality as the square root of negative unity.
Agree/Disagree ?
I wanna say “disagree”, but mostly because I don’t know what a “kind of reality” is.
You could just as easily say “the theory of airfoils (wings) and alternating electrical current was put together using complex numbers, so therefore they have the same kind of reality as the square root of unity”. If that statement is necessarily true, then I gotta give you the black hole thing!
Thank you for this, very informative and helpful.
I have always been bothered by the acceptance of the square root of minus one (i) as a necessity, because maths depends upon the truth that a negative times a negative is a positive. So when we allow the existence of i, even for a moment, we are also admitting to ourselves that there is some deep fault-line in our own mathematical understanding of the universe, are we not?
Now from the above I gather that we only use complex numbers to save time. That there is a long way round, all the time, every time?
Even so, either way, I do wonder whether complex numbers refer to an alternate dimension… like quantum fluctuations into and out of space, that just as you can have the square root of 1 on the positive of th x/y axes, if you flip the chart left to right, the square root of -1 makes sense…. a bit confused, I admit, but just waving at the idea.
Complex numbers are an “extension” of the real numbers by “i”. In very much the same way, negative numbers are also a string of extensions of the positive real numbers. One is no more abstract than the other. Though we do feel as though there’s something profound and mysterious about complex numbers, they’re just a bunch of symbols representing rules, quantities, and interactions, the same as everything else in mathematics.
Sorry for being so dumb (as everybody but me seems to see ‘i’ as ok), but is ‘i’ not a direct contradiction of the more foundational principle that x^2 > 0?
How it can it be a simple extension of what it undermines?
Imaginary numbers are weird to everyone.
Keep in mind that math is really about making up new rules and seeing where those rules lead, than it is about delving into the nature of the universe. It’s a heck of a lot more useful when we create math that has rules that correspond to the laws of the universe, but it’s not necessary that they have anything in common.
In this case a mathematician sat down one day and said “x2>0, so x2=-1 is can’t have a solution. But what if there were a new number such that that did solve it?”. So, it’s not that there’s some actual number that nobody noticed, it’s that “i” is a complete fabrication, that’s defined only in terms of the fact that i2=-1.
Ok, but (1) if “i” turns out to be useful in our universe, so useful that it is more than a short-cut to a long way round, but in fact is sometimes the *only* way to get to a solution, then does that not hint that there really is such a number “i” in our universe, and we just don’t know how it relates, yet? And (2), aside from that, if we mix real numbers with “i” and sometimes “i” is the only way to solve a problem which contains unknown numbers squared, how do we know which unknowns in the problem are real numbers and which square like “i”? Or, to put it another way, how can if I solve a problem containing x^2 by relying on the fact that it is positive, if x may be a member of the “i” set? Or to put it a third way, if I *have to* temporarily use “i” during the solution of a problem, i.e. cross the line between the real world and the impossible world of “i” and come back again, and the solution proves to be correct practically, have I not admitted that at the very least, there is something I do not understand? Because however theoretical it is, surely maths proofs depend on lesser proofs which in turn depend upon axioms, and if we contradict an axiom or proof in order to arrive at a new proof or statement, we cut off the theoretical branch which we are sitting on, even if the answer is correct in practice. And it is no good getting out of it by saying that there are some numbers which are exempt from our normal mathematical axioms if we at the same time depend upon those exempt numbers to behave in our normal mathematical proofs. Unless we say “it works, but we can’t say why”.
I guess I am bumbling about here. But to me it is like saying, imagine that there is such a number that when added to itself, is not 2x but 3x itself, i.e. 1z + 1z = 3z. Ok, that can be useful at times, but I suspect that no decent mathematician would accept my working some problem out which relied on that number existing, even if only temporarily during the sum.
Or perhaps – a gleam of hope here – “i” is just short-hand for “I’m too bothered to work out the way in which such-and-such mathematical description of a real world situation would express itself without involving “i”, because using “i” is quick and works.”
So there *may* be a long way round to exactly understand the real world situation, or it may involve some sort of quantum state of non-existence, but we just don’t care which?
Ultimately, every state of every mathematical equation used for the real world, should reflect some real world state, surely?
If I pause an equation reflecting some real world situation at a point where “i = {some expression}”, then {some expression} is not real – in fact, the entire equation represents a non-real state, and cannot reflect reality. The situation is impossible, and therefore we know that it is either flawed as an expression of reality, or, represents some non-real existence we do not understand.
A bit like the electron, which can be at point A at one moment, then at point B the next, and is not anywhere in the real world between those two points.
Either there must be another way to solve such an equation, or, such a non-real mathematical expression must have a non-real existence in the universe.
If I want to take a proof from A to B, and I use a falsehood on the way, or logical step which disproves the existence of A, how can I rely on my proof, unless I understand how that inbetween state is valid for A?
Sorry for the rambling….
Keep in mind, even though we’re used to “3”, there’s no such thing as a 3 in the universe at large. It’s a symbol with some properties that are useful (there’s a big difference between “useful and intuitive” and “existing”).
“i” is the exact same thing, a symbol with some properties. It’s no more or less real than any number, letter, or equation.
If you were very careful about how you define your 1+1=3 idea, then mathematicians would have no problem with what you find using that equation. In fact, there are huge branches of mathematics that look a lot like that! For example, in “mod 5 arithmetic“, the equation “3+4=2” makes perfect sense and is true.
In this particular case, if you say “X is a real number, and X^2 = -1” mathematicians would agree that there’s no solution. But, if you say “X can be a complex number, and X^2 = -1” then mathematicians would agree that it can be solved. Math isn’t ever about pulling rules out of the universe, it’s about making them up and looking at the consequences.
That helps a lot. But my sticking point is perhaps an incorrect assumption, that people mix the system of complex numbers with real numbers in the same equation, and apply the answers to real life?
I’m okay with making up numbers and playing around to see what the system producesm but if you have an equation describing some real life behaviour involving for example x^2 and then you bring “i” into that equation as well…. wait! I think I see! If I take a photograph, and fold it, and unfold it a different way to get a new insight, the beginning and the end pictures may relate to a real situation, but the inbetween folded bit does not, of course, and need not, as long as I know it. Using “i” in a real number equation is just folding the equation into a non-real, but useful, state temporarily for mathematical calculation purposes?
(I hope I’ve got it at last because I hate to waste your precious time)
(If that is the only way to fold the equation to bring it to its new state then I still think that this only path of manipulation at least hints at a non-real dimensional quantum state which our real world can get into. But I do admit of course this is equivalent to the gardener’s opinion 😀 )
Sounds like you’ve got it.
Pingback: Q: What makes natural logarithms natural? What’s so special about the number e? | Ask a Mathematician / Ask a Physicist
before explaining about square root of Negative number could you please explain about why Negative times negative number is positive
thanks with regards
Arunpradhap Natarajan
Arunpradhap
basic math
see http://mathforum.org/dr.math/faq/faq.negxneg.html
Um…………….technically for Anthony Roses equation 1z+1z=3z, isnt zero already a solution to that?(If you meant a number other than zero, sorry)
Pingback: Q: Quaternions and Octonions: what? | Ask a Mathematician / Ask a Physicist
it has alot of usage you can search on the net and see!!!!
Complex numbers are just a generalization of real numbers. The solution of x^2 = -1 is an actual number, i.
Generalizing numbers goes like this:
Natural numbers: counting objects
Whole numbers: counting objects with zero representing having no objects.
Integers: useful for accounting (money with credit and debt, assets and liabilities, balances, etc.), physics, algebra, and more.
Rational numbers: This field allows division (except by zero), which is the inverse of multiplication or the dividing up of a whole number into an number of parts of equal measure.
Real numbers: measuring continuous quantities like distance and mass, solving polynomials equations, the very existence of pi, summing infinite series, and more.
Complex numbers: This field allows all sorts of useful mathematics: evaluating certain real definite integrals, proving the fundamental theorem of algebra (useful for solving polynomial equations, of course), deriving the sin and cos of n*theta using Euler’s equation, Fourier integrals, the delta function (which is very useful in physics!), solving certain coupled differential equations, and more.
In physics the number i is quite useful:
Electrodynamics (electromagnetism), as in index of refraction, waves, simplification of certain formulas, and more.
Complex numbers are absolutely indispensable in quantum mechanics. It allows a measure of the probability amplitude (a.k.a. the wave function, often represented by the Greek letter psi) which when you take its modulus gives the probability associated with that wave function. It is in the Schrodinger equation (as mentioned in the article). It is in the momentum operator.
The quantity ict can be used as the time part of the metric in special relativity, though there’s an alternative metric. (c is the speed of light, t is time)
In each case you can make a bad argument against generalization. How can count zero objects, or assign a number to having no objects? How can you have a negative number of objects? Dividing an object in two gives two objects, another natural number. How can you have a number with an infinite number of digits? How can you have i of anything? (Rings a bell?)
The use of complex numbers allows for circular mathematics in that e^i0 = e^2*pi ; e^i*pi = e^i*3*pi. which is good for studying standing waves and modeling electrical and magnetic properties of waves which employ sine and cosine functions. Think of a complex number as a number with two properties real and imaginary. In general, we only use the real portion to describe the real world but the imaginary portion is hidden.
One of the best examples of using complex numbers I have found is when dealing with AC theory involving series and parallel circuits using resistors, inductors and capacitors. Voltages and currents can be + or – 90 degrees out of phase with that of resistors. The use of + i or – i makes things so simple.
You will need to look this up as it is 60 years since I last was involved with this theory but I do remember it as the best example I have ever found.