Physicist: Lord Kelvin (and others of his ilk) noticed that when you hold the volume of an ideal gas constant you get a nice, linear relationship between pressure and temperature.
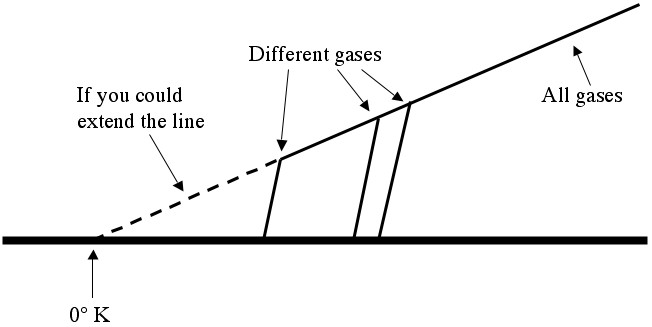
Temperature vs. Pressure. PV = nRT works for all ideal gases, independent of the particular gas in question (helium, water vapor, sulfur hexafluoride, ...). Different gases become liquids or solids (and stop exerting pressure) at different temperatures, so they drop off of the "ideal gas graph" at different points.
By the by, an ideal gas is just a gas where you can assume that the particles are bouncing off of each other much harder than they’re trying to stick together (the gas is hot enough that it’s a long way from condensing). This assumption allows you to use the “billiard ball model” of gas dynamics, which in turn leads to the ideal gas law (), which says that you should expect a nice straight line (like the one above).
Although it’s impossible to cool anything off completely, and despite the fact that all of the gases that Lord Kelvin was working with became liquids when chilled enough, it was still easy to graph temperature vs. pressure (even around room temperature) and then extend the line to find the temperature where the pressure should be zero. Kelvin figured that this would be a much more natural place for “zero” to be, and he carefully measured it (by extending the line) to be around -273.15°C, which is now 0°K (zero degrees Kelvin).
Using Kelvins instead of Celsius means that you can bust out the ideal gas law without needing to adjust anything. If you wrote the ideal gas law using Celsius instead, it would be , which is ugly.







hmmm. I never thought about that question. Nice simple answer too.
What if pressure comes below zero?
Pressure is caused by molecules bouncing off of each other. You can make the pressure higher by bouncing them harder (raise the temperature), or you can make the pressure higher by adding more gas, so there are more molecules to do the bouncing.
When you remove the gas the pressure drops. If you remove all of the gas there’s nothing left to bounce, and the pressure is zero. Since there’s nothing left to remove, the pressure can’t drop any further.
Similarly, if you drop the temperature the molecules so down. If you (could) drop the temperature to zero, the molecules would stop moving altogether, and the pressure would be zero again. Since you can’t get any slower than stopped, the pressure can’t be dropped any lower.
Long story short: pressure has to be zero or higher.
>and he carefully measured it (by extending the line) to be around -273.15°C, which is now 0°K (zero degrees Kelvin).<
I do apologize for commenting this, but it always annoys me when units are not correctly used: The Kelvin scale has no degrees !
(For the rest: great site , beautiful questions and great answers. Keep it up!)
thanks for your valuable clarifications………….they are simply great.
Given that all energy exists in discrete units (quantum physics) and that gravity drops exponentially with distance, what is the absolute maximum distance of gravity? (beyond this range even the most massive black hole will have no gravity field)
Astronomers use red shift as proof of galactic expansion. Is it possible (instead) that light just loses energy as it travels through space, and that causes the red shift?
where can i find the actual source that details more about his experiment?
Gravity decreases at a rate proportional to 1/R^2, where R is the distance between two objects. Technically, no matter how far away two objects get, they never ceases to have a gravitational effect on each other.
http://www.tested.com/science/physics/452657-science-beats-absolute-zero-negative-temperatures/
@mike – regarding light redshifting on its own – not proven so but to briefly restate what i have commented on other articles here already: light is only assumed to not redshift on its own because we don’t know how it could change frequency or wavelength without gaining or losing energy, which would alter its momentum, which would mean light does not travel at constant speed (proven to be false; it travels at c for all inertial observers). so we assume the energy, frequency of a photon is set and any redshift must be due to relativistic (ie doppler) effects. there are theories on how it could still appear to have varying frequency / wavelength while conserving energy and the speed of light but they are not presently accepted. last point – same guy who came up with dark matter, first proposed this very idea.
@physicist
re @avi’s link (beat me to it) – what would gas pressure be like for negative absolute temperature? i could be wrong but your definition of pressure may not apply correctly to the statistics of negative K particles. in any case curious how pressure applies (and what it means) to such conditions.
In repsonce to Mike Dickinson’s first comment about distance reducing the force of gravity(which is included above)
____________________________________________________________
Given that all energy exists in discrete units (quantum physics) and that gravity drops exponentially with distance, what is the absolute maximum distance of gravity? (beyond this range even the most massive black hole will have no gravity field)
____________________________________________________________
Technically, never, because no matter how much you divide a number, it will never hit zero. However, if you get far enough, the gravitational pull will be so insignificant that you might as well leave it out of you considerations.
That’s why 0 Kelvin is not a temperature but an absence of temperature. Anyway, from what I was teached.
We don’t use “degree” for Kelvin.