Physicist: Nothing really.
Complex numbers are very useful for streamlining a lot of different types of math, generalizing ideas, and “closing” the real numbers. In quantum theory you’ll find that on the most fundamental level the universe seems to prefer complex numbers to real numbers.
But you can’t use them to count or measure stuff for crap, so most people can live long happy lives without being particularly bothered by complex numbers. If you can call that living.
Mathematician: There are many ways to view complex numbers, but one of the most intuitive is to think of them as representing points in the plane. Doing so will allow us to interpret basic arithmetic operations like addition and multiplication as performing geometric manipulations.
How does this work? Well, every complex number z can be written as where x and y are real numbers, and i is the square root of -1. We can then think of z as a point on the (x,y) plane with x being the position along the horizontal (i.e. real) axis, and y the position along the vertical (i.e. imaginary) axis. To understand the operation of adding and multiplying complex numbers though, we need to think about them slightly differently.
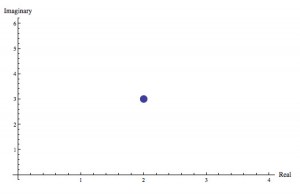
The complex number 2+3i represented as a point in the complex plane. Have you ever seen a more boring image in your life?
If we choose, we can treat complex numbers as vectors rather than points. That means that now represents not the point (x,y) but rather, the directed line segment which extends from (0,0) in the complex plane to (x,y) in the complex plane (unless otherwise stated we will assume here that our vectors are emanating from the origin (0,0)). You can think of a vector as simply representing a magnitude (or length) and a direction. The line segment extending from (1,2) to (-4,5) is the same as the one extending from (-4,5) to (1,2), but the vectors represented would be different because they would be pointing in opposite directions. Vectors are often drawn as arrows.
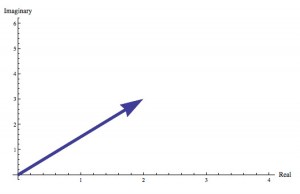
The complex number 2+3i represented as a vector in the complex plane. Compared to our last image, this is a hoot.
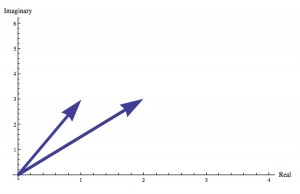
Once we have the vector notion of a complex number, we can think about adding complex numbers as adding vectors. For example, if we have
and
then
.
Hence, is the vector in the complex plane that extends from (0,0) to
. Note that
is the point we get to if we piggy back vectors z1 and z2 and then follow them both. By this I mean that we translate (i.e. move without rotating or stretching) z2 so that its beginning is at the end of z1, and then we follow the path consisting of the two vectors until we get to the (new) end of z2. However, since
, we can also piggy back z1 at the end of z2 to get the same result. A slightly different view is achieved if we think of our first number
as being a vector, and our second number
as being a point. In this case,
simply corresponds to moving the point
by the distance and direction represented by the vector
.
Alright, so addition of complex numbers can be thought of as adding vectors in the complex plane (or moving a point by the distance and direction stored in a vector), but what the heck does multiplication do? Well, to understand multiplication we need yet another geometric way of thinking about complex numbers.
First though, we make a quick (and relevant) aside. For any complex number z, we have by definition that the absolute value of z satisfies
which is precisely the formula for the distance between the point (0,0) and the point (x,y). Hence, measures the length of the vector that z represents. Now, according to Euler’s formula, we have that for any real number
.
hence is a complex number since it is the sum of a real and imaginary number. In particular, we have
That means that any complex number representable in this form must have a distance of 1 from the origin. In other words, such numbers represent points on the unit circle, or equivalently, vectors of length 1 extending from the origin. As it turns out, all vectors in the complex plane with length 1 can be represented in this form. But what angle does each of these vectors point at? Well, we compute the angle of the line segment (0,0) to (x,y) with respect to the horizontal axis using . In our case though, since
and
this gives:
.
Hence, the complex number represents a vector of length 1 pointed at angle
. Similarly, for any non-negative number r, we have that the complex number
represents a vector of length r pointed at angle . This provides a new way of thinking about a complex number: as a vector specified by its length and angle. What happens when we multiply two such numbers
and
together? Well, we have
.
Hence, is a new complex number representing a vector of length
pointed at angle
. Therefore, we can think of the action of
multiplying
as causing the vector
to stretch by a factor of
and rotate by an angle
.
Hence, to recap, we can view complex numbers geometrically as representing points or vectors in the complex plane. If we do this, then adding complex numbers corresponds to adding together vectors, or equivalently, moving the point that the second complex number represents along the vector that the first complex number represents. On the other hand, we can think of multiplication of complex numbers as corresponding to scaling and rotating the second complex number in the multiplication by the length and angle inherent in the first complex number. Finally, we note that taking the absolute value of a complex number corresponds to measuring the length of the corresponding vector. Therefore, one way to view complex numbers is as a means for converting geometric operations (translation, rotation, scaling) into algebraic operations (adding, multiplication) and back again. As you might imagine, this can be extremely useful!







In quantum theory you’ll find that on the most fundamental level the universe seems to prefer complex numbers to real numbers.
What does that mean? does that mean there are “things” at the fundamental level whose amount is measured with complex numbers?
Normally when you want to figure out the probability of something happening you add up the probabilities of every possible way it can happen. If you want to find the probability of something in quantum physics, you add up the “probability amplitudes” of every possible way that thing can happen, then take the magnitude (a generalized absolute value) and square it.
The probability amplitude is complex valued.
Hey Mathematician, great explanation!
What is the role of multiplying two vectors in order to link and match search words? How would you do it, and what is the benefit? I am already aware of two multiplication methods. One is the dot product and the other uses cross product. The description of the method was not clear on what specific calculations were performed.
e^(in)∫t*e^(in) spells einstein.
Complex numbers are used to describe dependencies on more than one axis.
If you have the x & y axis, then complex notation would be x+jy. Any line, has at least two axis (planar). A 3 dimensional curve, can be described by a rotating complex number. The axis representations are (x,y,z)=3D linear, (x,y,phi)=3D cylindrical,
(x,theta,phi)=3D polar.
The lot of the universe, is fractally composed of 3D polar coordinated (and a not so coordinated substance called, lolz, intelligence).
First they tell me that you can’t divide by zero, but if that were true there would be no such thing as a vertical line. Then they tell me that you can’t take even roots of negative numbers, but there’s a whole branch of mathematics based on that. Is there anything that actually is mathematically invalid?
The existence of verticle lines does not actually depend on dividing by 0. It is actually the slope of that line that is undefined because you cannot divide by 0. The equation of any verticle line however’ is simply x=c where c is a constant. The equation is perfectly valid and holds. But the slope, or the rate at which the line is moving up, relative to the rate at which it is moving over is undefined because our convention for slope is rise/run. However, if ancient mathematicians decided to set the ratio up run/rise, it would be horizontal lines that have a slope that is undefined, but neither of these scenarios would make the equation of either a verticle or horizontal line invalid. It may also be worth pointing out that the existence of a verticle line does not prove nor even suggest that you can divide by zero, in fact you can’t. And its not that it is impossible either, although many would tell you that it is. Its just that as of yet, we do not know how to do it, nor how to even interpret any number a/0. So we say that it is undefined which is exactly as it states, all that means is that we as people, have not yet defined, or have not yet been able to define it.
Plz Tell Me How we Represent Complex Number In Plane
Are more superficial and explaination that is designed to reside in your gut, but wont make you able to to solve anything comes here: (this is greatly simplified)
Complex numbers are good for explaining everything that oscillates.
This is due to the way the complex exponential function works.
Many real life systems oscillate. Imagine a stone hanging from a spring. (or a car resting on its suspension).
If you poke the stone it will start to oscillate up and down with some frequency but it will eventually die out. This system can be characterized by two complex numbers (ideally) that are closely related. (in fact they are the solutions to a second order polynomium).
If for example the system was suspended under water, it would probably not oscillate when poked but rather slowly return to its initial point. Because there is no oscillation the two complex numbers become real numbers instead.
The larger the imaginary part of the number, the higher the frequency, and the lower the real part the faster the system comes to rest. In fact if the real part is zero the stone will just oscillate forever, but for this system the number will be negative which causes decay of the motion. (positive will cause the system to have larger and larger oscillations and eventually obliterate earth and everyting else – ideally that is (or?).
So the short answer is that complex numbers are good for describing oscillating systems.
BR
May anyone please explain me what does a complex function like w= f(z)=u(x,y)+iv(x,y) represent in Physically sence. it also involves two independent variables and a dependent variable. How is it different from a 3d.function representing a solid. I shall be grateful for your explanation whatsoever.
@Anonymous
Math and physics don’t have a one-to-one correspondence. The same math can be used in many different contexts (and generally is), so there’s no one answer for you.
However! A really good example of complex functions in physics is in two-dimensional fluid flows (which also describes three dimensional fluid flows that don’t have a lot of movement in some particular direction). The Cauchy–Riemann equations for u(x,y) and v(x,y) describe conservation of mass and non-rotation in fluids, paving the way for the beautiful connection between fluids and conformal maps.
This write up describes briefly how to use complex functions to derive lift on a wing.
Suppose I get a solution to a differential equation in the form of a complex number (x+iy = r.e^(itheta))
Is this solution valid ? If so, Why ? What is the numerical value x = r cos(theta) or sqrt(x^2 + y^2) ?
I would think that it is not valid because the solution is imaginary.
@Sreedhar
It depends on the situation. If you’re describing something like lengths, then only real numbers make sense. If you’re describing the time since a process started, then only positive numbers make sense. Generally speaking, you have to consider carefully what you’re talking about. If an answer doesn’t make sense, then it’s not an answer (complex or not).
Pingback: Why are complex numbers necessary? - LawuNews