Physicist: Bell’s theorem, and its philosophical fallout, is one of the most profound discoveries since relativity.
Bell’s theorem states (among other things) that the universe is fundamentally unpredictable, and that quantum mechanical things (for example: everything) are not actually in one state. If a box could contain either a blue marble or a red marble, then when you open it you’ll see either one or the other. In “reality” it was one color or the other before you open the box. In QM, it can be both before you open the box (it’s actually still both afterwards, but moving on…).
Einstein (and most other physicists of the time) believed that if you knew everything about a system of particles (no matter how big) that you could theoretically predict what that system will be doing in the future, perfectly. Homeboy thought that the only reason that the movement of air molecules seems to be random, is that we can’t perfectly measure that exact position and velocity of every single one. So he thought that every particle truly is in some particular state, but that we merely don’t know for sure what that state is (the marble in the box has only one color, but we don’t know what it is).
The idea that randomness and unpredictability are caused by unknown (or unknowable) things is called “hidden variable theory” (The ‘Stein believed in this). For example; 2, 2, 3, 6, 0, 6, 7, 9, 7, 7, 4, 9, 9, … is not random, but seems random. It would be really hard to predict the next term (7) if you don’t know the hidden variable. (BTW, the “hidden variable” is: this is the decimal expansion of 
Bell’s theorem essentially boils down to a proof that the result of an experiment doesn’t exist until the measurement is made (so it can’t be predicted). Hidden variable theory presupposes that the particles involved are in definite states, which means that the result of a measurement already exists before the measurement is made. For example: before you open a gift what you’ll see is already set in stone. The gift is a set thing before you open the box. This is not the case for most quantum mechanical systems.
Here’s one of the experiments that demonstrates Bell’s theorem, and two ways to look at it.
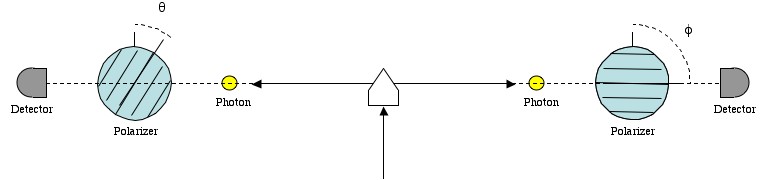
An entangled pair of photons is created and fired in opposite directions. En route the polarizers are randomly oriented, then the detectors measure whether or not the photons pass through. This is done hundreds of thousands of times to measure the relationship between 1) the difference in angles between the polarizers and 2) the probability of measuring the same result.
The experiment: Step 1: Create a pair of entangled photons and fire them in opposite directions. Entangled particles always yield the same result when they are subjected to the same measurement, and are likely to yield the same result for similar measurements.
Step 2: Randomly orient the polarizers, after the entangled pair is created, but before either is detected (this is hard to time, and is really fast). This is done so that the photons “don’t know what to expect” and “can’t compare notes”. Information about polarizer A would have to travel faster than the speed of light to get to photon B before photon B hits it’s own polarizer. So, without faster than light effects (which don’t exist for many, really good reasons) the photons are each acting independently. The orientation is random so that the photons can’t “plan ahead”.
Step 3: Measure the polarization. If the detector “clicks” then the photon made it through the polarizer, and therefore has the same polarization. If the detector doesn’t click, then the photon had the opposite polarization and was stopped.
The probability of the measurements being the same (for an entangled pair) is 
The possible polarizations for polarizer A (red) and polarizer B (blue).
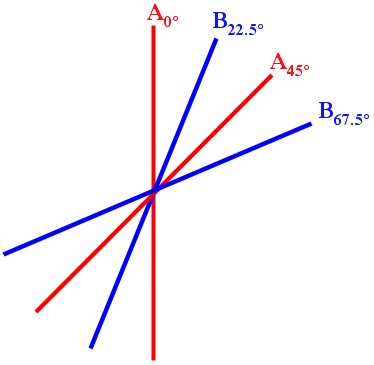
Algebraic approach: Restricting the possible angles of the polarizers to 0° and 45° for A, and 22.5° and 67.5° for B, run the experiment. Here’s what’s about to happen:
1) If you could predict the outcome of each version of the experiment, then you could find a definite value of L (see below).
2) For strictly (unarguable) mathematical reasons L = ±2.
3) Experimentally we find that the average value of L is 2√2.
4) But this is a contradiction, so we cannot actually make useful predictions.
Now it’s happening:
If polarizer A is at 0° and the detector clicks then you’d say “A0 = 1″, and if the detector doesn’t click then “A0 = -1″. Similarly, you can define B67.5, A45, and B22.5. Just for the hell of it, take a look at: L = A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5 = (A0 + A45)B22.5 + (A45 – A0)B67.5
L = (A0 + A45)B22.5 + (A45 – A0)B67.5 = ±2, since either (A0 + A45) = ±2 and (A45 – A0) = 0, or (A0 + A45) = 0 and (A45 – A0) = ±2. So if you could fill out each of these values (A0, A45, B22.5, B67.5), then L = A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5 = ±2 which, notably, is less than or equal to 2.
However, you can’t make all of these measurements simultaneously, so you can’t actually get A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5 for each run of the experiment. The best you can do is find one of these four terms each time you run the experiment. For example, if the polarizer A was randomly set to 45° and the detector clicked, and polarizer B was randomly set to 22.5° and the detector didn’t click, then you just found out that A45B22.5 = (1)(-1) = -1 for that run.
You can however find the expectation value by running the experiment over and over and keeping track of the results and polarizer orientation.
E[A0B22.5] + E[A45B22.5] + E[A45B67.5] – E[A0B67.5] = E[A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5] ≤E[|A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5|] = E[2] = 2.
So E[A0B22.5] + E[A45B22.5] + E[A45B67.5] – E[A0B67.5] ≤ 2. This is one version of “Bell’s Inequality”, and it holds if each term (A0, A45, B22.5, B67.5) has a value.
Using the fact that the chance of getting the same result is
![E[A_0B_{22.5}]=P(same)-P(different)=\cos^2{(22.5)}-(1-\cos^2{(22.5)})=\frac{1}{\sqrt{2}}](https://s0.wp.com/latex.php?latex=E%5BA_0B_%7B22.5%7D%5D%3DP%28same%29-P%28different%29%3D%5Ccos%5E2%7B%2822.5%29%7D-%281-%5Ccos%5E2%7B%2822.5%29%7D%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%7D%7D&bg=ffffff&fg=000000&s=0 "E[A_0B_{22.5}]=P(same)-P(different)=\cos^2{(22.5)}-(1-\cos^2{(22.5)})=\frac{1}{\sqrt{2}}")
You’ll find that:
![E[A_0B_{22.5}]+E[A_{45}B_{22.5}]+E[A_{45}B_{67.5}]-E[A_0B_{67.5}]=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{-1}{\sqrt{2}}=2\sqrt{2}](https://s0.wp.com/latex.php?latex=E%5BA_0B_%7B22.5%7D%5D%2BE%5BA_%7B45%7DB_%7B22.5%7D%5D%2BE%5BA_%7B45%7DB_%7B67.5%7D%5D-E%5BA_0B_%7B67.5%7D%5D%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%7D%7D%2B%5Cfrac%7B1%7D%7B%5Csqrt%7B2%7D%7D%2B%5Cfrac%7B1%7D%7B%5Csqrt%7B2%7D%7D-%5Cfrac%7B-1%7D%7B%5Csqrt%7B2%7D%7D%3D2%5Csqrt%7B2%7D&bg=ffffff&fg=000000&s=0 "E[A_0B_{22.5}]+E[A_{45}B_{22.5}]+E[A_{45}B_{67.5}]-E[A_0B_{67.5}]=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{-1}{\sqrt{2}}=2\sqrt{2}")
Holy crap! 
God plays dice with the universe.
Maybe, if you’re clever and have ready access to a time machine, you could go back and do all the measurements you didn’t make the first time. Then all the results would have to exist! They’d just have to!
Me and my time machine vs. quantum mechanics: If the results exist, but you just didn’t happen to do all the measurements, why not get a time machine? Then you could do one measurement, go back, do a different measurement, go back, do a different measurement, … Then every possible result would be known.
However, once again that correlation probability (
So, for example, if the photon goes through at 50°, and then you go back in time, change the polarizer to 51°, and repeat the experiment, then there’s a 99.97% chance (cos2(1°) = 0.9997) that the photon will go through again.
One result from probability says that 
So, if you go back and forth in time to measure whether or not the photon goes through at 1° increments, then there’s a 97% chance that by the time you get to 90° you’ll be getting the same result you did at 0°. However, in reality 
But this is a contradiction. So the results of each measurement (A0, A1, A2, …, A90) can’t all exist.
If I had to guess, every time you go back in time the experiment is completely reset, and the experiment becomes completely random again. The reason (such as it is) is below this unsettling picture.
Wait. Wait… Why?
But why?!: It turns out that the reason that the results of a quantum event can’t be predicted, is that every possible result of that event plays out. So if you ask “will I see the photon go through the polarizer?” the answer is “yes, some versions of you will see the photon go through” and an equally valid answer is “no, some versions of you will not”.
If different versions of you will see every possible result, then the result can’t be predicted, and doesn’t really exist one way or the other until after the measurement is done. At that time the different versions of you will disagree on the result. But don’t worry too much. You’ll never meet you’re parallel-universe twins.
Do you have any opinion on Joy Christian’s work: Disproof of Bell’s Theorem by Clifford Algebra Valued Local Variables (http://lanl.arxiv.org/pdf/quant-ph/0703179)?
Pingback: Quantum mech, choices, and time travel too! « Ask a Mathematician / Ask a Physicist
Pingback: Q: Copenhagen or Many Worlds? « Ask a Mathematician / Ask a Physicist
But does the polarizer constitute a measurement? Because it is not as if the photon isn’t interacting with the crystal lattice of the polarizer or the metal and dielectric of a wire grid polarizer.
There’s a subtle, but important, difference between “interaction” and “measurement”. For example, sugar water affects the right and left circular polarizations of light slightly differently, with the effect that rotates the linear polarization. So the sugar water interacts with the photons, but no measurement is ever made. The amount of knowledge and the lack of knowledge you have about the photon before and after passing through the sugar water stays the same.
In a polarizer, the light certainly needs to pass through it, and so will interact with the constituent matter (air, plastic, whatever). However, the “polarizerness”: that light with one polarization is blocked, while light with the opposite polarization passes through, is absolutely a measurement. Whether or not light passes through tells you something about the photon’s polarization that you may not have known before.
Pingback: Q: If you zoom in far enough, what do particles look like? « Ask a Mathematician / Ask a Physicist
This is so difficult to accept… From what I understand: it is not because we don’t know the “hidden variable” it is because it doesn’t exist at all!
Is that so?
So a particle doesn’t have momentum — if it has a position.
This just brings up more questions, like: Why does this not apply to bigger things, like humans? How big does a thing have to be before the theorem is true?
It always has both, just not a definite value of either. The uncertainty principle applies on all scales, but you’d never notice it on a large scale. The errors implied by the uncertainty principle are really, really, crazy small. But they’re not zero.
Ah ok, I see.
Pingback: Q: According to the Many Worlds Interpretation, every event creates new universes. Where does the energy and matter for the new universes come from? | Ask a Mathematician / Ask a Physicist
yeah i’m sure i will never meet my are parallel-universe twins either.
Pingback: Q: If quantum mechanics says everything is random, then how can it also be the most accurate theory ever? | Ask a Mathematician / Ask a Physicist
“The errors implied by the uncertainty principle are really, really, crazy small. But they’re not zero.”
I just posted in another article of yours referring to basically the same thing. I’m not a physicist, which may be obvious, but as an outsider it is hard not to think that a lot of modern physics is what I would call “mistaking the map for the road.”
The Uncertainty Principle, for instance: just because we do not possess tools that can measure location and velocity perfectly at the same time is not proof that the particle actually sort-of-exists in a probability cloud. A probability cloud may be a great tool for describing the results we get when observing an electron, but that should not be taken to assume that it represents the ultimate reality of what is going on. Just because we cannot prove or know exactly where it is and at what velocity is not proof that it doesn’t have a true location and velocity.
The idea that light is both a particle and a wave (forgive me if this is no longer a relevant concern, but I know that it was at one time)…seriously, has it never occurred to anyone that it is neither and that particles and waves are artifacts of human perception, even (or perhaps especially) when that perception is filtered through millions of dollars of instruments?
This is not some magical case of reality being simultaneously in two contradictory states at one time–this is the result of our failure to fully grasp the ultimate reality, which is quite probably not self-contradictory if we could see it for what it is.
My guess it that the “hidden variables theory” is right on the money, and furthermore that its basic concept is more broadly applicable than was originally intended.
I have the feeling that a whole host of the things that have been mathematically “proven” in the last few decades will someday be seen to have no relation to the reality they are attempting to model.
What Bell’s Theorem shows (in the article above) is that “local hidden variables” are inconsistent with experiment (impossible). This means that either 1) thing conspire with each other in a very mysterious, faster-than-light way (this is non-local), or 2) things are not in a definite state (no hidden variables).
There’s a lot of very direct, straightforward experimental evidence for many-stateness (for example, in fact there’s even a post that talks about one example!), and also a lot of both theoretical and experimental evidence showing that faster than light stuff is impossible.
Physicists are pretty good about tying theory to physical experiment, and at the end of the day physical evidence always wins (even if it messes everything up, or makes you look bad). So, while quantum theory may be a pretty set of theories and equations, if they weren’t all thoroughly backed up by experiment after experiment, they would have been abandoned.
With regard to the uncertainty principle, it is a mathematically derived statement, but it’s based on very sound physical principles, and it’s stood the test of time (and also tests). It’s just one manifestation of “many-statedness”.
It’s taken me a very long time to wrap my head around Bell’s Inequality, but I finally have, thanks to some simplified math I found off in some corner of the internet. (My math is… bad. I can’t math.). My request is: can you write an article that explains it in a way that could be understood with just a good grasp of algebra? It’s such an important cornerstone of physics, and it goes ignored/misunderstood mostly because of that, I think, when really, it’s a very simple thing.
Thanks, and I love the site.
I think this article is misleading.
After decades of trying, no experiment has been able to rule out Einstein’s local realism or establish QM’s predicted, non-local entanglement as an actual phenomenon.
Google “loopholes in Bell test experiments” and you will see. All experiments to date suffer from problems, generally either insufficient detection rates or cross-talk problems. The Bell’s Theorem inequalities, correctly accounting for real experiments, are not violated.
The best Bell’s Theorem experiment to date – I think it’s Ansmann’s – seems almost close to establishing “spooky action at a distance” but is compatible with and actually accurate enough to be in support of local realism.
Pingback: Q: Why is Schrodinger’s cat both dead and alive? Is this not a paradox? | Ask a Mathematician / Ask a Physicist
My god, you really did try hard to make this article completely incomprehensible. Well done.
I understand Bell’s Inequalilty and the modified inequality that takes account of detection inefficiencies. Surely potential detection inefficiencies affect the prediction of QM. However, I have never seem a modified QM prediction that also takes account of detection inefficiencies. Can you direct me to any such accounts?
They show up a lot in the experimental papers that actually verify the Bell inequalities. Errors are a pretty standard problem (they’re the problem), and dealing with them is such old hat that it generally gets glossed over.
Paul Kwiat and Anton Zeilinger have both done a number of (fairly dense) papers on this sort of thing.
Pingback: Morally speaking, are Atheists and Muslims immoral? - Page 15 - Christian Forums
It’s already been mentioned, but it’s worth restating, that a violation of Bell’s Inequality does not disprove the possibility of hidden variables. Bell himself was a fan of Bohm’s theory, which is a hidden variables theory.
The theorem states that there is a difference between the predictions of theories based on local hidden variables and those of QM. The key word here is ‘local’. Violations of Bell’s Inequality suggest that at least one of the assumptions he made in proving his result (which he took from the Einstein-Podolsky-Rosen argument) must be false: either nature is non-local or hidden variables do not exist (or both).
But in the EPR argument, the orthodox interpretation of QM (non-real, no hidden variables) was shown to require non-locality to account for QM’s predicted correlations between measurements separated by a sufficient distance. Einstein simply would not countenance the idea that nature could be non-local, that there was no ‘spooky action at a distance’, and so he concluded that QM was incomplete because it had no other way of accounting for its predicted correlations.
So even if Bell’s Theorm is taken (wrongly) as demonstrating that there are no hidden variables (non-real), the EPR argument is that nature must still be non-local. So, what violations of Bell’s Inequality suggest is that nature is non-local.
I believe that since the above posts were made, there has been significant progress in closing the loopholes that would still permit a local hidden variable theory. It’s still possible nature does employ hidden variables, but if she does, she does so non-locally.
I am a Learner with a capital ‘L’ when it comes to this area so forgive me if my question/comment is ridiculous, but here goes.
Is one possible answer to this anomaly (and various others I’ve heard of) that the whole cosmos down to its smallest particle exists within another ‘reality’ that has its own and different set of laws governing the behavior of its constituent parts? (and that includes our cosmos which is within the greater reality). If that were so then when we get down to the quantum level we are looking at the interface between the physical reality that we know and experience and this other greater reality. This ‘other reality’ can only be discerned when we come across these ‘odd behavior’ incidents. An oversimplification perhaps, but the existence of one ‘other and greater reality’ would maybe do away with the need to imagine the multiplicity of realities that have been posited by some leaders in the field.
Did the gravitons captured by LIGO reach us in a shorter period of time than expected? In other words did the gravitons traval faster than the speed of light?
Sometimes I wonder if the problem is not that of comprehending how a quantum world gives rise to the classical order. Or underlies it.
One cannot eliminate causality from the quantum world.
There is no instantaneous action at a distance ever.
Do gravitons travel faster than the speed of light?
There is said to be randomness and unpredictability in hidden variables. There is no such thing as randomness. The underlying principles simply are not known. Something is probable if it happens more often than not. What happens as seldom is designated as possible. Unpredictability is the inability to state with certainty the outcome of the measurement.
Hidden variable theory presupposes that the particles are in a definite state. How can randomness and unpredictability cause a definite state.
Einstein says that there is locality and realism.
BUT the violation of Bell = no hidden variables, non local, non realistic, and no communication between measurement sites.
Violation of Bell = completeness of quantum mechanics.
Is the measurement fixed and predetermined ot must one wait for the measurement?
There is no doubt that the particles are real and exist.
But in what state do they exist?
I think I am missing something because if you have hidden variables I would think one could not predict the outcome. Please solve this for me because I thought realism of Einstein was local and the measurement was fixed and determined meaning no hidden variables.
As far as something existing as a particle it is impossible for it to be in two places simultaneously.
Perhaps something does go faster than light.
Thank You
Comment from a working engineer, adhering to Newton’ s laws.
The very idea of incomprehensible results backed by instantly refutable ” statistics” is abhorrent to reality.
The questions reflect this sense of controlled confusion.
Newton laws work. Quantum physics is a idea of Einstien gone awry.
End