Q: Why are orbits elliptical? Why is the Sun in one focus, and what’s in the other?

Posted on August 18, 2010 by The Physicist

Physicist: This question always bothered me too. The short answer is: it falls out of the math. Specifically, the math of first year physics and second year calculus. The fact that the Sun is in one focus is just one of those things. It’s nothing special. Even less special is the other focus, which contains nothing at all.

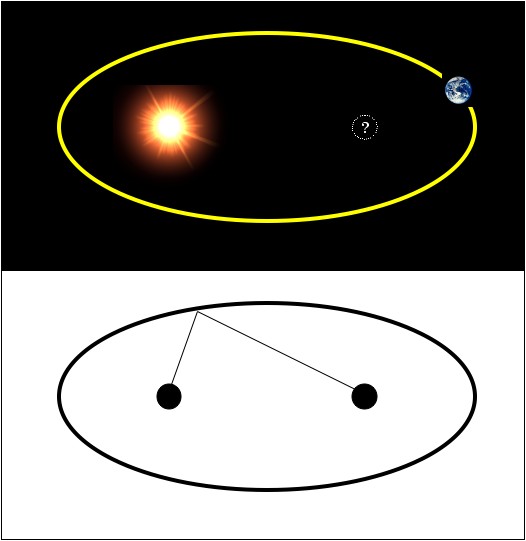
Ellipses and their foci have a lot of useful properties. It so happens that an orbiting object traces out an ellipse, with the thing it orbits around at one of the focuses. Coincidence? Yes.

I can’t find a good intuitive reason why orbits are elliptical. In fact, I can’t even find a mathematical derivation. So, because it should be found somewhere, I’ll leave the derivation floating in the answer gravy.

Answer gravy: The force of gravity is usually written as $ma=F=-\frac{GMm}{R^2}$ . You can rewrite this using vector notation as $m\ddot{\vec{x}}=-\frac{GMm\vec{x}}{|\vec{x}|^3}$ , where the dot on top is a time derivative. To keep the notation both standard and confusing, $\vec{x}=(x,y)$ .

$\begin{array}{ll}m\ddot{\vec{x}}=-\frac{GMm\vec{x}}{|\vec{x}|^3}\\\Rightarrow\ddot{\vec{x}}=-\frac{GM}{|\vec{x}|^3}\vec{x}\\\Rightarrow\dot{\vec{x}}\cdot\ddot{\vec{x}}=-\frac{GM}{|\vec{x}|^3}\vec{x}\cdot\dot{\vec{x}}\\\Rightarrow\dot{\vec{x}}\cdot\ddot{\vec{x}}=-\frac{GM}{(\vec{x}\cdot\vec{x})^{3/2}}\vec{x}\cdot\dot{\vec{x}}&\left\{\vec{x}\cdot\vec{x}=|\vec{x}|^2\right.\\\Rightarrow\frac{d}{dt}\left[\frac{1}{2} \dot{\vec{x}}\cdot\dot{\vec{x}}\right]=\frac{d}{dt} \left[\frac{GM}{(\vec{x}\cdot\vec{x})^{1/2}} \right]&\left\{\frac{d}{dt}\left(\vec{x}\cdot\vec{x}\right)=2\vec{x}\cdot\dot{\vec{x}}\right.\\\Rightarrow \frac{d}{dt}\left[|\dot{\vec{x}}|^2 \right]=\frac{d}{dt}\left[\frac{2GM}{|\vec{x}|}\right]\\\Rightarrow |\dot{\vec{x}}|^2=\frac{2GM}{|\vec{x}|}+c\end{array}$

c is an “integration constant“, it can be any number. Jumping over to polar coordinates $\left(\begin{array}{l}x=R\cos{(\theta)}\\y=R\sin{(\theta)}\end{array}\right)$ you can rewrite the usual velocity in terms of how fast you’re moving toward or away from the Sun $(\dot{R})$ and how fast you’re going around $(\dot{\theta})$ .

$\begin{array}{ll}\Rightarrow\dot{R}^2+R^2\dot{\theta}^2=\frac{2GM}{R}+c&\left\{\begin{array}{ll}|\vec{x}|=R\\|\dot{\vec{x}}|^2=\dot{R}^2+R^2\dot{\theta}^2\end{array}\right.\\\Rightarrow\left(\frac{dR}{d\theta}\dot{\theta} \right)^2+R^2\dot{\theta}^2=\frac{2GM}{R}+c&\left\{\frac{dR}{dt}=\frac{dR}{d\theta}\frac{d\theta}{dt}\right.\\\Rightarrow\left(\left(\frac{dR}{d\theta}\right)^2+R^2\right)\dot{\theta}^2=\frac{2GM}{R}+c\\\Rightarrow\left(\left(\frac{dR}{d\theta}\right)^2+R^2\right)\frac{L^2}{R^4}=\frac{2GM}{R}+c&\left\{R^2\dot{\theta}=L\right.\\\Rightarrow\left(\frac{1}{R^2}\frac{dR}{d\theta}\right)^2+\frac{1}{R^2}=\frac{2GM}{L^2R}+\frac{c}{L^2}\\\Rightarrow\left(\frac{1}{R^2}\frac{dR}{d\theta}\right)^2+\frac{1}{R^2}=2\alpha\frac{1}{R} +C&\left\{\begin{array}{l}C=\frac{c}{L^2}\\\alpha=\frac{GM}{L^2}\end{array}\right.\end{array}$

L is the angular momentum of the planet in question, and it’s constant. It may seem silly but, with the advantage of foresight, it’s better to solve this problem in terms of 1/R instead of R.

$\begin{array}{ll}\Rightarrow \left(-\frac{dS}{d\theta}\right)^2+S^2=2\alpha S +C&\left\{\begin{array}{l}S=\frac{1}{R}\\\frac{dS}{d\theta}=-\frac{1}{R^2}\frac{dR}{d\theta}\end{array}\right.\\\Rightarrow-\frac{dS}{d\theta}=\sqrt{-S^2+2\alpha S+C}\\\Rightarrow d\theta=\frac{-dS}{\sqrt{-S^2+2\alpha S+C}}\\\Rightarrow\int d\theta=-\int\frac{dS}{\sqrt{-S^2+2\alpha S+C}}\\\Rightarrow\theta+D=-\int\frac{dS}{\sqrt{C+\alpha^2-(S-\alpha)^2}}\\=\int\frac{\sqrt{C+\alpha^2}\sin{(u)}du}{\sqrt{C+\alpha^2-(C+\alpha^2)\cos^2{(u)}}}&\left\{\begin{array}{l}S-\alpha=\sqrt{C+\alpha^2}\cos{(u)}\\dS=-\sqrt{C+\alpha^2}\sin{(u)}du\end{array}\right.\\=\int\frac{\sin{(u)}du}{\sqrt{1-\cos^2{(u)}}}\\=\int\frac{\sin{(u)}du}{\sqrt{\sin^2{(u)}}}\\=\int du\\\Rightarrow\theta+D=u\\\Rightarrow\cos{(\theta+D)}=\cos{(u)}\\\Rightarrow\sqrt{C+\alpha^2}\cos{(\theta+D)}=\sqrt{C+\alpha^2}\cos{(u)}\\\Rightarrow\sqrt{C+\alpha^2}\cos{(\theta+D)}=S-\alpha\\\Rightarrow\frac{1}{R}=S=\alpha+\sqrt{C+\alpha^2}\cos{(\theta+D)}\\\Rightarrow R=\frac{1}{\alpha+\sqrt{C+\alpha^2}\cos{(\theta+D)}}\\\Rightarrow R=\frac{P}{1+\epsilon\cos{(\theta+D)}}&\left\{\begin{array}{l}P=\frac{1}{\alpha}=\frac{L^2}{GM}\\\epsilon=\sqrt{\frac{C}{\alpha^2}+1}\end{array}\right.\end{array}$

The choice of P and ε may seem arbitrary (and it is), but it has some historical relevance. P is called the “semi-latus recturn” and it basically describes the size of the orbit. ε is called the “eccentricity”, and it describes how lopsided the orbit is. ε=0 means the orbit is a circle, 0<ε<1 means the orbit is elliptical, and 1≤ε means that the orbit is open (not actually orbiting). For reference, the Earth’s eccentricity is ε=0.01671123 and Halley’s comet’s is ε=0.967.

D just describes what direction the far side of the ellipse points in, so it’s not actually important to the overall shape.

It turns out that this last equation relating R and θ is all you need to define an ellipse, such that the center of the system, (0,0), is at one of the foci. Here’s a proof:

An ellipse with a focus at (0,0) can be written $\frac{(x+F)^2}{A^2}+\frac{y^2}{B^2}=1$ where F is the distance from the center of the ellipse to the focus and $F^2=A^2-B^2$ .

$\begin{array}{ll}R=\frac{P}{1+\epsilon\cos{(\theta)}}\\\Rightarrow R+\epsilon R\cos{(\theta)}=P\\\Rightarrow \sqrt{x^2+y^2}+\epsilon x=P\quad\quad\quad\left\{\begin{array}{l}x=R\cos{(\theta)}\\y=R\sin{(\theta)}\end{array}\right.\\\Rightarrow \sqrt{x^2+y^2}=P-\epsilon x\\\Rightarrow x^2+y^2=P^2-2P\epsilon x+\epsilon^2x^2\\\Rightarrow (1-\epsilon^2)x^2+2P\epsilon x+y^2=P^2\\\Rightarrow x^2+2\frac{P\epsilon}{1-\epsilon^2} x+\frac{y^2}{1-\epsilon^2}=\frac{P^2}{1-\epsilon^2}\\\Rightarrow x^2+2\frac{P\epsilon}{1-\epsilon^2} x+\left(\frac{P\epsilon}{1-\epsilon^2}\right)^2+\frac{y^2}{1-\epsilon^2}=\frac{P^2}{1-\epsilon^2}+\left(\frac{P\epsilon}{1-\epsilon^2}\right)^2\\\Rightarrow \left(x+\frac{P\epsilon}{1-\epsilon^2}\right)^2+\frac{y^2}{1-\epsilon^2}=\frac{P^2(1-\epsilon^2)}{(1-\epsilon^2)^2}+\frac{P^2\epsilon^2}{(1-\epsilon^2)^2}\\\Rightarrow \left(x+\frac{P\epsilon}{1-\epsilon^2}\right)^2+\frac{y^2}{1-\epsilon^2}=\frac{P^2}{(1-\epsilon^2)^2}\\\Rightarrow \frac{\left(x+\frac{P\epsilon}{1-\epsilon^2}\right)^2}{\left(\frac{P^2}{(1-\epsilon^2)^2}\right)}+\frac{y^2}{\left(\frac{P^2}{1-\epsilon^2}\right)}=1\end{array}$

Put it all together, and you’ll find that this is definitely an ellipse with a focus at the point (0,0), the location being orbited around (like the Sun for instance).

This entry was posted in -- By the Physicist, Astronomy, Physics. Bookmark the permalink.

55 Responses to Q: Why are orbits elliptical? Why is the Sun in one focus, and what’s in the other?

Necat Taşdelen says:

April 9, 2016 at 6:32 pm

An e-mail is send to your address.A zero perpendicular force component create a Vp=Ct
Your affirmaton “A zero perpendicular force does not, and this is important, does not mean that the perpendicular velocity is constant. Imagine a particle traveling in a straight line ….” is wrong.Imagination of a straight line orbit is treated in my mail.I must repeat my question: how r*Vp=Ct1 exist together with r*Vp^2=Ct2 .Forget the configuration,the tricky geometry,see the math between these two Kepler’s affirmation:
r*Vp^2/(r*Vp)=Ct2/Ct1=Vp=Ct3.Then as Vp is constant,Kepler’s r*Vp is not correct. then elliptical orbits are wrong.The celestial motion equation is
r=-4*t^2+4*t*T-4*T^2/6 this is not an ellipse but a parabola on Cartesian or a spiral on celestial Polar.(x,y,z,time)
Pingback: Q: How can something be “proven” in science or math? | Ask a Mathematician / Ask a Physicist
Lucky says:

February 9, 2020 at 6:30 pm

Since L = r x p, why is there no sin(y) term included in the 2nd paragraph when angular momentum is introduced, where y is the angle between the tangential velocity of the planet and the position vector from the sun to the planet.
Error: Unable to create directory uploads/2024/12. Is its parent directory writable by the server? The Physicist says:

February 9, 2020 at 10:35 pm

@Lucky
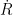It’s quietly hidden away in the definition $L=R^2\dot{\theta}$ . Since there’s no $\dot{R}$ involved, L is talking about only tangential and not radial velocity.
Ed Shields says:

September 28, 2024 at 5:58 pm

The sun is one of the foci for each plant. Do the other foci for each of the planets form a line? If so, is the any significance to this line?