Physicist: This question is especially perplexing after a first year physics course, where every question starts with “ignoring air resistance…”. There are a couple of different way to approach the answer, but I like this one best.
Way back in the day a dude named D’Alembert came up with the unsurprisingly named “D’Alembert’s paradox” which essentially says that in air and water an object traveling at subsonic speeds experiences neither drag nor lift. That’s obviously not the case which is why this is “D’Alembert’s paradox” and not “D’Alembert’s well known fact”.
The resolution is to take into account vorticity and the rotation of air flow around the object in question.
Rotation of air allows the air to flow faster over the top or the bottom of the ball. But a funny thing happens when air moves quickly; the transverse air pressure (pressure to the sides) drops. This effect is called the Bernoulli effect or, in certain cases, the Venturi effect.
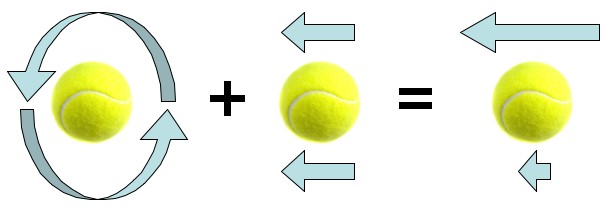
If you combine the flow of air rotating around a ball, with the flow of air past a ball, then the result is a faster flow past one side and a slower flow past the other side. In this example there is less pressure on the top than the bottom.
So how can you induce air to rotate around a ball in the air? Base balls, golf balls, and especially tennis balls are designed to have rough surfaces that grab the air a little bit. So if the ball spins as it moves it’ll drag the air around it a little, which leads to air rotating around the ball, which makes the air on one side move faster than the air on the other, which leads to a lower pressure on one side compared to the other, which creates a net force, which pushes the ball around.
So if you want the ball to curve downward you make it spin as though it were rolling away from you. If you want it to curve up (well… Stay in the air longer, no Human can make a ball actually curve upward in flight) you’d want the ball to spin as though it were rolling toward you. And of course, you can also make the ball veer left or right using the corresponding spin.







I thought I understood what makes a baseball curve by using the Bernoulli effect. But I realize I’m confused. In your diagram above, the air is moving faster over the top surface of the ball. In your diagram, it says there is less pressure on the top. That makes sense so far. But, less pressure on the top would tend to make the ball stay in the air longer. That’s the reverse of what is said in the last paragraph.
From experience, I know a baseball (any ball) will curve to the left when it is moving forward and spinning counterclockwise as viewed from above. Again, that seems to be the opposite of what Bernoulli’s effect would cause. I’m still confused or else your explanation is incorrect.
I dig!
The Bernoulli effect is caused by the velocity of the air passing by the ball itself, as opposed to by a particular piece of the surface.
The threads and bumps and imperfections on the surface of the ball grab the air a little and drag it around in the direction that the ball is rotating. So, in your example, when the ball is turning counter-clockwise it pulls the air around its left side a little faster. So overall the air is passing the ball on the left a little faster.
However, due to the spin, a point on the right side of the ball feels the air passing faster. But, the actual passage of air (regardless of cause, or how it feels to a point on the surface) is what’s important.
That trips me up too. Always have to take an extra minute.
Very useful
i am not satisfied with the above explanations
The idea of a ball rising may not be out of the question. I don’t know the formula, but according to the video you linked, the lift force from a baseball throw is already half the force necessary to hold up the weight of the ball.
Given that a tennis racket can apply more force and the ball is lighter…
Also being a tennis player myself, I can speak to what the baseball may have seen because it’s visible with tennis balls. The ball seems to suspends its downward trajectory until air drag lowers its forward velocity enough, at which point the ball falls almost straight down. This is the essence of the classic “drop shot.”
Given its exaggerated occurrence with a tennis ball, I wouldn’t be surprised if at least some of the air suspension were present with a baseball throw. In fact, perhaps with the right wind current, the ball might indeed appear to rise from the player’s perspective?
Er, would you mind replying to my above comment here? I didn’t notice the box to check for notifying me of replies via my email until after I hit post.
Another point: A ball hit with enough acceleration has its spherical form warped to an oblong. How would this interact with the bernoulli principle?
I believe it’s a well-known fact in soccer (football) that a ball kicked “flat”–no spin–will wobble side to side in the air. Maybe the spin helps it keep its shape, I don’t know, but if it doesn’t then maybe this is a consideration to make.
Bill Graham: I thin you’re getting confused by the arrows. So was I!
In that diagram the ball is moving from left to right, and has backspin. The arrows are the resulting air flow.
If the ball weren’t spinning, the air flow over the top and bottom would be the same (middle ball). If it were stationary but spinning, it would be dragging air to the left at the top, and to the right at the bottom (left ball). Add the two together, and the spin speeds up the air passing over the top, and slows down the air passing under the bottom (right ball). Result – it rises up (or at least drops less slowly).
If the ball had topspin, the big arrow (fast flow, low pressure) would be on the bottom – and the ball would dip, as you say.
So, from my understanding let me give you an example of a simple situation.
You drop 2 balls with equal mass and diameter.
Both balls are dropped from a release machine.
One of the machines, however, has a circumferential axis.
What would be the variable clockwise speed to actually slow the second ball from a straight gravity drop in compared to the other?
“No human can make a ball actually curve upward in flight”
→I can. A beach ball.
This phenomenon is summarized much better by the Magnus Effect.
http://en.wikipedia.org/wiki/Magnus_effect
So, as I understand what you’re saying, the spin of the ball drags air around with it which exceeds the overall passage of air in relation to its linear direction, lessening the pressure in the direction of the spin. Does that sound about right?
In a video demonstrating the magnus effect a basketball with a backspin was dropped from a 400′ high wall. The reverse spin caused the ball to curve away from the wall, and actually appeared to curve away at a faster rate as it dropped. So I wondered if the air flow over the ball actually caused it to spin faster as it fell. Normally I would have expected the spin to slow down due to air frictional losses.
Tony is right, the explanation is as described for the Magnus Effect. It’s not simple at all. The air velocity RELATIVE TO THE SPINNING BALL is higher on the side spinning into the flow, e.g., on top for top spin. This causes the turbulent boundary layer (insured by the rough surface) to separate earlier on that side than the other. This causes the turbulent wake to move around in the direction of rotation (upward for top spin, downward for back spin). The result is a flow pattern for the air outside the wake that looks like it’s going over a wing, BUT right-side-up for back spin (lift) and upside down for top spin. The air outside the wake, follows this wing shape and has the expected pressure variation so that top-spin pushes the ball down (upside-down wing) and back-spin pushes it up. The result is opposite of what most people think intuitively.
so still, i understand the impact of magnus and bernoulli, but linguistically speaking, has the course of a thrown ball’s “curve” be truly described as changed? isn’t the ball already going to travel a certain course given the principles above? if there is not outside object acting upon the ball, it will continue to travel in the direction it was throwN?
More Magnus effect….less Bernoulli effect!
More momentum conservation…less pressure differential!
Bernoulli describes pressure changes along a streamline not between streamlines as I understand it. So though I do not doubt that there is greater pressure below than above, I think more of the curve is due to more turbulence and early separation of air along the fast moving (relative to the air) surface and more laminar flow, and therefore later separation of air, along the slower moving (relative to the air) surface. The non-separated air then curves around the back of the ball LONGER changing the direction of the air molecules. The ball pulls the non-separated air sideways and, likewise, the air pulls the ball the other way.
Differential pressure certainly plays a part…but conservation of momentum is the star.
What will be the formula of maximum height and total flight time of a golf ball hit with spin in a vacuum having no air friction and wind speed etc. It will have 3 D projectile motion if it is hit with spin.
Will it be same ( h= 1/8 gt^2 ) as it is in 2D projectile in vacuum having no spin.
This explanation is over simplified and states some common Bournoulli fallacies about speed vs pressure. The speed of air does not determine pressure. It’s the pressure difference that causes speed changes of the air. It is not a one or two line explanation but for those that want to understand what 8s happening with baseball’s, sails, wings, etc read the entire explanation here. It will likely differ than what you were taught in high school or uni about speed and pressure.
Give a read and then figure out for yourself why top spins go downward 🙂
https://www.quora.com/q/kyuoyckftflurrpq?ch=10&share=6f357b59&srid=5RhPI
There is the link!