Physicist: Nopers!
The Heisenberg uncertainty principle, while normally presented in physics circles, is actually a mathematical absolute. So overcoming the uncertainty principle is exactly as hard as overcoming that whole “1+1=2” thing.
The uncertainty principle (the “position/momentum uncertainty principle”) is generally presented like this: you have some particle floating along and you’d like to know its position and its momentum (velocity, whatever) so you bounce a photon off of it (“Bounce a photon off of it” is just another way of saying “try to see it”). A general rule of thumb for light (waves in general really) is high frequency waves propagate in straight lines, and low frequency waves spread out. That’s why sunlight (high frequency) seems to go in a perfectly straight line, but radio waves can spread out around corners. For example, you can still pick up a radio station even when you can’t see it directly.
So, if you want to see where something is with precision you’ll need to use a high frequency photon. After all, how can you trust the results from a wandering, low frequency photon? But, if you use a precise, high-frequency, and thus, high-energy photon, you’ll end up smacking the hell out of the particle you’re trying to measure. So you’ll know where it is pretty exactly, but it’ll go flying off with some unknown amount of momentum. Any method you can come up with to measure the momentum will require you to use low-frequency, low-energy, gentle photons. But then you won’t be able to figure out the particle’s position very well.
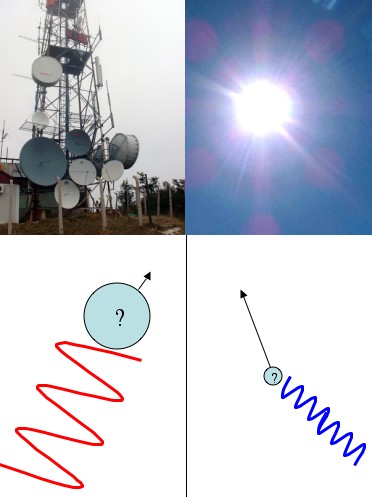
Low frequency photons (like radio waves) don't tell you much about where a particle is, but they doesn't knock it around much either (so you can measure its momentum better). High frequency photons (like sunlight) are terrible at measuring momentum, but can tell you position well.
So far this seems more like an engineering problem than a problem with the universe. Maybe we could arrange things so that the high frequency photon hit softer or something? There was a lot of back and forth for a long time (still is in some circles) about overcoming the uncertainty principle, but in the end it can never be violated.
Rather than being something that’s merely very challenging like, “you can’t break the sound barrier”, “what goes up must come down”, and “you can’t be the world’s best kick-boxer and be the world’s most handsome physicist”, the uncertainty principle is a mathematical absolute. So, unless the basic assumptions of physics are completely wrong (and they’ve held up to some serious scrutiny), the uncertainty principle is in the company of things like “you can’t go faster than light”, “energy and mass are conserved”, and “modern mathematicians don’t have beards” (has anyone else noticed this?). What follows is answer gravy.
Answer gravy: This gravy has some lumps. If you know what a “Fourier transform” is, and are at least a little comfortable with them, then this could be interesting to you.
The square of a quantum wave function is the probability of finding it in a particular state. For example, the “position wave function” can tell you the probability of finding a particle at any position. To get the probability from the wave function, all you have to do is square the wave function.
If you’ve got the quantum wave function for the position of a particle, then you can find the the momentum wave function,
, by taking the Fourier transform of f. That is,
. Now, you can define the uncertainty as the standard deviation of the probability function, which is a really good way to go about it.
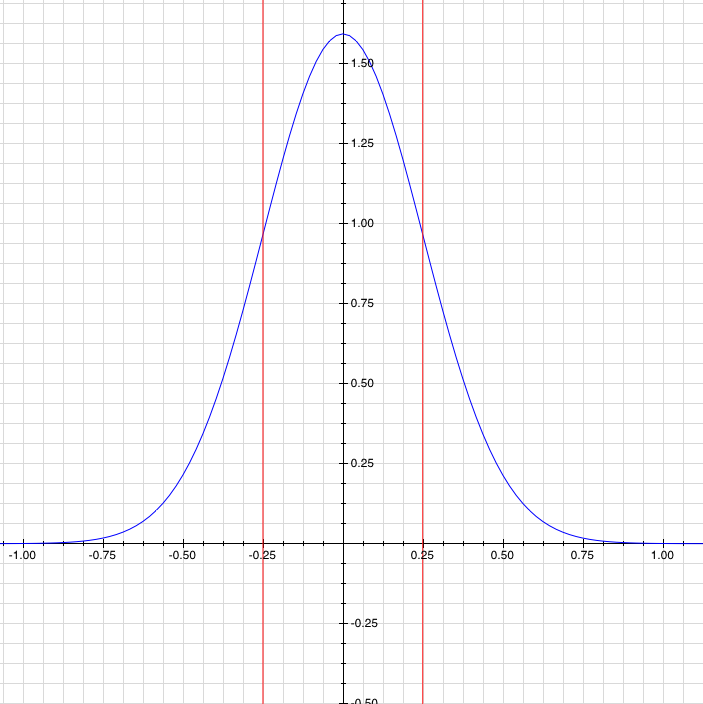
A probability function (blue), with its uncertainty or standard deviation (red). Like you'd expect, the particle is most likely to be near zero, but it's not certain to be near zero.
The uncertainty principle now just boils down to the statement that the product of the uncertainties of the square of a function, , and the square of its Fourier transform,
, is always greater than some constant. In what follows you’ll find some useful stuff such as Plancherel’s theorem and Cauchy-Schwartz.
So, there’s the Heisenberg uncertainty principle: . A physicist would recognize this as
. The difference comes about because the Fourier transform that takes you from the position wave function to the momentum wave function involves an
, and
. (For the physicists out there who were wondering what happened to their precious h’s)







Thanks for posting this! I’ve heard of the Uncertainty principle before, but I’ve never heard why it is so. The business about the different types of waves measuring different things and affecting the particle differently is really simple to understand.
Pingback: Q: How do surge protectors work? « Ask a Mathematician / Ask a Physicist
it seems to me that you are explaining the uncertainty principle as a limitation of our ability to measure the particle without using photons. this sounds like if you could just find another way to do the experiment then you wouldn’t have the problem. but that implies that uncertainty is not an absolute its just the best we can do so far…
The photon measurement thing is a symptom of a more fundamental problem. It makes no difference what method you use.
A better way to think about the problem is to say “the particle doesn’t have a definite position that can be measured”, as opposed to “it’s hard to measure stuff right”.
Does superstring theory allow for some hidden order to this apparent quantum randomness or indeterminability?
i m so much thankful to you for this and also i would like to say that this limit cannot be avoided becouse uncertanity has a great role in the creation of this universe…… further perfection in this world is impossible….
why can’t you fire a photon of a specific energy at the particle, then when you collect the photon (showing you where the particle was) also record some change in the photon (wavelength or frequency or energy) that could be related to how much momentum the particle has?
That’s basically exactly how you do it.
Although it works very well (the uncertainty is a very small quantity), it can’t work perfectly. Keep in mind that the uncertainty principle applies to everything, including the photon being used.
couldnt you fire a low frequency photon and a high frequency photon at the measured particle simultaneously. so you get a position measurement from before its momentum was disturbed, and a momentum measurement? or i guess the problem with that is you would get an accurate view of what the particles position and momentum WAS exactly, but the information would be outdated as it would then have a different momentum? dont neutrinos have a small chance of interacting with a thing? could you somehow fire trillions of neutrinos at the particle until one hits to measure its momentum and position without disturbing it? or would that still disturb it by some tiny amount thus meaning a bit of uncertainty? or, if all matter or energy generates some amount of gravitational pull, could we develop equipment that responds to extremely (EXTREMELY) small gravitational pulls, allowing us to measure the particles position and momentum without actually doing anything to it? or maybe im just dumb and missing something.
Same sorts of problems. Dozens of ideas were proposed back in the day, but rather than go through them one at a time, Heisenberg wrote the uncertainty principle mathematically. Any method you use that obeys quantum mechanical laws (every method) will suffer from the same limitations.
I understand the uncertainty principle as a product of observable and measurable characteristics, but at a fundamental level… does that mean that any particle doesn’t exhibit an absolute pairing of characteristics (momentum vs position etc…)? just because it can’t be observed or measured accurately, doesn’t mean that it doesn’t exist in absolute measure.
I’m only asking because i’ve seen the uncertainty principle used to argue a finite arrangement of particle assemblies within a closed system.
That was the crux of a debate between physicists for decades. But the answer is: no, nothing can exist in a definite position with a definite momentum. It’s built into the nature of things, as opposed to being built into the nature of measurement.
Pingback: Q: What is “spin” in particle physics? Why is it different from just ordinary rotation? | Ask a Mathematician / Ask a Physicist
Pingback: Q: Is there some way to actually play quidditch? | Ask a Mathematician / Ask a Physicist
Pingback: Q: What are singularities? Do they exist in nature? | Ask a Mathematician / Ask a Physicist
at the microscopic level,, cant we consider the photon-electron collision to be perfectly elastic and thus easily calculate the momentum change knowing the energy of the photons used and thus solve the values for what should be the actual position and momentum of electron as compared to observation???
also,, why cant we first measure x with high precision and then v and compile the results to get accurate results
Pingback: Q: Why don’t “cheats” ever work on the uncertainty principle? What’s uncertain in the uncertainty principle? | Ask a Mathematician / Ask a Physicist
I thought you could overcome the uncertainty principle if you fired two particles with the same speed in opposite directions. To put this another way, fire one of the particles with a negative velocity, but equal speed to the first particle. Then you can find out the velocity of one and the position of the other, and then you know the velocity and position of both.
Not even then, unfortunately.
Please can anyone help me by posting the full derivation of the heisenberg uncertainity principle using sine wave function (y(x,t)= A sin(kx-wt)) and also how to write a sine wave function in terms of fourier series?
Can you really validate this with certainty if the uncertainty principle exists? Please cite any research you know of actually proving this statement as it sounds like bias rather than knowledge.
[in regard to: ” just because it can’t be observed or measured accurately, doesn’t mean that it doesn’t exist in absolute measure.”]
‘The Physicist’ says:
That was the crux of a debate between physicists for decades. But the answer is: no, nothing can exist in a definite position with a definite momentum. It’s built into the nature of things, as opposed to being built into the nature of measurement.
It is basis dependent. The traditional uncertainty relation is based on basis function consisting of sine and cosine functions multiplied with e^(-c*x^2).
Change that and get different uncertainty relations. According to the spectral theorem no basis is preferred, all are transformable to each other, so no one can say that there is a preferred basis.
There are also examples from reality of beating the relation approximately 10 times, see for example Majka et.al. Hearing overcome uncertainty relation and measure duration of ultrashort pulses, Europhysics news 46(1):27-31 · February 2015 ( DOI: 10.1051/epn/2015105 ) http://epn.eps.org/EPN%2046-1#p=28
Entangled pairs though.
Pingback: Q: Can you beat the uncertainty principle using entanglement, by measuring position on one particle and momentum on the other? | Ask a Mathematician / Ask a Physicist