Q: If you were on the inside of the Sun falling in, the matter closer to the surface doesn’t affect your acceleration, but the matter closer to the core does. Why is that?

The original question was: Plait talks about the “physics of solid bodies” and why, specifically, if you were on the inside of the Sun falling in, the matter “behind” you- closer to the surface- doesn’t affect your acceleration at all, and all that matters is the matter “in front” of you- closer to the core. Why is that?

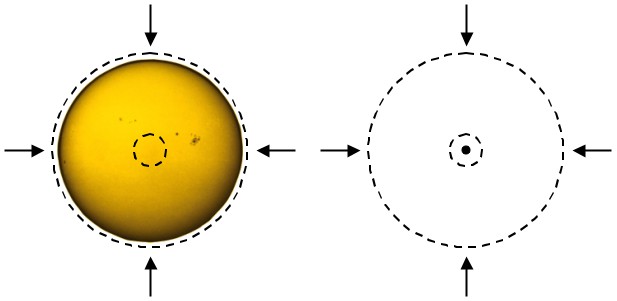
Physicist: The short, uninteresting answer is that the gravity from any layer above you cancels itself out. If you take any sample layer above you, and you happen to be closer to one side, then you’ll find that the side you’re closer to has more pull on you, but there’s less of it. Conversely, the far side has less pull, but there’s more of it. For a sphere (but not a ring) these forces cancel exactly. So as you fall in you can ignore all the layers above you.

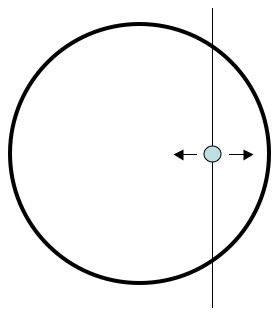
Pick a layer. Anything inside will experience exactly the same amount of pull in every direction, and so, no pull at all.

Answer gravy: One of the greatest tools in the physicist’s tool kit is “Gaussian Surfaces“. They let you shortcut really difficult math problems using pictures and a little reasoning.  Even better, you come across smarter than perhaps you deserve, which is a big plus.

A Gaussian surface is nothing more than an invisible bubble that you draw in space. The “inverse square law” of gravity can actually be rewritten as “the total amount of gravity pointing into the bubble is proportional to the amount of matter inside the bubble”. The arrangement of matter (both inside and outside the bubble) certainly changes how gravity points into (or out) of the bubble, but the total amount of gravity pointing through depends only on the amount of matter inside.

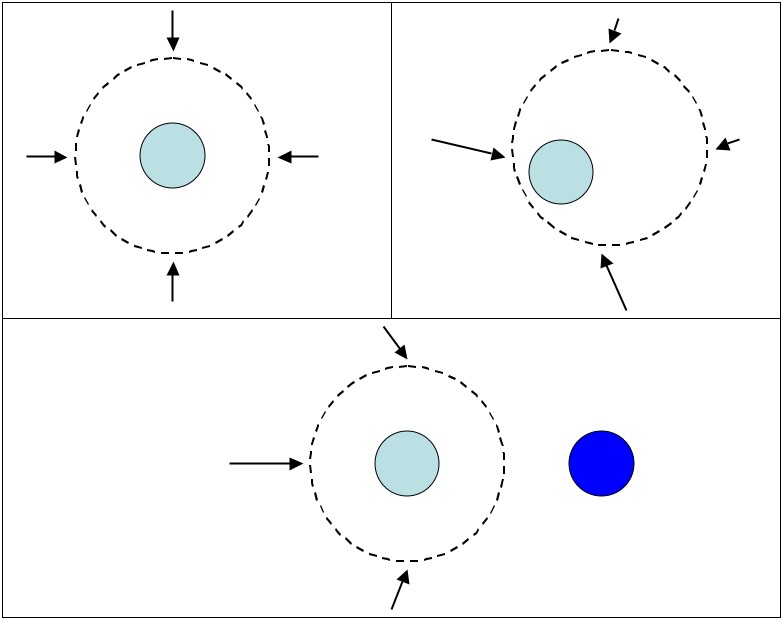
(upper left) when the mass is symmetrical and in the middle, then the gravity is exactly the same everywhere on the surface. (upper right) if the matter is off to the side, then gravity will be stronger, or weaker, or point in different directions at different points on the surface, but the total stays the same. (bottom) matter outside of the Gaussian surface can affect how gravity pokes through, but it can't affect the total.

Now say that your bubble is an exact fit around a sphere of matter. Everything is perfectly symmetric, so there’s no reason for gravity to be any stronger or weaker anywhere and, given the amount of mass inside the sphere, you can figure out how strong the gravity is. Now say you add more matter, but uniformly, on top of your original sphere.

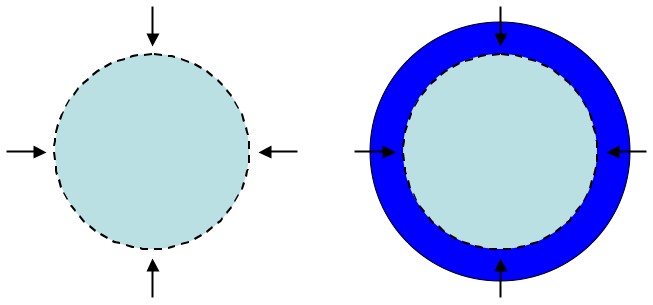
In both situations the total amount of matter inside the bubble is the same, and everything is nice and symmetrical, so the gravity along the surface of the bubble is the same.

The matter inside the sphere has remained the same, so the pull at the surface of that sphere remains the same. As a result, so long as the matter above is at least fairly symmetrical (which is the case for any planet or star you can think of), you can ignore the layers above the surface of the bubble.

Specifically, as you fall farther and farther into the Sun (or Earth, or whatever else is round) you can figure out how much gravity you’re feeling by using a Gaussian surface, for which you only need the matter below you. The layers above will exert no pull on you, and you will exert no net pull on them (for every action/force there is an equal and opposite reaction/force).

This part has nothing to do with the question: You can use Gaussian surfaces to prove some surprising things. Specifically: Dyson spheres work, and black holes have no more gravity than the stars they came from.

From the last argument (above) you know that the layers above you have no net gravitational effect on you. But what if you fall a little way into a planet, and suddenly find that the inside of it is completely hollow? One you’re inside all the layers are layers above you. So there’s no gravity at all inside of a large hollow sphere (at least, none caused by the sphere). If you built a really huge sphere around a star you’d have a “Dyson’s sphere”. The sphere doesn’t pull the star, and the star doesn’t pull the sphere. It’s stable no matter where the star is inside the ball. So long as no one shoves anything, everything will just float neutrally right where it is.

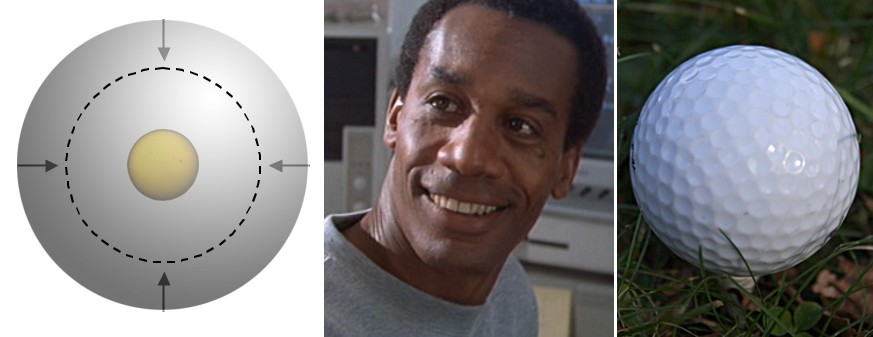
(left) the set up for a Dyson Sphere. The perfectly spherical shell has no gravitational effect on anything inside the sphere, including the star, and vice versa. (center) Miles Dyson, inventor of the Dyson sphere, and future inventor of Skynet. (right) an artist's interpretation of a Dyson sphere.

Now, put a Gaussian surface around a star. There’s a certain amount of matter in the star, and that tells you how much gravity is pointing through the surface. If the star shrinks, who cares? Same amount of mass = same amount of gravity.

The gravity through the outer Gaussian surface stays the same, since both contain the same amount of matter. The gravity through the inner Gaussian surface increases dramatically after the star collapses, because it contains all of the star's mass, instead of just a small part of it.

But if you draw a small Gaussian surface around the core of the star you’ll find that the gravity along the surface is small, because there is (relatively) little mass inside of it. If for some reason you found yourself in the center of the Sun, you’d be floating in zero G’s. Point of fact; you’d also be on fire.

Now when the Star collapses, all of the matter is drawn into a tiny region. Both spheres (see diagram on the right) now contain all of the star’s matter, and thus the same total amount of gravity pokes through them. The only difference is that the inner sphere is smaller, so the gravity has to be more intense to get the same total as the outer sphere.
Black holes do have very intense gravity, but only in the region where the star used to be.