Physicist: The golden ratio, g, is 
The golden ratio is defined in many (equivalent) ways but the best known is: if A and B are two numbers such that the ratio of A+B to A is equal to the ratio of A to B, then g=A/B.
A rectangle, where the ratio of the long side to the short side is g, is called the “golden rectangle”. The ancient Greeks, being creepy numerologists with nothing better to do, were really excited about the golden rectangle and worked it into a lot of their art and architecture.
The Golden Rectangle: Clearly, it's the most perfect rectangle ever.
Setting the ratios equal to each other you can solve for g (approx. 1.62):
It’s this definition, the solution of this equation (0=x2-x-1), that is usually the vehicle that brings g into the conversation (In math circles they usually say “mathversation”). Or, to put it another way, it shows up by coincidence.
For example; the Fibonacci sequence is a string of numbers, F0, F1, F2, … such that FN = FN-1 + FN-2 and F0 = 0 and F1 = 1. You can see quickly that the string of numbers is 0, 1, 1, 2, 3, 5, 8, 13, 21, …
It takes a bit of work, but (after some math happens) it turns out that 
“g” showed up a lot for the ancient Greeks because they spent a lot of time playing around with straight edges and compasses. The equation that describes a circle is quadratic, and the equation that describes a straight line is linear. So when you’re trying to figure out where an intersection is, or how long a line segment is, you’ll be solving quadratic equations and “0=x2-x-1″ (being simple) is one of the equations you’ll frequently see.
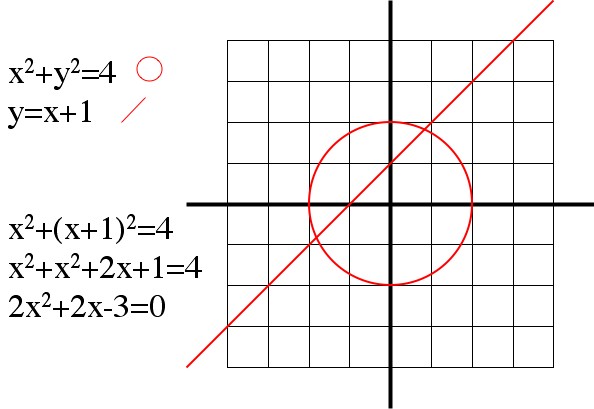
One example of the relationship between straight-edge-and-compass geometry, and the exciting world of quadratic equations.
Finally, g showed up again a couple hundred years ago in the study of “continued fractions“. However, I personally have only seen continued fractions used exactly once (in the context of rational number approximation) and g was no where to be seen. The numbers that mathematicians are most excited about these days are: 0, 1, e, and π.
Pingback: Q: Is there a formula to find the Nth term in the Fibonacci sequence? | Ask a Mathematician / Ask a Physicist
thank you for that explanation of the golden ratio! I fully understand it now! I advise you to not use the d word!
awesome loooool
I still don’t understand it…… And I’m using the d word 🙂
Can someone just put this in layman’s terms, I’m lazy and the whole reason of asking a mathematician is so the mathematician does the work, I just simply want to understand the concept.
Can someone simply provide a dimensioned example of a golden rectangle and give a simple explanation of how to make a golden triangle? Is [a] the short side or is [a] the long side, like: a = 1.62, and b = 1
Maybe all one has to do is to say, take the length of side [b] and multiply it times 1.62 to determine the length of side [a], or take the length of side [a] and divide it by 1.62 to determine the length of side [b]
How simple is that? … duh, or maybe just say the ratio is 1.62:1
But to say this is a perfect rectangle is pure garbage, maybe for a coincidence in math, but not for any other useful purpose, other than aesthetics, but beauty is only in the eye of the beholder.
KISS
It’s easily said that the golden number represented by the Greek symbol phi (Φ) and it’s value is approximately equal to 1.618; this is an irrational number and the decimal will need to be rounded-up at point in the infinite decimal stream.
This is for the layperson (like me) who needn’t be bothered with lengthy equations to draw an aesthetically perfect rectangle.
Φ (phi) is used to determine the aspect ratio (1.618 : 1) of the golden rectangle
To determine any scale of the golden rectangle, you simply multiply the length of the short side by 1.618 to determine the length of the long side, or if you want to determine the length of the short by the length of the long side, then divide the length of the long side by 1.618 to obtain the length of the short side.
What is so nice about the golden rectangle, is that if you cut a square out of it, what remains is also a golden rectangle. That is because in the original rectangle, B = A*(1+sqrt(5))/2. The new rectangle’s shortest side (C) is then B-A = A*(sqrt(5)-1)/2. Now, the relation between the sides of this new rectangle is A/C, which again is (1+sqrt(5))/2.
To find the Golden ratio or Golden Number or Golden rectangle. Take the width of something and divide it by 1.62. For example, if the width of your house is 30′ and you want the center beam height to be the golden number the center beam height should be 18.5′. 30 divided by 1.62 = 18.5′