The original question was: I was reading an article by Lijun Wang the experiment I think is called the NEC experiment. Basically what the guy does is speed up light so that it goes faster than the than the speed of light. If anything goes faster than light does that mean it goes backwards in time? Is this experiment genuine?
Here’s a description of the experiment.
Physicist: This experiment showed up in the popular media about ten years ago, and it’s still bothering people today. The very short answer is: nope! No physical object ever travels faster than light, and yet the experiment is real. This is pretty tricky, but it comes down to a distinction between “phase velocity” (light speed, “c”) and “group velocity” (depends on the medium). The experiment essentially requires a “standing wave” in the test chamber, with waves at many frequencies. These light waves interact in such a way that they create peaks, like when you pluck two slightly-out-of-tune guitar strings and you hear a pulsing sound. These peaks are usually called “wave groups” or “wave packets”. The peaks move around, and you can more or less keep track of where they are (more exactly; you can infer where they were after the fact). The pivotal point is that the experiment isn’t about turning on some kind of laser, that sends out a pulse, that suddenly moves faster than light. The experiment is about peaks made out of standing waves, and the standing waves are already all over the inside of the test chamber when the experiment begins. In the middle of the camber is a specially constructed cloud with extremely weird and strong optical properties, that changes how fast light of various frequencies move through it (slowing only, but to various degrees). Specifically, the lower the frequency, the slower it’s allowed to propagate through the cloud. This is a weird set up, and it’s difficult to produce.
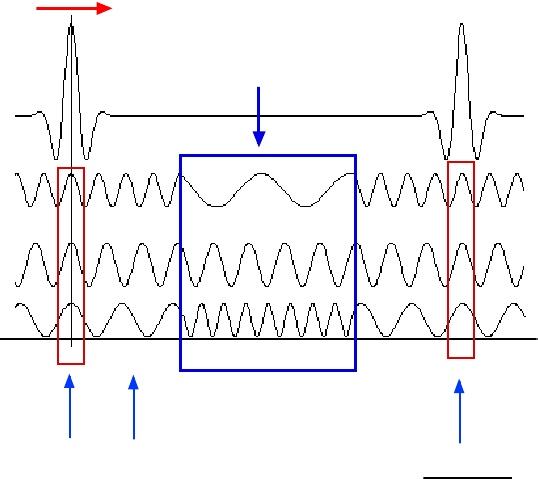
Waves of different frequencies travel at different speeds and that gives rise to "groups" or "wave packets". The red boxes are examples of how waves of different frequencies can add up. The blue box shows what happens to various waves as they pass through the cloud.
The above image was jacked from the original author’s follow up explanatory paper. A good estimate for the group velocity in general is 
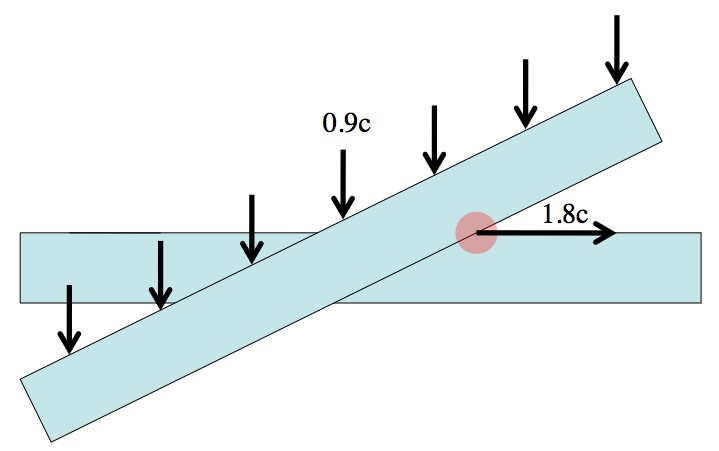
Nothing can physically move faster than light. However, abstract points, like the point of intersection or even the peak of a wave packet, can move as fast as they want.
This NEC thing is a similar “paradox”. And again, the author was kind enough to explain this whole thing here. To answer the follow up, “does going faster than light mean you go back in time?”: maybe. Probably. But, it’s never come up.
About the scissors paradox… Couldn’t that point of intersection push an object in front of it, giving it it’s speed?
Assuming that the scissors are made of an infinitely strong material, and the object is made of an infinitely strong material, and there’s an infinite amount of energy available (technically, more than infinite, whatever that could mean), then yes: the object in question would absolutely move faster than light, and you’d have all manner of weird paradoxes to worry about.
However, “in practice”, something would break long before the object got near the speed of light. The quick and dirty way to think about it is that the amount of energy required to accelerate anything to light speed is infinite, but the amount of energy needed to break any particular thing is finite.
Indeed, the scissors paradox does not produce the faster-than-light speed in a usual sense, i.e. does not allow to carry an information. With one exception, however. Namely, it can be used in a synchronization procedure, different from the Einstein’s (light) procedure, based on the light postulate. Let A and B lay on the path of displacement of intersection point. When the intersection point passes the point A, a clock is adjusted for time “zero”. Then, at point B, distanced from A at S, another clock is adjusted for time “zero+S/v”, where v is the speed of displacement of the intersection point. Since, at least theoretically, v may tend to infinity, then B synchronization time is closed to “zero”, so that we obtain an almost “immediate” synchronization procedure, independent from the SR light postulate. This opens new possibilities, questioning the light postulate and the resultant relativity of simultaneity. In my opinion, this provides us with an argument in favor of the otherwise self-consistent preferred frame theory.
Hope to get your response.
Maciej Rybicki
The important thing is that A can’t use the effect to send a signal to B faster than light. This situation is essentially the same as A and B getting a signal from somewhere off of the line between them, C, at a speed less than or equal to light speed.
That is, whoever sent the “upper blade” is the only thing actually sending a signal, A and B are just receiving it. So, while A and B can both take advantage of the signal from C, they can’t “piggyback” a new signal on it to communicate with each other.
I agree that A can’t use the scissors effect to send a signal to B. However, synchronization of A and B clocks does not require sending an intentional information. The sufficient is if initial conditions are settled, which means that A and B arrange to adjust their clocks according to the recipe given in the previous comment. What they must know is the velocity (v) of displacement of the intersection point (they can deduce it from the angle between the blade and the line connecting A and B, and from the vertical speed of falling).
Provided v>> c, this kind of synchronization becomes independent from the light postulate and, in fact, enables to verify this postulate by measuring the one-way speed of light. When applied to the systems being in relative motion (like the train and platform in the known thought experiment), the “scissors” synchronization procedure leads to conclusion of the absolute simultaneity, a different one-way speed of light, and all other properties describing the preferred frame theory.
You’re right, it does specify a frame. But if you want a new frame you just need new scissors.
Well then. Let the observers in two inertial frames S and S’ have their own identical superluminal scissors. Let us assume (for a while) the relativity principle to be in force. When S and S’ execute the scissors’ synchronization in their frames, it will turn out that the difference between indications of respective clocks (say, e.g. the “left” ones), simultaneous in S and S’ with the “right” clocks, will be much smaller compared with that obtained in light synchronization performed according to the light postulate. Consequently, when v tends to infinity, the difference vanishes, i.e. the simultaneity becomes absolute. It follows therefore that scissors synchronization leads to questioning of both the light postulate and the relativity principle.
There’s no problem with synchronizing clocks in general. For a given frame you can certainly define simultaneity, which is what your example is talking about.
With regard to simultaneity, the only statement that relativity makes is that the same notion of simultaneity can’t be defined across different frames.
In relativity, the relative simultaneity is a consequence of the light postulate. Instead, in the preferred frame (PF) theory, the speed of light is defined as (c-u)gamma^2, in the direction of motion of the reference frame against PF, and (c+u)gamma^2, in the opposite direction ( c – the speed of light in PF, u – velocity of the reference frame against PF, gamma – Lorentz factor defined against PF). The consequence of the so-defined speed of light is that simultaneity is absolute.
From my example it follows that, for v tending to infinity, the same notion of simultaneity is defined across different frames, which means that scissors’ synchronization reveals an absolute simultaneity.
I do see how the scissors here can synchronize two clocks. But regardless of how the clocks are synced up, a differently moving observer will see them not synced. In the case of you example, the infinite speed case corresponds to the upper blade not being angled at all, and just passing A and B at the same time (from their frame). An observer traveling in the A-to-B direction would see the blade tilted such that it got to A first, and an observer traveling in the B-to-A direction would see the blade tilted such that it got to B first (there’s an old post here that talks about that a bit).
If by “light postulate” you mean the idea that the speed of light is the same to everyone, then you’re absolutely right about that leading to the relativity of simultaneity. But it’s not a guess, it’s been experimentally verified up one wall and down the other, and it’s what led to relativity. The preferred frame theory is essentially what relativity was brought in to replace.
Let me focus first on the second paragraph…
Of course, by the light postulate I mean the second STR postulate. Can you specify by what experiments has it been verified? Both Michelson-Morley and Kennedy-Thorndike experiments confirmed the averaged two-way (in general, on closed path) constant speed of light only. Likewise, as far as I know, not any of the measurements of c-value refers directly to the one-way speed. Thus, in STR, the constant one-way speed of light has a status of an axiom (a postulate) not an experimental fact.
According to PF theory, the light pulse does not form a spheroid (as STR predicts) but an ellipsoid. Although, in most cases (i.e. except the crosswise direction to the frame motion) the one-way speed of light is different from c, yet the two-way speed (on closed path) is always c as it is in STR. Thus, PFT explains these experiments as well as STR.
Instead, in the first paragraph, you describe in short the STR mechanism of simultaneity (which I understand), obvious in the framework of STR, but not necessarily obvious by itself.
With all of that, I must consider in details the question of scissors’ synchronization in its relation to simultaneity, which may take some time. Of course, I will be grateful for your response to this comment.
Physicist who understand Einstein do not understand physics.
Every charged particle can be very simple accelerated also thousand times faster than light. See: https://petarbosnicpetrus.wordpress.com/2014/05/18/346/
Expectations in regard to accelerator capable to accelerate particles many times faster than light are supported by experimental experience. See the escape of particles along the axis of linear fusion reactors which had to be prevented by miror electromagnets. Particles escape along the axis because of scissors effect. See https://www.youtube.com/watch?v=Q5JtELLRZz8 Imposibity of FTL velocities does not exist in nature than rather in dogmatic human brain.
Responses of physicist are ridicules. The linear nuclear fusion reactors are in fact two electromagnetic scissors faced one to an other. When their coils are switching on, its waves are not snipping plasma, than rather push it, compress and provokes nuclear fusion.
Believing to physicist, experiments by linear fusion reactors voulld be fair tailes.
Pingback: Q: Is darkness a wave the way light is a wave? What is the speed of dark? | Ask a Mathematician / Ask a Physicist
So a way non physicist or even educated.
This article in its explanations and QnA seem to have several times said the speed of light is not constant. It can be changes and is dependent on outside variables from the light itself. What does that do for all the equations that require a constant speed of light. Is physics turned upside down?