Physicist: Feynman diagrams are primarily a way to keep track of what you’re doing. Physicists aren’t geniuses or anything, and they get distracted pretty easily.
When you’re trying to calculate the probability of a particular particle interaction you’ll find yourself integrating over (adding up) every possible position and momentum of every involved particle. Moreover, when there are several different ways that you can get a particular result you need to keep track of all the different ways that the result can happen.
Feynman diagrams are not technically necessary, but they do help you keep track of variables and permutations. It turns out that particle physics is a lot more complicated than you’d think. That holds true even if you think it’s really, really complicated.
Feynman diagrams were created alongside the field of quantum electrodynamics and (as far as I know) no one has suggested another diagram system (if it ain’t broke…). They allow you to write down the important integrals in the form of a picture, which makes them far more understandable to just about anybody.
Ultimately, once a diagram has been made, and an integral is created and evaluated from it, you end up with the probability amplitude of that particular particle interaction taking place.
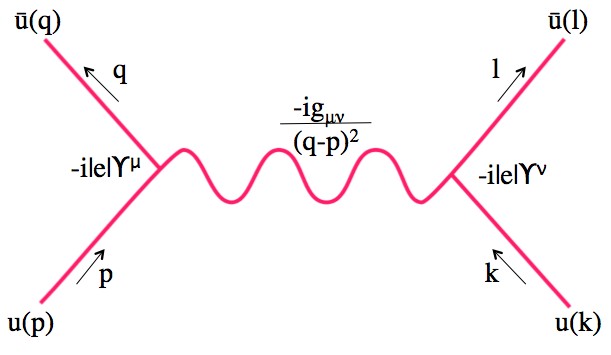
The Feynman diagram for the Coulomb interaction (electric force), along with the parts of the Feynman integral they correspond too. Every part of this is really nasty. For example, that "g" is actually 16 numbers.
The electric force (what physicists call the “Coulomb force” to look smart) is mediated by photons. That is to say, particles with charge push or pull on each other using photons. The diagram above is the “first order Feynman diagram” for two electrons repelling each other. The probability amplitude of two electrons with momentum p and k pushing off of each other and flying off again with momentum q and l is given by:
The squiggly line is the exchanged (virtual) photon and the solid lines are the electrons. The diagram generally represents time as the vertical direction and space as the horizontal, but it turns out that on extremely short time and distance scales it’s not super important.
If you’re wondering which particles are virtual and which are real: virtual particles are the ones stuck inside the diagram and real particles are the ones going in and coming out (they might go on to be detected somewhere).
The reason this is a “first order” diagram is because this isn’t the only way this interaction can happen, merely the most likely. The less likely interactions are also all happening at the same time, they just have less weight. Super-positions and whatnot. Quantum mech is good fun.
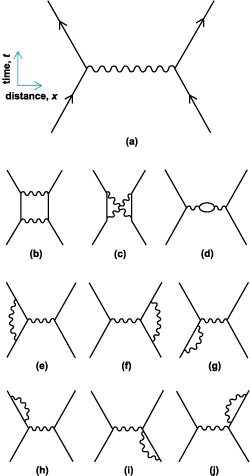
There are a lot of ways this interaction could have gone down, and each one has it's own equation (many are very similar). The diagrams help you to keep track of which one is which.
The more complicated an interaction is, the less likely it is, and the less it adds to the total probability amplitude. In the above picture:
b,c) What if two photons are exchanged instead of just one?
d) What if the exchanged photon creates a virtual electron/positron pair en route?
e,f) What if one of the electrons has a virtual photon “up in the air” during the photon exchange?
g,h,i,j) What if one of the electrons emits and reabsorbs a virtual photon right before or after the exchange?
Feynman diagrams apply to a lot more than just electromagnetic interactions. For example; neutron decay! For some reason this is the third mention of neutron decay on this website (1 and 2).
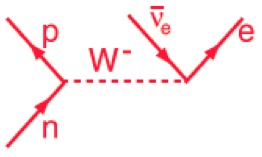
A neutron spontaneously emits a virtual W-boson which goes on to turn into an electron and anti-electron neutrino.
Unfortunately, if you really want to learn how to use Feynman diagrams you should get a BS in physics and then take several classes in quantum field theory in grad school. This stuff is crazy hard.







Hey, how’s that workin’ out for you?
With any luck there are some parallel versions of me that really have this stuff figured out. With a lot more luck at least one of them has figured out how to transmit that knowledge between worlds.
Not being lucky: it’s going slowly.
We haven’t heard from the mathematician in a long time. We miss him!
Me too. He’s stuck studying for an incredibly nasty test in about two weeks. He had to pick six advanced subjects, and the test will consist of standing in front of a chalkboard while cantankerous mathematicians yell detailed questions at him. Send good vibes.
vibes? you believe in that stuff?
Obviously not “vibes” in the touchy feely sense. More in the “shared cosmic universal soul sense”. You know, the one that modern quantum mechanics has proven exists, by bridging the gap between modern science and thousand year old eastern wisdom.
Pingback: Forget to post | An Australian in America
I read recently that a shape was discovered, called the amplituhedron, making these diagrams, dare I say, obsolete? How do amplituhedrons work in describing what feynnman diagrams describe less efficiently?
I’m not a physicist, I wish I would’ve been, starting calculus at home in my thirties 🙁 So I’m sorry if the question sounds silly. I still barely know what this stuff is.
Thanks for an awesome site.
In the electron scattering diagram given above for the ‘Coulomb’ interaction, what does the lowercase ‘e’ stand for at the vertices?
@Jackson
“The fundamental charge”. Electrons and protons have the same charge (just opposites) and we call that “e”.
Please explain which of Srinivasa Ramanujan’s formulas contributed to string theory and quantum field theory.
Also, please reveal my errors in “The Stepladder Proof of the Goldbach Conjecture” posted in Academia.edu. In brief, my simple, intuitive excess pairs algorithm quantifies 3 mandatory sets: prime,prime pairs = total pairs – prime composite pairs – composite,composite pairs. Anyone can comment on Academia.edu or my new blog htt219390965.wordpress.com or email to gregorymazur02@gmail.com.