Physicist: Magnetic fields are nothing more than the result of combining an electric field with the effects of relativity.
First some background. Magnetic fields were first defined in such a way that iron filings will point in the direction of (what became defined as) the field. The reason why filings point in the direction of the field is a little round about, but luckily the physics turned out pretty clean.
The magnetic field was defined so that pictures like this made sense.
Classical physics: A when a charge moves in some direction it creates a magnetic field that wraps around it. The direction of the field can be found using (one of) the “right hand rule(s)”.
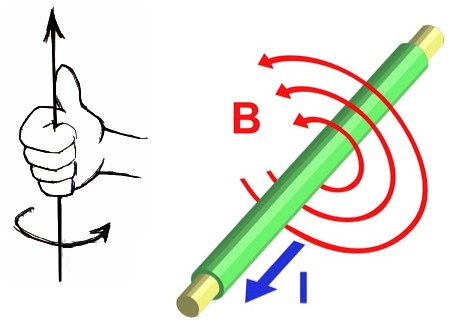
When a charge moves it's called "current". A current (even a single moving charge) produces a field that wraps around it's direction of motion according to a right hand rule: point your right thumb along the current, and your fingers will curl in the direction of the field. The greater the charge or speed, the greater the field. Physicists, being clever, generally label the magnetic field as "B" and current as "I".
In addition to creating magnetic fields, moving charges also experience force from a magnetic field that can be found using another right hand rule. Point your fingers (on your right hand, of course) in the direction the charge is moving, curl your fingers in the direction of the field, and your thumb will be pointing in the direction of the force.
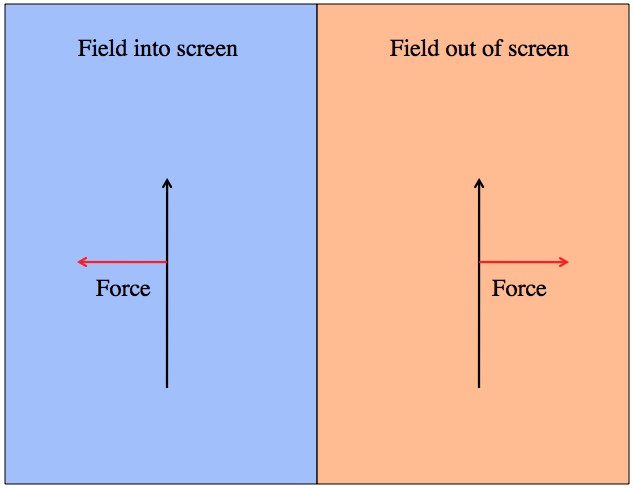
The charge is moving up. When the magnetic field points into your computer screen, the charge will feel a force pushing left. When the magnetic field points out of your screen the charge is pushed to the right.
By carefully twisting your hand about you should be able to figure out that two like charges, traveling side by side in the same direction, will experience a magnetic attraction. Of course, likes repel (and opposites attract) so the two charges will feel an electric force repulsion. This electric repulsion is always greater than the magnetic attraction, so the particles still fly apart, just slower.
The exception is things like electrical wires. There’s an equal amount of positive and negative charge in the wires, so the magnetic force is all that’s left.
But this all begs the question; how fast do the particles have to be moving so that the magnetic field they generate to pull them together is strong enough to balance the electric force pushing them apart? The answer is exactly the speed of light (not a coincidence).
Also, if wires with current in them experience magnetic forces, but not electric forces, doesn’t that make magnetic fields “real”? Not quite.
Relativistic physics: Consider the two particles flying along. If you’re moving with them, then they’re sitting still from you’re point of view, and they just fly apart (stationary charges don’t generate a magnetic field). But (classically) if the charges are moving past you they generate a magnetic field, and that keeps them from flying apart quite as fast.
However, if you write down how much time dilation the charges will experience from moving past you, the slowness of their separation is explained away. The “magnetic field” is just an illusion created by the slowing of time.
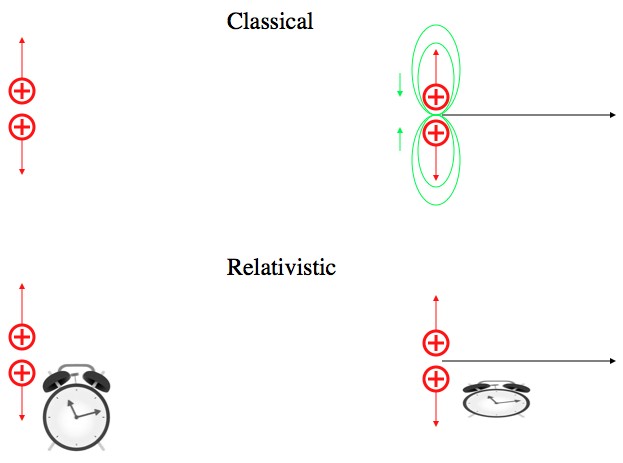
Classically, two charges moving in the same direction will fly apart slower than normal because of their magnetic field. Relativity shows that this effect is more correctly explained using time dilation: they move through time slower, so they fly apart slower.
From this point of view it makes perfect sense that in order to arrest the repulsion of the two charges, they would need to be moving at the speed of light. Like charges repel, period. So, in order to not fly apart, they must not experience any time at all (no time passes at light speed).
Now consider two parallel, current carrying wires. When current is flowing electrons (negative charge) are moving through the wire, and the protons (positive charge) in the nuclei of the atoms stay where they are. The protons see the protons in the other wire normally, but since the electrons in the other wire are moving, the protons see the electrons as closer together because of a relativistic effect called “length contraction“. The electrons, in turn, see the protons as moving and so experience the same effect. The end result is that every particle in both wires sees the other wire as have an opposite net charge.
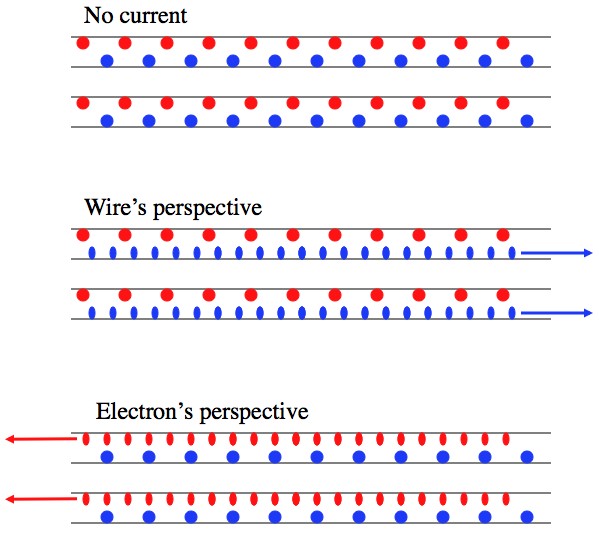
The protons in both wires see the electrons in both wires as denser due to length contraction. So they're happy in their own wire and also try to attract the other wire. The electrons experience the same thing. If the current in the wires run in opposite directions, then (for the same reasons) the wires repel each other.
So if magnetic fields are just weird relativistic effects, then where do magnetic poles, bar magnets, and whatnot come from?
So far we’ve got that current flowing in the same direction down two wires makes those wires attract, and current flowing in opposite directions makes them repel. To get the magnets of your childhood (some of our childhoods) all you have to do is turn that wire into a loop.
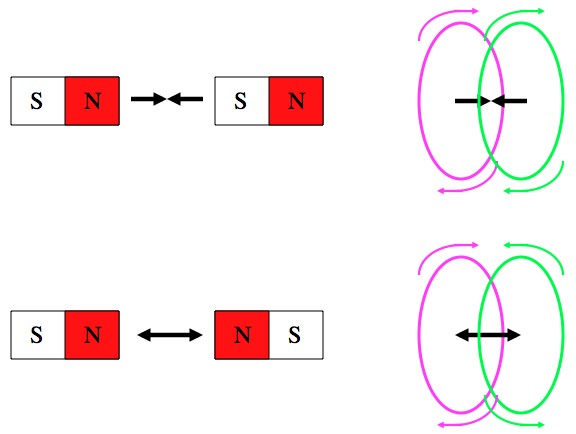
A loop of wire behaves like a bar magnet. When two are oriented the same way they attract, and when oriented oppositely they repel.
This perspective, that all magnetic dipoles (bar magnets, big and small) are reducible to current loops, helps explain a lot of things; like why there are no magnetic monopoles, and why atoms generate magnetic fields (an orbiting electron is essentially a current loop).
The more common view of the magnetic field (among physicists) is that it is merely part of a larger structure called an “electromagnetic field”. Funny story: when Einstein first wrote his big-shit paper about relativity the whole “time and space” thing was more of a side note. What he was really interested in was combining the electric and magnetic forces under one roof. In a nutshell, if a charge is moving through space in the presence of a magnetic field, it feels a push in a new direction dictated by the right hand rule (above). If a charge is moving through time, in the presence of an electric field it also feels a push in a new direction (generally to or away from another charge). So electric fields work on charges moving through time, and magnetic fields work on charges moving through space. Special relativity shows that the distinction between time and space are academic (Without batting an eye a physicist will say things like “north and east and future are three orthogonal directions”). So the electromagnetic field is just a more compact way of dealing with the two fields all at once.
Personally, I find that when you consider the source of a magnetic field (moving charges), combining relativity with the Coulomb force explains everything you need. Albeit, not very clearly, or succinctly. The rules about conservation of magnetic field lines, for example, fall out of conservation of charge and momentum. But most people would rather just work with the (illusionary) magnetic field lines than go back to basics every five minutes. And why not? It makes the math much easier.
It is a dirty secret of the popular physics literature that there isn’t a simple “F*cking Magnets, How Do They Work?” explanation in terms of quantum electrodynamics with electron-photon interactions. This is true of Feynman’s outstanding QED, as well as Brian Greene’s, Lisa Randall’s, and just about every other popular physics book.
There are in these books beautifully clear explanations of the electrostatic force using simple Feynman diagrams (as you provide here), and general relativity using the example of a spinning disk, but no comparable explanation of f*cking magnets. And no, Wikipedia doesn’t have one either.
If I’m wrong, please tell me “UR RONG!1” with a pointer to a book that explains magnets in basic terms using Feynman path diagrams, the way Feynman should have done in his wonderful QED. Or please, please write one for us yourself that doesn’t use the traditional, classical hand-waving that comes from Maxwell’s equations.
The outline of the story goes something like a Feynman diagram for electrostatics with moving frames, but that hand-waving doesn’t get at the intuitive heart of why QED should imply basic magnetic properties like polarity, the right-hand-rule, and electron spin.
I wish I could help more, but hand-waving is all I really have.
I only discovered just last week that neodymium is a lanthanide.
Elements juxtaposed are extremely radioactive.
Could this be a clue?
I’m thinking there’s something going on with the geometry of the elements that we are missing.
Pingback: QFT für alle: Relativistische Tricksereien [Hier wohnen Drachen] | Hirnspunk
Indeed, the thing I have been looking for in over 20 years of libraries and archives, study books and writings of the best physicists was exactly this: please explain me the steps from QED applied to a bar magnet to the description of the magnetic field created by it. Unfortunately I never found a clue anywhere. It seems to be harder to explain this then to find the Higgs. Personally I’m more or less convinced that this explanation in terms of “the way of QED will bring you the light” is not totally correct. Anyway, without wandering off in my own ideas on how/what I think it’s indeed a well known “secret” of physics that upto now no one has ever explained it. It would be worth a Nobel Prize perhaps for the first one to do it 🙂
http://www.archive.org/details/WhatIsAMagneticFieldRev.April22010
What a lovely explanation of relativity, you have a gift there.
And you shouldn’t excuse it as hand waving. It’s not, it’s trying to understand how relativity’s equations and ‘reality’ fit together. And doing it through relativity is like peeking through the curtains of the normal world, to see what hides behind. I like the way you think there.
You’re very kind. Thanks!
Suppose we create a magnet by using a soft-iron yoke in U shape with a coil wound around it at the middle (bend) part and the ends bend such that we get a nice homogeneous magnetic field between them. The coil itself with the currents inside is well apart from the yoke ends. How would you explain the deflection of an electron in that magnetic field? You can’t refer to the electronic current in the coil here, locally there is just the “magnetic field region” and the moving electron.
A magnetic field “flows” through metal by inducing the electrons in each of the atoms to favor spinning in a particular way (“spin” here means intrinsic spin). You can model this in terms of tiny current loops, and it’s these that you can picture when thinking about how a moving charge will get pushed around as it passes between the ends of the U.
If relativity explains the attraction/repulsion of current carrying wires then why
is there no magnetic force on a stationary charge next to a current carrying wire.
The stationary charge sees moving electrons and stationary protons in the wire
thus using the relativity argument there should be a net force on the stationary charge.
Excellent point!
There is a small attractive force.
a book i have describes the direction magnetic field at a point as the direction of the resultant force acting on a hypothetical north pole at that point.
Also, it stated-the magnetic field lines are the lines drawn in a magnetic field along which a north magnetic pole would move…
can someone explain the aforementioned?
It’s trying to describe the magnetic field in a way analogous to the electric field. That is, an electric charge is pushed and pulled along electric field lines.
This description is a little abstract because you can never actually get a magnetic pole by itself.
could you please define the dirction of a magnetic field at a point in a clear way? nothing abstract
If you put a compass at that point, the needle would point in the direction of the field.
do perpetual magnetic generators work? i need to make one for a project. what if i take two circular disks and stick circular magnets along its’ edges .in both disks the poles placed outward would be alternate..i.e: one north and one south outward.. now i fix the disks in a manner such that surfaces of the disk with the magnets face each other .I connect multiple copper wire loops together forming a circle,and now place this between the 2 disks…after giving the first push to one of the disks,would the disks continue to rotate due attraction and repulsion?
how can i arrange the magnets in farraday array?
Pingback: QFT für alle: Relativistische Tricksereien – Hier wohnen Drachen
Can you use these relativistic concepts to explain inductors? Specifically how is a magnetic field “built up” and how does the collapse of the magnetic field in an inductor produce a current?
Pingback: Personalidad magnética | Tópicos Químicos
Curio asked “why is there no magnetic force on a stationary charge next to a current carrying wire.” I think the electron would orientate itself in a particular direction due to its magnetic moment, but I do not think Faraday would agree with your comment “There is a small attractive force”, as an electric force is the result of a changing magnetic field, and for a stationary charge along side a wire with a steady current the magnetic field is constant.
Although physicists can clearly predict magnetic effects; as people have commented above, physicists really do not understand magnetism. It is just a shame they cannot admit it.
Of course a stationary charge placed beside a wire with no current, will feel a small attractive force, due to inducing an opposite charge on the wire. This would presumably also be true when a current is flowing, but I not sure if it would be the same strength.
What has a Physicist to say about the work done on a particle => Force × the distance it moved in relation to a magnet? The Magnet is not moving still it will hang on a refrigerator for 20 or many more years. It delivers work and Force but how about the moving part???
There is no such thing as a static in this universe. Everything is in motion, its just that some motions appear static because they are repetitive or being looked at from a macroscopic viewpoint. As to the work done in the refrigerator magnet, from a macroscopic viewpoint, there is no motion, therefore no work done. From a nanoscopic viewpoint, the work is give and take with a net zero result on time-scales much greater than the frequencies involved.
I have an even more difficult problem with the magnetic field (and electrostatic and gravitational fields as well). Here’s the thing: In all other forces, something physical is going on. In a simple lever, the lever transfers physical force from the lever presser to the object being moved. In steam power, molecules of superheated water push against a piston. Similarly, in an internal combustion engine, superheated molecules of fuel push against a piston. In fission and fusion bombs, particles are pushing etc. All of these involve physical entities. But a field can (and does) exist in a vacuum, and the force exerted by the field works its magic by…what? Where and how do fields exert physical force on matter? What, without arm waving and blowing smoke, goes on there?
I am not sure anyway completely understands what a magnetic field or electric field is. Mathematically, the electric and magnetic fields can be derived from an electric potential field and a magnetic vector potential field, which can themselves be derived from a single scalar field. We cannot directly observe changes in these higher-level fields, however, and they can have an arbitrary constant added to them without changing the magnetic and electric fields that derive from them. BUT they still do appear to have some effects. It appears, though it is not entirely certain yet, that the Arhanov-Bohm effect is caused by the Magnetic Vector Potential outside of any measurable electric or magnetic fields. I believe it is fairly likely that if we were to study the highest level of these fields, we would find other effects that are missing when looking solely at magnetic and electric fields. Perhaps a source of gravity could be found there. Also, it would seem most if not all of quantum mechanics can be derived from stochastic electrodynamics, which applies classical laws to a large amount of small, random background energy. It could well be that small changes in the background energy cause the effects we interpret as relativity, magnetic and electric fields etc. I have seen such a formulation where the wave forms of matter are distorted in ways that cause the effects of relativity. Wave mechanics can also account for quantization and the indeterminancy of inter-related quantum measures, because the same thing is easily demonstrated to occur when measuring waves.
Pingback: Magnet painting art | IDEA Studio 2 | Creative Robotics
Pingback: Magnet painting art – FINAL DOCUMENTATION | IDEA Studio 2 | Creative Robotics
I think that saying it’s just coulombs law and relativity is begging the question a bit.
I would suggest to you instead, that it’s coulombs law and constancy that changes to the electric field propagate at; and that relativity is a consequence of that.
The thing that got me for a while was why a charge moving next to a neutrally charged wire carrying current; why that charge curves.
Clearly, if magnetic fields aren’t ‘real’, then what curves the charge?
The answer I found is that it’s not that magnetic fields aren’t ‘real’ it’s just that magnetic fields are just the angular momentum of the electric field.
What happens is that as each charge moves along the wire; the electric field ‘spins’ around the outside of the wire, radially in and out. But, subtly, it’s not that that spin *generates* the magnetic field- that spin IS the magnetic field!!!
If you integrate up the effect of that spinning electric field, you find that a free charge outside the wire moves because of it, in the way you would expect because of the ‘imaginary’ magnetic field. And the effect of each moving charge in the wire adds together giving the ‘magnetic field’ that we perceive.
So it’s roughly analogous to linear angular momentum; there’s not two different momentums, linear momentum essentially implies the existence of angular momentum. Likewise there’s not electric field and magnetic fields, there’s just electric fields that propagate at a fixed speed.
According to QED, electric charges are made up of clouds of virtual photons. If magnetic fields are just electric fields, then they too should be clouds of photons.
I know I am a late comer but just for future reference:
>”So if magnetic fields are just weird relativistic effects, then where do magnetic poles, bar magnets, and whatnot come from?”
If by this, you mean that, in a reference frame in which the Maxwell equations say the B field is nonzero, you can just ignore B and account for all the observable effects using the E field alone together with length contraction, etc., then this is, of course, WRONG!
Also it may not be always possible to (Lorentz) transform to another frame, in which B is made zero; Because such a transformation is a global one.
There is a very subtle sense in which the B field is a implication of a moving E field, but all of those aspects cannot be captured using simple length contraction with E (In fact, it’s Maxwell’s B field which accounts for all those effects of a moving E, ironically).