Physicist: They definitely both experience time dilation. That is to say, they both see the other person moving through time slower (you will always see your own clock running normally, in all circumstances). The short resolution to the “paradox” is: if you’re flying past each other, and never come back to the same place again to compare clocks, what’s the problem? You may both observe the other person’s clock running slower, but that’s not a contradiction in any “physical sense”.
Of course if you do meet up again, then you’ve got the “twin paradox”, which still isn’t a problem (or a paradox). One of the most frustrating things about the universe is that there is no such thing as “absolute time“, which would allow you to say “who’s right”. If you could ask the universe “what time is it?” the universe’s best answer would be “that depends on who’s asking”. The universe is kind of a smart ass.
There’s a halfway decent explanation of the twin paradox here: “Q: How does the twin paradox work?” and there’s a quarterway decent, possibly simpler, explanation of why movement makes time pass slower here: “Q: Why does going fast or being lower make time slow down?“. Personally, I think the question of this post is far more profound.
I should note here that the language physicists use makes the situation sound subjective; “the observer sees…”, “the person experiences…”, etc. However, none of the effects (covered in a minute) are due to observer based effects, like the delay caused by the time it takes light to get from place to place. Everything here is literal and physically real.
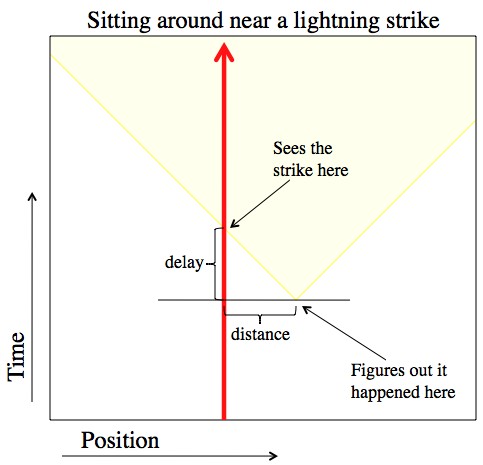
You don’t see an event when it happens, you see it when the light from the event gets to you. But you can easily figure out when it did happen by dividing the distance to the event by C, giving you the time delay.
This diagram is pretty standard physicist fare. If you want to draw a picture of something happening in 4 dimensional spacetime, you just drop two of the spacial dimensions. So here, time is up, space is left/right, the red arrow is a person (it doesn’t have to be a person) sitting still and moving forward in time (like you’re doing right now, in all likelihood). The yellow triangle is a lightning strike (at the bottom) and the light expanding out from it. The picture should make sense; the longer after the lightning strike (the higher on the picture) the farther the light from the strike has traveled (wider to the left and right). “Lightning” is a common example of an event, because it hits in a definite place at a very definite time. Plus, (spoiler alert) lightning is bright so, unlike most small instantaneous things, it makes sense that everyone should be able to see them.
Now let’s say you’ve got two people; Alice, who likes to hang out by the train tracks, and Bob, who likes to ride trains on said tracks.
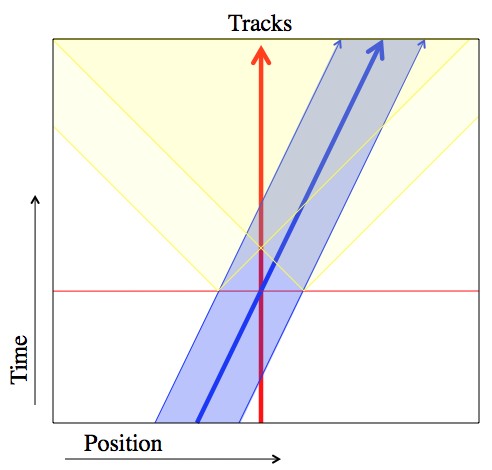
A train car (light blue) moves to the right. Right when Alice and Bob are eye-to-eye the front and back of the train car are hit by lightning. This moment, that Alice calls “Now!”, is the red line.
As the train, with Bob sitting in the exact center, passes Alice they high-five each other. Suddenly, both ends of the train are struck by lightning. Alice knows this because, very soon after the lightning strikes, the light from them get to her. Being smart, she realizes that the strikes must have happened at the same time, because they happened equally far away from her, and the light took the same amount of time to get to her (see picture). Moreover, really milking her cleverness, she predicts that Bob will see the lightning bolt at the front of the train first, and the lightning bolt at the back of the train second (see picture, some more).
The speed of light, C, is an absolute. No matter where you are, or how fast you’re moving, C stays exactly the same. So Alice’s reasoning is completely solid, and she’s right when she says that the lightning bolts happened at the same time.
When you say that two things are “happening at the same moment”, or “happening now” you’re saying that they’re on the same spacetime plane, that I’ll call a “moment plane”. In the same way that a regular 2D plane is a big, flat subset of regular 3D space, the moment planes are big flat 3D subsets of 4D spacetime.
So the high five, the lightning strikes, and everything else in the universe at that moment, are all in the same “moment plane”. However, that doesn’t necessarily mean that everything in that plane happens at the same time (although they do for someone, in this case Alice).
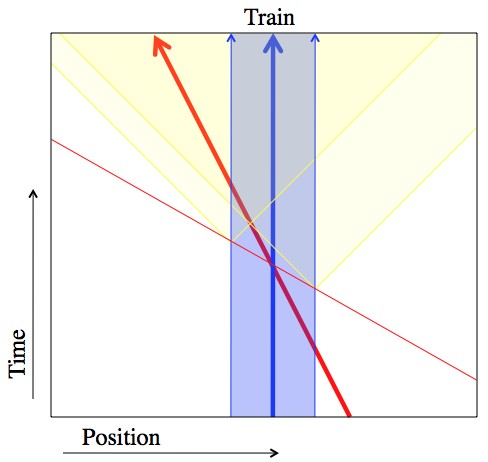
Same situation from the perspective of the train. Bob sees the lightning at the front of the train first, and the lightning at the back of the train second, and can even figure out that Alice will see them at the same time. However, he disagrees with Alice about when things happen.
Around 1900 the Michelson Morley experiment (among others) was demonstrating that the speed of light seemed to be the same to everyone, regardless of whether or not they’re moving. Einstein’s great insight was “Hey everybody, if the speed of light seems to be the same regardless of the observers’ movement, then maybe it really is?” He was a staggering genius. Also, he was exactly right.
So, Alice was right about Bob seeing the front bolt first, and the back bolt second. However, as far as Bob’s concerned, she was wrong about why. Using the same reasoning Alice did, he figures that the speed of light is fixed (whether or not you’re moving), and the distance from him to the front and back of the train is the same, so since he saw the front bolt before the back, it must have happened first. And he’s right. Moreover, he thinks that the reason that Alice saw both at the same time is that she’s moving to the left, away from the first bolt and toward the second (picture).
The first thing that most people say when the hear about the train thought experiment is “Isn’t the person on the tracks correct, since they really are sitting still?” Nope! The tracks may be bigger, but (as Dr. V. E. Kilmer discovered experimentally) there’s no physical way to say who’s moving and who’s not.
Both Alice and Bob are completely correct. What’s very strange is that the ideas we intuitively have about “nowness” are wrong. As soon as two people are moving with respect to each other, the set of points that they consider “now” are no longer the same (different moment planes). Alice’s “now” is the same red line above, but Bob’s sees it as “tilted”.
After all of that, what you should take away is: “a thing’s moment planes tilt up in the direction of its movement” (picture above). If this is the first time you’ve seen this sort of stuff, you shouldn’t really believe any of it. Or at least, you shouldn’t have internalized it.
This stuff isn’t terribly complicated, but it is really mind-bending, so take a moment.

Physically tilted “nows” are difficult to wrap your mind around. To encourage the reader to pause or go back a little bit; consider the above.
Finally, to actually answer the question, imagine the situation from the point of view of someone in between Alice and Bob, who sees them flying off at equal speeds in opposite directions. This puts Alice and Bob on equal footing, and there’s no questions about “who’s right” or “who’s moving”.
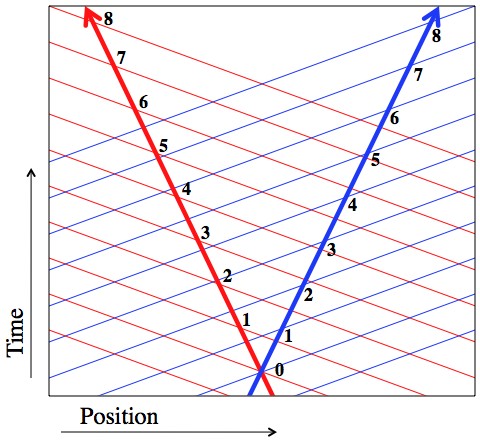
Alice and Bob’s now planes at various times. If you were to ask Alice “how much time has passed for Bob now?” the answer will always be “less time than for Alice.” The situation with Bob is exactly symmetrical.
Since the moment planes of each person “tilt up in the direction of movement”, each person is always trailing behind the other in time. When they pass each other they each start their stopwatches. For that one moment they can agree that T=0 for both of them. But that’s where the agreement ends. If you ask Bob about what set of points in the universe (both position and time) correspond to T=7, he’ll have no trouble telling you. Specifically, he’ll tell you “right now my stopwatch reads ‘T=7’ and, F.Y.I., Alice’s stopwatch reads ‘T=5′”. Bob recognizes that this is because her clock is running slower, and he’s right. At least, he’s right in terms of how time is flowing for him.
If you were to run over to Alice at the moment that her stop watch reads 5 (using a TARDIS or something), she would say “right now my stopwatch reads ‘T=5’ and Bob’s reads ‘T=3.5′”. Also being clever, she realizes that this is because Bob’s clock is running slower, and she’s right. Notice she doesn’t say “T=7”. Once again, this is because they disagree on what “now” means, since their moment planes aren’t the same.
The first question that should be coming to mind is something like “Well, what’s really happening?” or “How is time actually passing?”. Sadly, time is a strictly local phenomena. How it flows is determined (defined really) by relative position and relative velocity. That is to say, there is no “universal clock” that describes how time passes overall. The only reason that there seems to be some kind of universal clock is that we (people) are all moving at very nearly the same speed. Or equivalently, we’re all sitting still in very much the same way. Our time, length, and speed scale are all just too small.







Well answered!
One thing I couldn’t get my head around was how the second to last paragraph was worded. How far off base am I by thinking that Alice wouldn’t say that _Bob’s_ stopwatch read 3.5, she’d say that from *her point of view* a stopwatch on that train has only counted 3.5.
Because Alice, being clever, possibly knew that Bob’s actual stopwatch would be reading a greater time than that on her own?
Got here from a comment on New Scientist, and your explanations are thoroughly clear and enjoyable. Cheers!
Her, and everyone else in the universe who’s sitting still with respect to her.
That may have been a better way to write it, but I was trying to avoid using the phrase “from so-and-so’s point of view”, since it implies (maybe not directly) that the effect is a little illusionary.
If you were moving like Alice (and so have the same moment planes) but happened to be where Bob is at T=5, then you could read his stopwatch directly, and it would definitely read 3.5.
You would view eachother as the people on earth moving at normal speeds see you. Time dilation changes/effects you/youre situation alone. And others see a virtually altered image so you don’t seem to be breaking the laws of physics. And if you could break these laws and travel at the speed of light, you then step into a deferent dimension or space or something, it could co exist hear in our universe or temporarily transport you elswere persay because you and you’re physical space begins to use different physics in that specific localized area you occupy (yet to people on earth you are still using there physics).
Sound legit? What I’m saying is not wrong, just may be incomplete and need better explaining.
If you’re interested in this, check out my Relativity and FTL Travel FAQ at
http://www.physicsguy.com/ftl/
Chapter 2 (http://www.physicsguy.com/ftl/html/FTL_part1.html#chap:spacetime) describes space-time diagrams–what they mean and how they are constructed. Section 4.2 (http://www.physicsguy.com/ftl/html/FTL_part2.html#sec:twin) uses space-time diagrams to explain the Twin Paradox–part of which asks “how can each twin think the other twin’s clock is running slowly.”
Pingback: Q: Why does relativistic length contraction (Lorentz contraction) happen? « Ask a Mathematician / Ask a Physicist
In my greatest opinion I think what it all comes down to is a real life setting.
If you don’t have anything to begin with than you have nothing to power (multiply).
So, in the last example, what happens if they turn around and move back towards each other? Do their times “catch-up” resynchronize once they are together again?
In other words, does time “accelerate” when the two observers are moving towards each other, just as it slows down when moving apart?
If they were moving symmetrically, then when they turned around their “now planes” would swing such that they saw the other person as farther ahead in time, but still moving through time slower. By the time they came back to the same place their clocks would read the same again.
However, if just one of them turned around to catch up to the other, or if in any other way their paths weren’t symmetrical, then their clocks would disagree when they met up again. This is much, much easier to talk about in terms of the twin paradox than tilted now planes. Just a right tool for the right job sort of thing.
so from bobs perspective when bobs clock reads 6, alices reads 4
and from alices perspective when her clock reads 4 bobs reads 3
in order for alice to see bobs clock at 6, hers would need be at 8
so if at the moment bobs clock read 8 (from bobs perspective) they both became stationary (relative to one another) and teleported to one another. what would their clocks read? certainly they couldnt STILL see each others clocks being behind. one would suddenly be ahead and the other not? i always thought the one moving saw outside (less moving) events happening faster then the moving persons events to compensate for the stationary person seeing the moving persons move slower…
When they’re brought back to rest with each other one could be ahead or behind the other. It’s a twin paradox thing.
When you say “come to a rest with respect to each other” that could mean Alice accelerates into Bob’s frame, or Bob accelerates into Alice’s frame, or something in between like (what you were probably thinking of) they accelerate toward each other the same amount. It matters because when you accelerate it swings your “now plane” around. For example, if Alice does all the accelerating she will come to rest with respect to Bob, and they will agree on “now”, however her clock with be behind. It’s the other way around if Bob does all the accelerating.
This same sort of problem crops up with teleportation. You can think of teleporting as moving along a now plane, but you have to ask “whose now plane?”.
Unfortunately, in the exact same way that there’s no “universal time”, there’s also no “universal stationary”. So whatever you find is true of a moving object, must be true of you from that same object’s perspective. In other words, you can’t talk about “moving” and “stationary”. The best you can do is talk about “moving with respect to each other”.
so its the acceleration then, that accounts for the time difference when they enter each others frame? but the difference in constant speed that makes the others time appear to be moving more slowly? and the acceleration isint relativistic as the speed is? i mean, only one is accelerating and not the other? but cant the same argument be made that from each point of view the other is accelerating and not the one looking? sorry, just trying to wrap my mind around this.
its seems with that explanation, if i accelerated to near the speed of light, then flew around for a year at constant speed, then came to rest at earth that i would experience just as much time shift as i would have if i flew around for 10 years at a constant speed instead of one year.
This is a subtle point, and it bothers a lot of people. It’s not so much that the acceleration itself has any effect, so much as any circuitous route is going to involve some acceleration.
And, backward as it sounds, the more round-about a path through spacetime is, the less time it experiences.
In a nutshell, the person who never accelerates travels in a straight line. The person who does accelerate follows a bend line and a longer path. Longer path = less time (strange as that sounds).
There’s a post that goes into needless detail here.
The “length” of a trip in spacetime is defined by the “spacetime interval”, which takes into account both distance traveled and time taken. The spacetime interval of a path is equal to the amount of time experienced by whatever follows that path and, oddly enough, gets shorter the more turn corners. It violates the “triangle inequality“.
Pingback: Q: Hyperspace, warp drives, and faster than light travel: why not? | Ask a Mathematician / Ask a Physicist
(Reposted due to an error?)
A Planck unit of time is about 5.4 x 10^-44 of a second. Philosophers (including me) assert that reality unfolds one Planck frame at a time.
In my blog post A Subjective View of Time, I calculated that if you walk away from me at a speed of one metre per second for only one second then you will have changed your time frame relative to me by more than 10^26 Planck units by virtue of the time dilation effect! In other words you will be in a different reality to the one you left one second ago.
If you raise your arm, your finger tips will have moved into a different time frame at the Planck scale. In fact every part of your arm will be in a different reality to every other part according to its differing speed and time of travel. Ludicrous? Suppposedly so!
This tells me that either time does not really exist or it is a conscious construct. If neither of the above then theres something really wierd about the relationship of time to reality.
As an avid Star Trek fan this poses some awkward questions about “real-time” sub-space communications when travelling at warp speed 🙁
Wonderfully clear explanation! Thank you! So, time is not a constant. This makes me wonder what time is, really. I think I will look for/ask a new question. This site is so awesome!
Pingback: Q: How does instantaneous communication violate causality? | Ask a Mathematician / Ask a Physicist
Pingback: Q: Is it possible to experience different rates of time? If time were to speed up, slow down, or stop, what would you experience? | Ask a Mathematician / Ask a Physicist
Pingback: Q: Do the past and future exist? If they do, is the future determined and what does that mean for quantum randomness? | Ask a Mathematician / Ask a Physicist
There’s one thing I don’t understand. It’s about Alice’s deduction that Bob will experience the lightning bolt hitting the front of the train first. She comes to this conclusion because, to put it one way, bob is moving toward the light emitted from the front strike. So he will encounter the light from the front strike first. But doesn’t Bob, being clever, know this?
I’ll use a more simplified example (in that it excludes alice). A spaceship is halfway between our sun and Alpha Centauri, moving at a constant speed. At one particular moment, a radio wave is sent from the sun and another sent from Alpha Centauri such that the waves themselves would encounter each other at the halfway point (i don’t really know how to put this for relativity. they meet in the middle, they are constantly equidistant, you know what I mean. If the ship were stationary it would receive both signals at the same moment) Now if the ship is traveling towards the Sun it will encounter the sun’s wave first, and later encounter the second wave from Alpha Centauri. Or the other way around if it were traveling toward Alpha Centauri. But an intelligent pilot traveling in the sun’s direction wouldn’t assume that the sun sent it’s wave first. the pilot would know that it was also moving toward the sun’s wave, and away from Alpha Centauri’s wave. Couldn’t the pilot deduce that the waves were sent at the same time? Is that question meaningless because there is always some reference frame from which it appears the two waves are sent at the same time?
…so if a person left earth on a 10 lyr voyage, rolling a constant 0.5c (feels galactic scenery blow by him at 0.5c) through the cosmos, charting a circle and ending up at earth again… Would an observer on earth chart his velocity as a parabola? 0.5c away slows and then 0.5c towards?
I understood till the point “she predicts that Bob will see the lightning bolt at the front of the train first, and the lightning bolt at the back of the train second” and bob saying “the distance from him to the front and back of the train is the same, so since he saw the front bolt before the back, it must have happened first”. But according to special relativity if there is a time dilation there is length contraction too. Alice should see train contracts because train is moving with respect to Alice. If so, Alice should see that light strike reaches bob even before she expected. Doest mean Bob has seen an event something that didnt happened yet?
I have a question. Do some space-like separated events become time-like separated due to lenght contraction?
@Vlad
That’s one of the reasons why that distinction is made; each of the different types of separation (spacelike, timelike, and lightlike) stay the same regardless of the reference frame. No matter how much length contracts or time dilates, spacelike separated events stay spacelike.
I did not manage to understand almost anything. The wording proved impossible to make sense of, which frustrated me greatly.
As an aside to this critique, I’d like to say that I thought Bob would see the front strike first because he was moving towards it, and the rear strike second because he was moving away from it. Thus, the light from the rear strike has “catching up” to do, and it takes longer to reach him. And I also thought there was objective truth because if I were to unleash the strikes simultaneously with the press of a button in my and Alice’s frame of reference (standing still on the Earth – yes I know it’s moving, or everything else is moving and the Earth is standing still, whatever, irrelevant), Bob would still maintain that the front strike happened first, but he would, in fact, be wrong. The strikes occured simultaneously, because I triggered them and they were programmed to go off at the same time (in our thought experiment). This reasoning, and its conclusions, are incorrect, right?
So obviously I’m way off here, but I have not gained any insight whatsoever from this article. I am still completely baffled by time and spacetime.
As another aside, the many worlds theory sounds like the most preposterous jibberish I have yet encountered. I am with Einstein and his hidden variables. Btw, what exactly is the mechanism that produces the variations in all these purported worlds? What generates variables?
So it’s not the naive “Alice is sitting still” argument that baffles me – I understand the relativity when it comes to movement. What seems important to me, however, is who is moving relative to the events we are measuring. Is it not the case that Alice indeed is not moving relative to the bolts of lightning, despite Bob’s thinking she is heading towards the rear bolt – and thus seeing it first? Because he is obviously wrong there, as she sees the light from both strikes at the same time. He, however, does not, as he indeed is moving towards the front bolt, and away from the rear one.
So it is movement relative to the “event” measured that strikes me as important. Perhaps I’m missing something here, it is quite late in the night…
If the “front” bolt was produced by a device installed on the front wagon, would it not change everything? Alice would say the front one occurred after the last one, and Bob would say the opposite. And they would both be wrong, as the strikes would’ve occurred at the same time (again).
Please elaborate kind sir.
Or would Alice still say they both occurred at the same time? The light would move irrespective of the train after all.
Pingback: Q: Since the Earth is spinning and orbiting and whatnot, are we experiencing time wrong because of time dilation? | Ask a Mathematician / Ask a Physicist
suppose person B was standing with person A at some point O and now person B starts to move with velocity c/2 w.r.t A on a straight track(starting from O) and both the observors(A and B) start to note time on their identical clocks attached to their respective frames .Now after 1 second (according to A’s clock) person B is made to stop suddenly(by applying huge amount of force that means assuming that its velocity suddenly drops to zero from c/2). therefore distance b/w A and B according to A must be = c/2(m/s) * 1s=c/2 m. but according to B’s clock time just before he was made to stop as shown by his clock was “gamma*1(sec)”.and therefore distance b/w(A and B) them according to B must be =c/2(m/s)*gamma(s)=c/2*gamma.
now who is correct or is there anything wrong in the question …i’m not getting..please help
Isn’t the answer to the question when the bolt strikes happened dependent on their own frames of reference with respect to each other? If you put two people on the spots where the lightning strikes occured, they would be hit at the same time? So who cares what Bob sees? It’s because he uses light to judge when stuff happens? It seems to me it’s completely irrelevant what they think happened at the same time.
Could two people see each other from two different planets
Question: would it be possible for two people to disagree about whether an event has even happened yet?
Let’s say we have two people (let’s use Alice and Bob), a photon emitter, and a photon detector a fair distance away. Alice stands next to the photon emitter, the detector is a fair distance away (far enough to make the effect I describe below happen), and Bob is behind the emitter some distance.
At the instant Bob sees the photon emitter shoot a photon toward the detector, he starts moving toward it at 0.99c. Gamma gives that the factor of length contraction for him would be about 200, meaning that the photon has to travel a mere 1/200th of the distance to the detector from Bob’s point of view as it does from Alice’s. Let’s say this is short enough for the photon, which has constant speed from both perspectives, to hit the detector and for him to see that the detector has gone off, but Alice hasn’t seen this from her perspective yet, since the photon has to travel a much longer distance.
So Bob stops when he reaches Alice. He’s seen the photon reach the detector, but Alice hasn’t, and they communicate this to each other. But the thing is, now they disagree about the ORDER of events (them talking vs. the detector going off), which IIRC doesn’t work. The question I have is: what exactly is wrong with the scenario? There has to be something, but I can’t figure out what.
I just was looking for an article to explain why me and my girlfriend both saw my hand trail at the same time. I was looking at my thumb trail and then she asked if I saw it too. I thought it was something just do do with my own vision but I found it odd we both saw it. Any explanations?
Pingback: Q: In relativity, how do you define “the observer”? | Ask a Mathematician / Ask a Physicist
So what effect of space expansion could account for our planet to experience ~10,000 years since its creation while the observable universe experience 13 billions of years since creation?
Hi. Is the short story that nothing can happen at the same time if it doesnt happen in the same space?
@Joggi
Just about. Things can’t happen at the same time, from all perspectives, unless they happen in the same place. It’s a little like saying that two things can be side-by-side from all perspectives unless they’re in the same place, because if they’re not, then side-by-side from one perspective is one-in-front-of-the-other from another perspective.
Thank you for your quick reply.
I also have a question about Alice and Bob and the trainwagon.
If we add that both Alice and Bob know that the wagon has a malfunction so that if it gets hit by lightning on both ends it will explode in a minute. Alice see the lightning strike at the same time. She calls Bob and tells him to get of the train before it explodes, but Bob tells Alice to relax, cause he saw the light hit one end of the wagon before the other. Will the train explode?
@Joggi
“Simultaneous” isn’t a thing. Like you point out, different perspectives will disagree on whether events are simultaneous or sequential. There’s no objective, universal notion of simultaneity.
So it depends on the train’s point of view and how exactly this self-destruct system is set up.
Did any of you have ever heard the story of king kakudmi from hindu religion book bhagwat puran, The book written thousands of years ago it clearly states that whenever you move out of earth to farther place the time span changes. My question is how did the rishi or sages of hindu religion has known this concept of time space relationship so long ago, of which modern day scientists are still doing research to figure it out.