Clever student:
I know!
= 
= 
= 
= 
.
Now we just plug in x=0, and we see that zero to the zero is one!
Cleverer student:
No, you’re wrong! You’re not allowed to divide by zero, which you did in the last step. This is how to do it:
= 
= 
= 
= 
which is true since anything times 0 is 0. That means that
= .
Cleverest student :
That doesn’t work either, because if 
then
is 
so your third step also involves dividing by zero which isn’t allowed! Instead, we can think about the function 
and see what happens as x>0 gets small. We have:
= 
= 
= 
= 
= 
= 
= 
= 
=
So, since = 1, that means that = 1.
High School Teacher:
Showing that approaches 1 as the positive value x gets arbitrarily close to zero does not prove that 
. The variable x having a value close to zero is different than it having a value of exactly zero. It turns out that is undefined. does not have a value.
Calculus Teacher:
For all 
, we have
.
Hence,
That is, as x gets arbitrarily close to (but remains positive), stays at .
On the other hand, for real numbers y such that 
, we have that
.
Hence,
That is, as y gets arbitrarily close to , 
stays at .
Therefore, we see that the function 
has a discontinuity at the point 
. In particular, when we approach (0,0) along the line with x=0 we get
but when we approach (0,0) along the line segment with y=0 and x>0 we get
.
Therefore, the value of 
is going to depend on the direction that we take the limit. This means that there is no way to define that will make the function 
continuous at the point .
Mathematician: Zero raised to the zero power is one. Why? Because mathematicians said so. No really, it’s true.
Let’s consider the problem of defining the function 
for positive integers y and x. There are a number of definitions that all give identical results. For example, one idea is to use for our definition:
:= 
where the y is repeated x times. In that case, when x is one, the y is repeated just one time, so we get
= 
.
However, this definition extends quite naturally from the positive integers to the non-negative integers, so that when x is zero, y is repeated zero times, giving
=
which holds for any y. Hence, when y is zero, we have
.
Look, we’ve just proved that ! But this is only for one possible definition of . What if we used another definition? For example, suppose that we decide to define as
:= 
.
In words, that means that the value of is whatever 
approaches as the real number z gets smaller and smaller approaching the value x arbitrarily closely.
[Clarification: a reader asked how it is possible that we can use in our definition of , which seems to be recursive. The reason it is okay is because we are working here only with 
, and everyone agrees about what equals in this case. Essentially, we are using the known cases to construct a function that has a value for the more difficult x=0 and y=0 case.]
Interestingly, using this definition, we would have
= 
= 
=
Hence, we would find that 
rather than . Granted, this definition we’ve just used feels rather unnatural, but it does agree with the common sense notion of what means for all positive real numbers x and y, and it does preserve continuity of the function as we approach x=0 and y=0 along a certain line.
So which of these two definitions (if either of them) is right? What is really? Well, for x>0 and y>0 we know what we mean by . But when x=0 and y=0, the formula doesn’t have an obvious meaning. The value of is going to depend on our preferred choice of definition for what we mean by that statement, and our intuition about what means for positive values is not enough to conclude what it means for zero values.
But if this is the case, then how can mathematicians claim that 
? Well, merely because it is useful to do so. Some very important formulas become less elegant to write down if we instead use 
or if we say that is undefined. For example, consider the binomial theorem, which says that:
= 
where 
means the binomial coefficients.
Now, setting a=0 on both sides and assuming 
we get
= 
= 
= 
= 
= 
where, I’ve used that 
for k>0, and that 
. Now, it so happens that the right hand side has the magical factor . Hence, if we do not use then the binomial theorem (as written) does not hold when a=0 because then does not equal .
If mathematicians were to use , or to say that is undefined, then the binomial theorem would continue to hold (in some form), though not as written above. In that case though the theorem would be more complicated because it would have to handle the special case of the term corresponding to k=0. We gain elegance and simplicity by using .
There are some further reasons why using is preferable, but they boil down to that choice being more useful than the alternative choices, leading to simpler theorems, or feeling more “natural” to mathematicians. The choice is not “right”, it is merely nice.
The upper limit of the index k in the binomial theorem is n, not infinity. But the argument still holds. Thank you for convincing me: 0^0 is NOT (or rather, should not be allowed to remain) undefined, even though it is a singularity in z = x^y.
If one insists on y^x being a continuous function, then you run into multiple answers, depending on how you take the limit. But if you drop that requirement there are many reasons to define 0^0 as 1.
It is a mistake when you write 0^0=0^1. 0^{x-1} because 0^{x-1} don’t exist if x<1.
Most scholar mathematician:- By laws of indices, the high school teacher is right.
a^0=a^m/a^m which is 1 for (a,m)>1. But 0^0=0, for which the answer terms down to 0/0 which is not defined or imdetermined.
All of these could be possible for “anything” to the zero power is one. However, zero times itself is still zero. The question remains. Is this one, or zero? I believe that it is a problem that can not be solved in our particular dimension. Yet, in the fourth dimension it could be solvable because of it’s the warped structure making other numbers possible.
Very interesting.
Thank you professor.
Pascal says:
(a+b)^n= Σ(i=0:n) nCi a^i b^(n-i)
Example 1:
(1+2)^3=
1•1^0•2^3+
3•1^1•2^2+
3•1^2•2^1+
1•1^3•2^0
= 8+12+6+1 = 27
Example 2 (“proof” that 0^0 is 1):
(0+1)^2=
1•0^0•1^2+
2•0^1•1^1+
1•0^2•1^0
= (0^0) = 1
The binomial formula nails down the answer.
Most directly:
1 =
(0+1)^1 =
Σ(i=0:1) 1!/(i!(1-i)!) • 0^i•1^(1-i) =
1•0^0•1^1 + 1•0^1•1^0
= 0^0
Q.E.D.
The answer can be demonstrated quite simply and it is undefined:
Consider:
x^0 = x^1 * x^-1
When we set x to 0, the equation becomes:
0^0 = 0 * (1/0) = undefined
As we know 1/0 is undefined, then we know that 0^0 is undefined.
Your first equation is not valid for x = 0, but you use it as if it is. So this does not prove anything.
This “problem” is of the same type (though a little more involved) as determining 0! (zero factorial).
Given the natural definition for n-factorial (all natural numbers multiplied together up to n) and natural definition of a^n (a multiplied by itself n times), neither 0! nor 0^0 has any true conceptual meaning. They are mathematical objects of the mind that pop out because of our algebraic fiddling – that is to say, our use of notation.
A good example of this is the first term of the Taylor Series for e^x.
e^x = 1 + x + x^2/2 + x^3/6 + x^4/24 + …
We choose for notational convenience to rewrite this as
e^x = Σ(k=0:inf) [ x^k / k! ]
Now, looking carefully at the first term of our infinite sum, we find we have x^0 / 0!
Now, this first term equals 1. It equaled 1 before we chose to use infinite sum notation to represent it. Given that the first term in the Taylor Series is 1, and our convenient notation pops out x^0/0!, we must decide quickly that 0! must equal 1 to preserve the notation.
Now, what is e^0. Before we started using our summation notation, we knew it to equal 1. Now, for x=0, our convenient summation notation gives us a first term of 0^0/0!
Now we need to accept 0^0 = 1 to preserve out notation.
The only alternative here is to go back and rewrite our Taylor Series as
e^x = 1 + Σ(k=1:inf) [ x^k / k! ]
Neither 0^0 nor 0! have any sensible “meaning” related to our natural definitions of powers and factorials, but for the convenience of our most algebraically useful notation, we choose to say 0!=1 and 0^0 =1. We accept these values and carry on.
use polynom 0°= 1
HK nailed it, both conceptually and formally.. we accept as a matter of definition that 0! = 1. Why is there any controversy that 0^0 = 1 as well? I think it’s because we think about 0*0 as a factor of 0^0, and trust intuition.
Fatih, what are you talking about? It sounds like you’re regarding a function polynom() in some math toolkit as the ultimate authority on math theory. (“Just google it!”) Or…?
No,all the answers are wrong.
The answer is undefined.
Actually 0^0 is one of the indeterminate forms according to limits.
If f(x)=0,g(x)=0. Lt x tends to a f(x)^g(x)=e^Lt tends to a f(x)g(x)
0^0 is not a limit. Neither is 1^oo, which is equal to 1. But 1^oo is often used to _represent_ a particular _form_ of limits. For example, lim(h->oo) (1+1/h)^h = e, not 1. Yet the base approaches 1 while the exponent grows without limit. Similarly, 0^0 is often used to represent the form of limits where the base and exponent both approach zero.
Various expressions fall into the 1^oo category. In general their limits don’t equal 1 or even each other. The same goes for 0^0. So what is 0^0? If you insist on 0^x being continuous, then you need limits. And in this case they do not give a unique answer. But why does it have to be continuous? If you want Sum(n=0->oo) x^n/n! to equal e^x for _all_ x, 0^0 must be 1. If you insist that 0^0 is undefined, then so is the preceding formula for x = 0. You can’t have it both ways. I choose 0^0 = 1 because I find it rather ugly to have an exception for the e^x series. In addition, every math book I have ever read which contains the series for e in summation form says that it is good for _all_ x. All x includes zero. Therefore, 0^0 = 1.
Bottom line, you have to choose between 0^0 = 1 and the summation form of the series for e^x being undefined for x = 0. Since there are many other situations where 0^0 = 1 is a very useful thing, it is wise to define it sas such.
I meant if you want y^x to be continuous at (0,0) you need limits. Sorry for the goof.
*Strictly speaking* zero to the zero power is not defined. However there are many situations where it is convenient to *assign* it a particular value. And for the vast majority of these situations, the value that works is 1.
@Richard. If you assign 1 to 0^0, you’ve defined 0^0 to be 1.
Assign and define are pretty much the same thing, but in different orders.
It is convenient to define y^0 to be 1.
It is convenient to define y^(-x) as 1/y^x for y != 0.
It is convenient to assign the nth roots of a number to the 1/nth power of a that number, using the positive root if n is even.
For real x and positive real y it is convenient to define y^x as e^(x ln y), where ln y is defined by the usual integral.
For complex numbers it is convenient to extend y^x using Euler’s formula.
For 0^0 it is convenient to assign it a value of 1.
What is the difference between these? Why are any of them “strictly speaking” more “correct” than the others?
And the clincher: According to you, Sum(n=0->oo) x^n/n! is e^x except at x = 0, where it is “strictly speaking” not defined. But it’s “convenient” to make it 1. Yet every math book I have ever seen that gives this summation formula for e^x says it is good for _all_ x. _All_ includes _0_.
Still further even also yet again: You have a choice. Accept that 0^0 = 1 (which it does), or add an exception to e^x = Sum(n=0->oo) x^n/n! for x = 0. I have yet to see any reference declare this exception, yet so many refuse to accept the inescapable consequence that 0^0 = 1.
And there’s more! It is convenient to define 0! as 1 (and, using a suitable argument [or operand], agrees with the Gamma function, which is a generalization or an extension of the factorial function).
And the same for nC0 = 1 (unless you use the factorial definition of nCk).
Why do we have all these convenient definitions and yet only 0^0 = 1 meets so much resistance from so many?
@Alan Feldman
I certainly did not mean to open a can of worms. Perhaps my choice of the words “strictly speaking” and “assign” were not the best. But I largely stand by my assertion that, applying the most rigorous standard, 0^0 is not defined. This is *not* my own proclamation, but rather what I was unequivocally taught by every math professor I had at Villanova (most of them PhD’s) in the course of obtaining my B.S. degree in mathematics (admittedly forty years ago). I agree that, when it comes to 0^0, there are times when it’s best to consider it as representing 1. But if you insist that 0^0 is formally, rigorously mathematically defined, then (unless things have changed in the last few decades) your argument is not so much with me but rather with the whole academic community.
As to why “0^0 = 1” is so controversial, I really don’t know.
Simple answer for a GCSE Student? Please no complicated things, just simple yes no, 0 or 1, thanks.
@Bobbie
I’m afraid that any simple yes no 0 or 1 answer would be inadequate. If you’re getting your information from a college math professor or a math textbook, you will most likely be told that, because of certain fundamental technical issues, 0^0 is mathematically undefined. Having said that, there are situations where 0^0 does come up, and in most of those cases it represents a 1. Some but not all math buffs take that as proof that 0^0 is fundamentally intrinsically 1; but that opinion is controversial. I realize that this is not the simple uncomplicated answer you’re looking for. But I hope you find it at least somewhat helpful.
@Richard
What is your “rigorous standard”? How is 0^0 = 1 any less valid than any of the other generalizations of y^x?
Those math professors are wrong.
Again, you cannot have e^x = Sum(n=0->oo) x^n/n! work for all numbers, but I can virtually guarantee those math professors would say the formula is good for _all_ x, and _all_ x includes _0_. So they contradict themselves. You cannot have this e^x formula work for all numbers unless 0^0 = 1. Can you please address this and my other points? You have to choose: Accept that 0^0 = 1, or add an exception to the e^x series. Please tell me what you choose.
BTW, software is drifting in the direction of 0^0 = 1. And it certainly makes programming series easier!
Please, address my points instead of quoting math professors who contradict themselves. OK.
@Bobbie
0^0 = 1
I don’t know what the test graders will assume. Just pray it doesn’t come up. I think it’s rather unlikely. But if they insist it’s undefined, they’re wrong. (^_^)
@Alan Feldman
I am not a mathematician, so I must rely on what the experts say. I’m not going to dismiss the teachings of a dozen university professors just because someone I don’t even know says they are all wrong. Please give me a few days; I will see if I can contact some of them and ask them about this. They are PhD’s who have spent their lives studying and teaching math. It’s their job to know this stuff. I trust their judgement more than I trust what I read in a discussion thread on the Internet. In the meantime, with all due respect, exactly what are *your* credentials?
Look. There are two choices:
1) 0^0 is undefined, in which case e^x = Sum(n=0->oo) x^n/n! is undefined for x = 0, and is therefore not valid for all x, or
2) 0^0 = 1, in which case e^x = Sum(n=0->oo) x^n/n! is valid for all x, including 0.
You can’t take one from column 1 and one from column 2. You must choose between 1 and 2. I keep making this point, and you keep ignoring it, as do all the other “undefiners”. Ask these professors which of the two statements is true. Let me know what they say.
This is a simple argument. If you want the series for work for x=0 you have to have 0^0=1. It cannot be otherwise, regardless of anyone’s credentials.
The mathematician here says it’s 1.
Hey, I have a reference book that says 0^a = 0 for a != 0. I don’t believe it, and never have. If a is negative, you’re dividing by 0 and that’s a big no-no.
Read my other comments in this thread. And even better, read Howard Ludwig’s.
Again, I want someone to answer my challenge of statement 1 vs 2 above. You can’t have it both ways.
Bottom line: Either 0^0 = 1, or e^x = Sum(n=0->oo) x^n/n! has an exception at zero.
You can’t have both 0^0 undefined and the series work for all x. You can’t! Ask your professors.
If you want credentials, take Euler. He said 0^0 = 1. It’s hard to outdo his credentials!
@Alan Feldman
To save space we typically write that as 
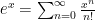with the understanding that we’re using 
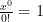, even when x=0, because the first term in the expansion is always 1. Here 0^0=1 is just a matter of notational convenience, not something particularly profound.
I hate to step into the middle of this debate. On behalf of the other readers, I genuinely appreciate that you’re having it.
The Taylor expansion of e^x is
@The Physicist
@Alan Feldman
I very much like the idea of describing 0^0=1 as “a matter of notational convenience, not something particularly profound.” I would even go one step further and call it “a matter of notational convenience, not something rigorously and fundamentally proven.” I was reading some old postings in this discussion, and I think Brian Wynne summed it up best of all in his posting of May 31, 2016, which begins: “Declaring or defining a value for a troublesome expression is not proof. How you define the value of 0^0……….” (I hope you’ll read his whole posting; I think he makes some excellent points.) My personal opinion is that there is nothing inconsistent about considering 0^0 to be undefined/indeterminate in the formal sense, and still defining it as 1 when doing so simplifies notation and/or avoids having to have special cases.
a^0 = 1, provided that “a not equal to 0”
Proof:
a ^ 0 = a ^ (1-1)
= a ^ 1 x a ^ – 1
= a / a = 1
But we know that a / a = 1 is true when “a not equal to 0” since 0 / 0 is undefined.
@Ali,
Howard Ludwig and I have explained why your argument is not definitive. In brief, you could just as well say that 0^2 is undefined, because 0^2 = 0^3 / 0^1, which is division by zero, which is undefined. Hell, you could even say 0 itself is undefined by the same argument! There are several other ways to show that 0^0 = 1. Please see posts by Howard and me.
a^k = 1·a^k
So…
a^3 = 1·a^3 = 1·a·a·a
a^2 = 1·a^2 = 1·a·a
a^1 = 1·a^1 = 1·a
a^0 = 1·a^0 = 1
Let a = 0
0^3 = 1·0^3 = 1·0·0·0
0^2 = 1·0^2 = 1·0·0
0^1 = 1·0^1 = 1·0
0^0 = 1·0^0 = 1
Maybe I’m over simplifying everything, but an exponent is an operation defined as repeated multiplication. So when 0 is the exponent, the base is never multiplied and 1 is the only factor left. This is the case for any number as well as zero.
Richard writes: “I very much like the idea of describing 0^0=1 as “a matter of notational convenience, not something particularly profound.” I would even go one step further and call it “a matter of notational convenience, not something rigorously and fundamentally proven.” ”
Not proven? Not proven based on what? How is it proven that y^x = e^(x ln y)? (Assuming positive real y and real x, of course.)
Please read my posts, and those of betaneptune and Howard Ludwig. We have addressed all these points (including Brian Wynne’s argument, which actually disproves itself!), and then some. Please tell us why our points are wrong, instead of repeating points we have addressed.
Again: We have addressed all these points. Please stop repeating them and tell us why our points are wrong.
@The Physicist
When we write the e^x formula in summation form, we are actually being more precise. There is no need to infer the pattern of succeeding terms, because it is specified explicitly.
You say then that 0^0 = 1 is simply notational convenience and not something profound. One could say the same about 0! = 1, and nC0 = 1 (the combination bit).
I suppose that by saying it’s not “profound” you mean it can’t be derived from the core definition of exponentiation, y^n = n factors of y multiplied together. So how do you derive y^(-n) = 1/y^n for n a positive integer? (And y^0, too.) You don’t and you can’t. How can you multiply something by itself a negative number of times? You can’t. So you define it to be that because it “makes sense”. It is useful and consistent with the basic laws of exponents. You do it by continuing the pattern using division. You have _generalized_ the concept of exponentiation, not derived anything. The same goes for y^x = e(x ln y). And in that case the typical derivation in calculus is to choose certain integral in a totally ad hoc manner and show it has all the right properties. You can, as Howard Ludwig has in one or more of his posts, that 0^0 has to equal 0 or 1 to satisfy the exponent laws. Choosing 0 causes an ugly exception to y^0 = 1 and is not useful for anything anyway. So it’s obviously 1.
It seems to me that by making all these definitions we are simply generalizing the idea of exponentiation in the most sensibly possible way. I mean, take 2^3.7. What does it mean to multiply 3.7 factors of 2? It makes no sense. We have done is to extend or generalize the definition of exponentiation in a useful way. One can then generalize even further to complex numbers by using Euler’s formula.
Why is 0^0 any less “profound” than the other generalizations? These other generalizations are simply ways that satisfy the exponent laws when the exponent is not a positive integer. I suppose you can say those are derivations, but it is the same as what we do to determine 0^0. And there are actually even more situations showing that 0^0 = 1. Howard Ludwig has explained this in great detail in his posts in this thread.
Please check my other posts, and those of betaneptune and Howard Ludwig, and tell us where we went astray.
@Alan Feldman
as opposed to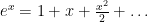 
. The second form is the Taylor polynomial and is exactly the same as e^x. The first is the same if you (fairly) define 0^0=0!=1.
My concern was that you may have been making an unwarranted appeal to authority, by claiming that e^x is defined as
I would say that 0!=1 is more convenient and that’s why we use it. And you’re right, defining y^(-n) to be the multiplicative inverse of y^n in order to be consistent with the exponential rules for positive numbers is a reasonable thing to do, but that doesn’t make it the “right” thing to do. It’s reasonable because we find that we can apply the exponential rules generally (not just to positive integers), when y^(-n) is properly defined. In fact, that is why it is so defined.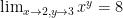
. Therefore, it is fair to define 2^3=8 (assuming that, for some reason, that was difficult to figure out directly) without any context. However, if you do the same thing for 
you find that you suddenly need to be very careful about how you do the limit. In particular, if you do the x limit first you’ll get 0 and if you do the y limit first you’ll get 1.
The particular issue with 0^0, is that there’s no one immediate “correct” definition. It’s been pointed out in this thread that you can’t “do the math” and find the value of 0^0 directly the way you can with, say, 2^3. Instead, when we bother to give it a value, it has to be in some context. For 0! there is a single defining principle (that n!=n(n-1)! and n!=1*2*3…n for n≥1) that implies that 0!=1. We need to follow a pattern and plug in a definition that works, just like with negative exponents. But that doesn’t mean that 0!=1 is “true”.
In order to define the value of something that doesn’t intrinsically have a value, we extend patterns. In this case, that generally means using limits. Regardless of how you do the limits,
This is what x^y looks like near 0^0; it’s not pretty.
That said, it is definitely reasonable, in most reasonable situations, to declare that 0^0=1.
@The Physicist
The two forms of the Taylor series for e^x are the same. Every math book I’ve ever read that gives the summation version says that it is valid for all x. “All x” includes zero. Therefore it is valid for zero. And that can only true if 0^0 = 1. Therefore, either 0^0 = 1, or all the math books are wrong and the summation version is not valid for x = 0. You can’t have it both ways.
In _Introduction to Analysis_ by Rosenlicht there is a section on power series. His proofs work only if 0^0 is defined. In one instance he talks about the series Sum(n=0->oo) c_n (x-a)^n. In some cases it converges only if x = a. So if 0^0 is undefined, such series don’t converge and the proof falls apart. Basically the radius of convergence is defined assuming the power series works at least for x-a = 0. And that can only be true if 0^0 is defined. And in the case of many series, like e^x, cos x, the binomial theorem — they only work if 0^0 = 1. So it’s 1. I’m not aware of any exceptions.
0! = 1 is true. It’s a generalization of the factorial, if you wish, as is the Gamma function! Hey, you can define n! as 1*1*2*…*n and 0! is 1 without any qualms.
You can’t “directly find the value” of the other generalizations of y^x. Why is this one any different?
Limit arguments only apply if you insist that the function be continuous. Why does it need to be continuous?
Using the exponent laws alone you can narrow down 0^0 to either 0 or 1, as Howard has shown. Series written in summation form that start with a constant require 0^0 = 1. So it’s 1.
It’s the null or empty product. It’s the number of mappings or functions from the empty set to the empty set. It works for the derivative of x^n. It works for y^0 = 1. Howard Ludwig discusses at least some of these and others in his posts. He also makes the point that why say, paraphrasing, ~”It’s undefined, but wherever it shows up you need to substitute 1. What sense does that make?~”
If 0^0 = 1 is only “definitely reasonable”, then why can’t the same be said for y^(-n), n a positive integer, y^0 = 1, and y^x = e^(x ln y)?
Please read my previous posts, and those of betaneptune and Howard Ludwig, and tell us where we went wrong.
@Alan Feldman
In the books you’re talking about, do they explicitly say “0^0=1 in all cases”, or is that only implied because it’s used? I use that convention all the time, but it’s important to be careful when you do because, to be clear, 0^0 is a known and established indeterminate form. If any book says that it has a single, definite value in all cases, then that book is definitely wrong.
No. But it has to be true for the summation formulas for power series to be valid at zero.
Indeterminate forms apply to categories of limits. Best example I can think of is 1^oo. Clearly this is one, but you can make it any positive value you want using lim(h->oo) (1+x/h)^h, which gives e^x. But clearly this doesn’t mean that 1^oo = e^x (!). 0^0 as an indeterminate form applies to an expression where both the base and the exponent go to zero as the limit is taken. It doesn’t mean that 0^0 itself is indeterminate any more than lim(h->oo) (1+x/h)^h implies that 1^oo is indeterminate. 1^oo = 1, as does 0^0.
Please read my previous posts and those of betaneptune and Howard Ludwig. We’ve already addressed all these points and much more. Please read them and tell us where we went wrong.
Why do you think that, if 0^0 is so obviously equal to 1, the entire math community has not wholeheartedly embraced it and defined it to be so? Yet, there is still something inherently unsettling about defining it for the sake of implication. Perhaps, the resistance is due to the fact that 0^0 = 1 does not hold for ALL of the different implications that arise FROM IT. You have eloquently shown a one-sided argument by clearly demonstrating so many instances that lead TO IT. But a good definition is biconditional. If your definition holds, then a^0 = 1, for ALL a, including zero. This implies that (a^0) / (0^0) = 1, for all a.
(a^0) / (0^0) ?= (a/0)^0, for all a.
@Alan Feldman
@The Physicist
@Brian Wynne
Alan Feldman writes:
“You can, as Howard Ludwig has in one or more of his posts, that 0^0 has to equal 0 or 1 to satisfy the exponent laws. Choosing 0 causes an ugly exception to y^0 = 1 and is not useful for anything anyway. So it’s obviously 1.”
This seems to suggest that difficult mathematical issues can be rigorously and formally resolved by simply rejecting what we think is “ugly” and accepting as true what we see as “useful.”
(And for that matter, what about the “ugly exception” to 0^y=0 caused by choosing 1?)
I think most would agree that pragmatically defining 0^0 to be 1 in most instances is useful and logical. But that’s not the same thing as establishing by rigorous proof that 0^0 is fundamentally, intrinsically, and exclusively equal to 1. The sigma notation for the Taylor series for e^x (and for any Taylor series for that matter) does not prove that 0^0=1. The reason for assigning the value 1 to 0^0 in the first place is to make it “work” for that (and similar) notation. Using that notation as proof is begging the question.
It’s time to close this discussion.
Those high-school math teachers] (if they insist that 0^0 is 0 or undefined) are just plain wrong. They do correctly assert that x^0 = 1 for x > 0, so they will concede that e^0 = 1 (where e=2.71828… is the base of natural logarithms).
The definition of the fundamental exponential function exp(x) = e^x , is:
exp(x) ≡ Σ(k=0, 1, … ∞) x^k/k!
In the simplest case, exp(0) = e^0 = 1 , all but the first term in the series vanish because for k>0, 0^k = 0 and k! > 0 (so 0^k/k! = 0). This leaves
exp(0) = 1 = 0^0 / 0!
and since 0! = 1 (a settled fact),
0^0 = 1
QED.
It is time to close this discussion.
@Brian Wynne
You ask
(a^0) / (0^0) ?= (a/0)^0, for all a.
No. This doesn’t work for any a. And the reason it doesn’t work is that the exponent laws are not valid when there is division by zero. But it is still true that 0^0 = 1.
The fact that you can’t express the LHS in the form of the RHS means nothing as to the value of the LHS.
Nonsense from nothing:
0 = 0
a^2-a^2 = a^2-a^2
a^2-a^2 = a(a-a)
a^2-a^2 = (a+a) (a-a)
(a+a)(a-a) = a(a-a)
a+a = a
2 = 1
The above also doesn’t work when you allow division by zero, which is what you’re doing when you cancel the (a-a)’s. This doesn’t mean that and of the equalities before canceling out the (a-a)’s aren’t true.
@Richard
I’m still waiting for the “rigorous proof” that y^x = e^(x ln y). And when you prove it you have to state your assumptions. The only “pure” case is the basic exponent laws with positive integral exponents. The rest is generalizing via definitions.
And you clearly didn’t understand my points. Let’s try again:
There are times when multiple solutions come up. You are allowed to reject the nonsensical ones. What is the length of a side of a square with an area of 4? Well, we know that the area is the length squared, so we can say that L^2=4. This gives L=+/-2. We reject the -2, as it is meaningless, and have rigorously proven that the side of the square is 2. We do similar things in physics. The integral of the wave function over all space is not allowed to become infinite. So any wave function that grows without limit as x increases is properly rejected, even though it may be a solution of the Schroedinger equation. So by using the basic exponent laws we can easily show that 0^0 has to be zero or 1. Everything else points to 1. So it’s 1. We reject the bad answer just as we do in many other cases. Remember, the exponent laws are not enough to determine an an answer, but it offers a solution that is consistent with every other method of determining 0^0. You are focusing on the exponent-law argument to the exclusion of everything else. You are “cherry picking”, or whatever its opposite is. Everything I have said in totality clearly points to 0^0 = 1.
As for my summation format argument, again you missed the point. Every book that gives the formula for e^x in summation form also says it is valid for all x. All x includes 0. There are no asterisks with side conditions or what not. All x means all x. And for the formula to be true for 0, 0^0 has to be 1. As I’ve said many, many times, you have two choices:
1) 0^0 = 1 and e^x = Sum(0->oo) x^n/n!
-XOR-
2) 0^0 is undefined, and therefore we have an exception in the e^x formula for x = 0, meaning that the formula is not true for all x.
Please choose 1 or 2. Don’t sidetrack into other arguments as you’ve just done. Don’t tell me it doesn’t prove anything. Don’t go off on any other tangents. This is a simple question: Is it 1, or is it 2? You can’t have it both ways.
No one has answered this question. You can be the first.
Wow, I spoke too soon! STEPHAN H. has answered my question. And the answer is 1. Thank you STEPHAN H.
OK.
@STEPHAN H.
If you feel the discussion should close, then I don’t think it’s such a good idea to make a posting declaring that you are right and proclaiming to all who disagree with you that we are wrong. That’s like sending us engraved invitations to continue presenting *our* arguments.
I actually agree with you that it’s getting to be time to end the discussion, for the simple reason that it’s just not getting anywhere. No one is changing anyone’s mind about anything.
I feel a good way to move in that direction is to see if there is something, no matter how small or trivial, that we can all agree on. Something like:
One of the most debated controversies in mathematics is the question of zero to the zero power. This issue has been argued for centuries, and the disagreement is not likely to end.
I doubt anyone would disagree with that. And I suspect it’s probably the only thing we’ll all be able to agree on.
@Richard, who writes:
“Alan Feldman writes:
“You can, as Howard Ludwig has in one or more of his posts, that 0^0 has to equal 0 or 1 to satisfy the exponent laws. Choosing 0 causes an ugly exception to y^0 = 1 and is not useful for anything anyway. So it’s obviously 1.”
This seems to suggest that difficult mathematical issues can be rigorously and formally resolved by simply rejecting what we think is “ugly” and accepting as true what we see as “useful.”
(And for that matter, what about the “ugly exception” to 0^y=0 caused by choosing 1?)”
Sorry, but I have more to add.
There’s another ugly thing and it occurs with y^x = e^(x ln y).
We have the exponent law y^m y^n = y^(m+n). Clearly this works for positive integral exponents. But when we try to extend to rational exponents, we run into a problem.
What should 4^(1/2) be? Well, we want it to satisfy the exponent laws. And with this one we have
(+/-2)^2 = 4. But we want a unique value. So we throw out the negative one. We need to do this for all even roots. But the above formula does it for us. So even with this accepted formula we are throwing out ugly values, in no small part because it’s useful to do so.
Now I completely forgot to comment on 0^y = 0. I don’t think it’s ugly to choose 0^0 = 1. Zero is a special case. E.g., you can’t take 0 to a negative exponent (and probably not an imaginary one, either). Notice that we set 0^y for positive real y to be 0. For positive integral exponents this is obvious. But we do it for the in-between values because it makes the exponent laws work. And notice that we can’t use the log definition! Additionally y^0 is far more important than 0^y. Maybe instead of ugly I should have said impractical. But remember it’s much more than this that shows that 0^0 = 1. Much more. Howard Ludwig, betaneptune, and I have written much about that in our other posts.
OK.
(Second attempt to post this; the captcha keeps messing things up.)
@Alan Feldman
You wrote:
********************
“As I’ve said many, many times, you have two choices:
1) 0^0 = 1 and e^x = Sum(0->oo) x^n/n!
-XOR-
2) 0^0 is undefined, and therefore we have an exception in the e^x formula for x = 0, meaning that the formula is not true for all x.
Please choose 1 or 2. Don’t sidetrack into other arguments as you’ve just done. Don’t tell me it doesn’t prove anything. Don’t go off on any other tangents. This is a simple question: Is it 1, or is it 2? You can’t have it both ways.”
********************
I would still say both.
If you replace #2 with:
“2) 0^0 is an indeterminate form.”
then I don’t think that creates a prohibitive contradiction. An indeterminate form can be interpreted/defined in different ways in different circumstances. In any case I don’t think it would be any more contradictory than a physicist defining light as simultaneously a wave and a particle even though waves and particles are not at all the same thing. This allows a physicist to use whichever definition works in any particular situation. My personal opinion is that this is the optimum (though not necessarily perfect) answer to the 0^0 question.
============
@Alan Feldman
@STEPHAN H.
@The Physicist
@Brian Wynne
While I disagree with STEPHAN H’s opinion on defining 0^0, I wholeheartedly agree with him that it’s getting to be time to wrap up this discussion. It’s leading nowhere. No one is changing anyone’s mind about anything. Why don’t we all just agree that zero to the zero power is a controversial issue and let it go at that.
@Richard:
Two reasons:
1) I can’t let the indeterminate thing go unchallenged.
As Howard Ludwig, betaneptune, and I have said again and again, indeterminate forms apply to limits, not values. They give a way to _classify_ various types of limits.
1^oo = 1
lim(h->o) (1+xh)^(1/h) = e^x
This is a limit of the type 1^oo. Saying 0^0 being an indeterminate form means it’s undefined is like saying 1^oo = e^x because of the above equation.
2) Physics.
OK. I can’t let you get away with that. Numbers are not particles. They are not waves. They are not probability densities. They are numbers. They have unique values. There’s no point in having numbers that aren’t.
Particles exhibit wavelike character and a particle-like character. The two characters are complementary. Like a woman can be a daughter, wife, grandmother, insurance saleswoman, astronaut, etc. Quantum mechanics includes acausal behavior, which is pretty much the antithesis of the behavior of numbers.
“This allows a physicist to use whichever definition works in any particular situation.” They are not definitions. They are characteristics. Experiment (when properly done!) says what’s right.
@Alan Feldman
. It follows that, unlike in the case of 0!, 0^0 does not have a value associated with it that can be used generally.
The indeterminate form keeps coming up because, lacking an intrinsic, derivable value, another value must be assigned. What value to use is generally determined by looking at the behavior of the function nearby. 0^0 is indeterminate because x^y doesn’t approach a particular value as
(I don’t know when or even if this posting is going to go through. I’ve been having huge difficulties in the last few days with the captcha (which never even used to show up).)
@Alan Feldman
I think it’s clear that there is never going to be total agreement on this. I wish we could just agree to disagree.
@RICHARD:
i’m sorry, but by saying “both” you disqualify yourself from logical discussion, because option one is a conjunction which includes the statement that zero to the zero power is defined as one, in direct contradiction to option two’s statement that zero to the zero power is not defined (even though by choosing this option you would make “the most important function in mathematics”, the exponential function, either undefined or unnecessarily complicated at the simplest element of its domain, zero).
Let us agree, for the sake of convenience and epistemological honesty, that it is axiomatic (a useful definition and not a theorem) that
0º ≡ 1
And let’s be clear: Option one actually requires us to say that while the object in question is undefined, the exponential function is unnecessarily complicated at _every_ point in its domain. Our choices are EITHER
0^0 is undefined AND
exp(x) ≡ 1 + ∑ (k=1 … ∞) x^k / k!
OR
0^0 ≡ 1 AND
exp(x) ≡ ∑ (k=0 … ∞) x^k / k!
Oh, and the quibblers also have to explicate special cases for the binomial theorem and other beautiful truths which have been published in their simple and elegant form for centuries.