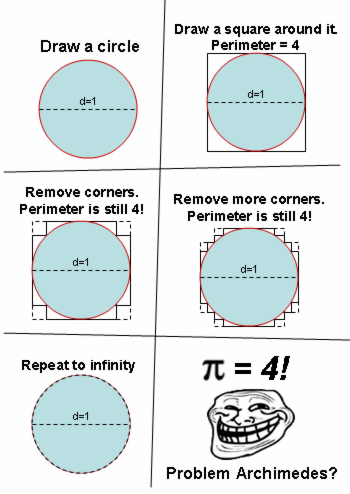
Physicist: Recently this picture has been floating around confusing everyone, and making people think that maybe Indiana wasn’t completely off base when they moved to declare that .
The exact answer to this question comes from deep in the field of mathematical analysis, which is where mathematicians go to think up worse-case scenarios. That answer is long and uninteresting. This answer is better.
This zig-zag path does approach the circle, so on the surface of it you’d expect that it would have the same length. However, the length of a curve is more a function of it’s derivative (slope), and less a function of its position. If you were to throw a jumbled up 20 foot rope into a 1 foot box, you wouldn’t say that the box is 20 feet across. You’d want to straighten the rope out before you draw any conclusions.
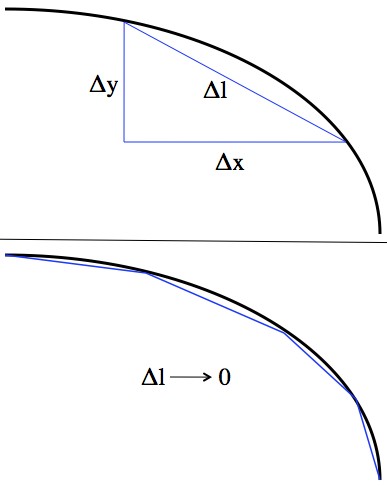
To find the length of a curve you approximate it with lots of straight lines, then let the number of those lines go to infinity, and the lengths of the individual lines go to zero.
Using the Pythagorean theorem: . So if the total length of the curve is L, then by adding up all the little pieces you can get a good approximation:
When the lengths get very small (that is, when ),
becomes
,
becomes
, and
becomes
. This is just a Riemann sum.
Now you have (one version of) the arclength equation: ! Notice that the approximation has now become an equality.
If you were/are a calculus student, that “dy/dx” probably just set off some alarms in your head. dy/dx is the “derivative of y with respect to x”. If you were to make a graph of y vs. x, it would be the slope of the graph, and (this is the important part) L depends on it explicitly.
So finally, to answer the question, in order to approximate a path with another path, in such a way that they end up having the same length, you must be careful to make sure that the two paths have the same slope along their entire length.
As an aside: The “problem Archimedes?” thing is a reference to Archimedes’ approximation of
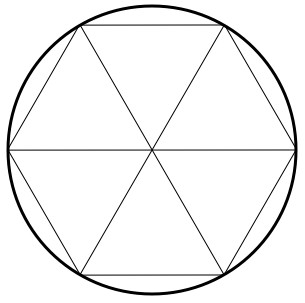
In this case, since the higher the number of sides the n-gon has, the better it approximates the circle both in position and slope, you’ll find that as ,
! The
inside the Sine function falls out of the definition of “radians“, and basically boils down to the usual definition.







I was gonna write to you a few months ago about a similar
“proof” that the diagonal of a unit square is equal to 2, but while
I was composing the email I realized pretty much what you wrote
here.
Hahah someone should make a version of that picture for a right triangle, and declare that the hypotenuse = sum of two sides.
This is sort of a follow up question: Matter isn’t infinitely dividable, so even if you move diagonally your still crossing the same amount of atoms. How come it is still faster? I hope this made sense…
John, geometry may have wonderful applications in the real world where atoms and the Heisenberg uncertainty principle reign supreme but there is nothing to stop one mathematically defining a line with features infinitely more minute than an atom. In fact because a line is a 1-d object you can make it zig-zag so much that you end up with a shape that has a finite area but an infinite circumference and nobody bats an eyelid.
my quetion to google was/is, what is meant by the seven lengthed circle of pythagoras? I do not expect to have answers in terms of atoms and photons of energy. Answer please.
There’s some debate about whether that refers to seven wise men, the lengths of seven different circles, seven photons of energy, or the (provably impossible) inscribing of an exact heptagon into a circle.
Pythagoras was into all kinds of freaky stuff (numerology), so a fair fraction of the Pythagoras stuff you may come across is going to be pretty useless.
Rather than think about a circle, we could just think about a square with a diagonal line from one corner to the other…Naturally the shortest distance from one corner to the other is that diagonal straight line, but it isn’t the only way we can get there.
If we drove one mile north and then one mile west, our total driving distance would be 2 miles. However if we drove NW directly(turned the car 45 degrees and drove the straight route), the total distance would be the square root of two miles. We could subdivide out north, then west route as well…i.e., drive 1/2 mile north, 1/2 mile west, another 1/2 mile north, and another 1/2 west to reach the destination, but it isn’t any shorter than the original 2 mile trip. In fact, every time you subdivide your north then west path, it still always adds up to 2 miles because the north components always add up to 1 and the west components always add up to 1 as well.
Just because you can’t “see” the jagged pattern, doesn’t mean that the jagged pattern has become a diagonal line. Really, it is a matter of “zooming in” to see that the jagged pattern remains.
sir i am reading in 12th and i can notknow how it is possible.
Couldn’t one solve it using something similar to an SDE integral? Knowing that the infinitesimal generated has non-zero variation, an additional term pops out based on that. So 4 = pi + non-Riemann variation term. The geometric argument you make above, leads directly to finding what the term is.
All of this can be summarized by: limit (length of curves of a sequence of curves) is equal to lengt(of acurve which is the limit of a sequence of curves) only under specific conditions.
The problem with geometrical approach is that you ‘forget’ the transition from ‘countable infinity’ towards ‘uncountable infinity’.
If you divide any line which goes around the circle in two you will never ever approach this circle. This is because you ‘miss’ much more places at which you can hit the circle with these sides of the triangles. This is similar to the following:
pick the interval [0, 1]. pick the midpoint og this interval (1/2). you now have two intervals. Pick midpoints of both intervals (1/4, 3/4). You now have the following midpoints (1/4, 1/2, 3/4). Do the same with the newly created intervals, i.e. you now have (1/8, 2/8, 3/8, …, 7/8). Apply the above procedure ‘infinite’ times.
Do you think you hit *all* number within the original interval [0,1]? Answer: no.
What you wrote down is a list which is ‘countable infinite’ long. However, one can prove (Cantor’s diagonal argument) that there are much more numbers you did not write down. Therefore you will never be able to write down all the numbers.
Apply this thought to the original question of pi and you will see that you will never hit *all* points on the circle and therefore you will never approach this circle.
There is a very simple way to prove whether pi is 4 or not. It is not a very technical experiment, although it is scientific (since science requires observation, and it is readily observable.)
Measure the diameter of a cup you have around the house. Let’s say the diameter is 2.5 inches. Since the circumference of a circle is pi times diameter, just multiply 2.5 by whatever you believe pi to be. If you believe pi to be 4, then multiply 2.5 times 4. So that gives you 10 inches. Now cut a piece of paper or string or whatever to 10 inches. Tape one edge of it to the side of the cup and wrap it around the cup. If pi is 4, then the ends of the paper or string will meet. If it isn’t, then it won’t.
This is an elementary school type experiment that pretty much anyone could do.
Using Dan’s simple experiment seems to have hit the nail on the head. A cup with a 3inch diameter has a circumference well short of 12 inches. Ergo Pi<4.
I believe it has to do with the “Phi ratio”. Perfect geometrical patterns in every organic being. Wether human, plant, animal, celestial, galactic, universal…
It all has the “Phi ratio” in it.
Not the Pi = 4 or the controversy all together.. but more the phoanetic “Fy” or the 21st letter of the greek alphabet.
The Odd Ones Out gave a much simpler explanation. Also, aren’t all “perfect” circles using 4 as pi, given that pixels are square? zoom up really close, and it will look exactly like it does if the pi=4 paradox, with the corners infinitely removed.
Here is a funny thing….try the trick of proving pi=4….but…measure the area inside the scrunched up square….you will be amazed (i was 😊)..area is equal to circle area….so the same approximation which gives WRONG PERIMETER gives RIGHT AREA….this has to do with the idea of “order of error”…
π is just 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986 and it speak out like tran·scen·den·tal but what is it?
here is the the 1st 10st of π
3.1415926535
but what about the double of π you don’t speak out like 6.28318530718… no there a easy to speak out like π then is t then come p this all are GReeCE letters
But when you search up of a image of circle and Zoom in, they are made of square pixels so Pi=4
🤔🤔😂
Y’all are nerds
Cool