Physicist: This probably should have come before the last post.
Length contraction is a symptom of “tilted now planes”. For someone moving past you events physically in front of them happen earlier than they should (according to you), and events physically behind them happen later (according to you).
Here’s the idea in a nutshell: you’re in the middle of a train when the front and back are hit by lightning. People on the train will see the lightning at the front of the train a little earlier than someone on the tracks because they’re moving toward it, and will see the lightning at the back of the train a little later because they’re moving away from it. At least, that’s the way someone on the tracks would explain it.
However, the laws of physics are blind to “uniform movement”. That is, all physical laws are exactly the same whether you’re moving (at a constant speed) or not. And that’s relativity. So both points of view are equally correct. That summary was a little fast because it’s covered in a lot more detail here: Q: According to relativity, two moving observers always see the other moving through time slower. Isn’t that a contradiction? Doesn’t one have to be faster?
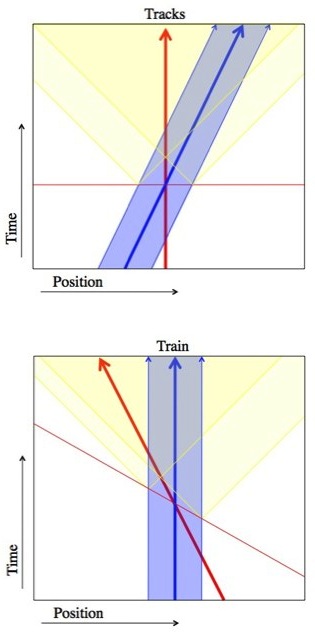
Someone of the tracks (blue) sees lightning hit the front and back of a train, simultaneously, as it passes by. Someone on the train (red) sees the lightning at the front first. Both are right. So, in general (not just with lightning), when someone passes by events happening physically in front of them happen a little sooner than they should (according to you).
The traditional example is the barn-running pole-vaulter thought experiment.
A pole vaulter runs through a barn very, very fast with a pole that (when it’s standing still) is about as long as the barn. From her point of view the barn, which is rushing past her, is contracted so that her pole (briefly) is sticking out of both ends of the barn. The farmer, who leaves the doors to his barn open, because this happens all the time, sees the vaulter and her pole contracted so that (briefly) the entire pole is inside the barn.
They’re both right, and here’s why! Consider the two events (A) the back of the pole entering the barn and (B) the front of the pole exiting the barn.
For the farmer event A happens first, then event B happens second.
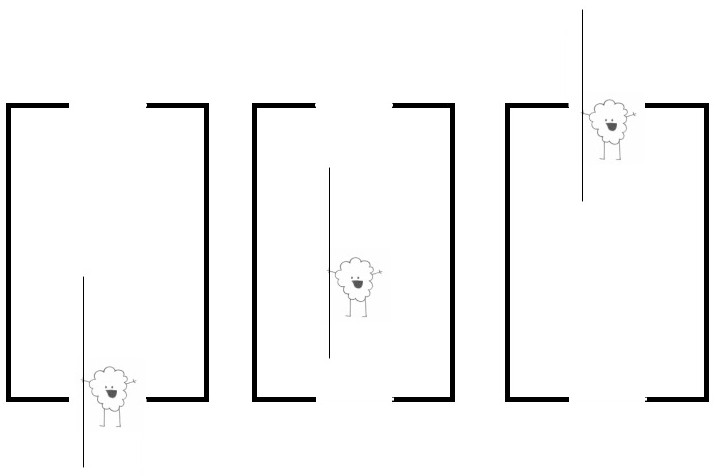
For the farmer the back of the pole enters the barn before the front of the pole exits the barn. Obviously, the pole shrank.
The pole vaulter sees the same process, but sees the events in front of her happening sooner, and the events behind her happening later. So, in this case, she sees event B first and event A second.
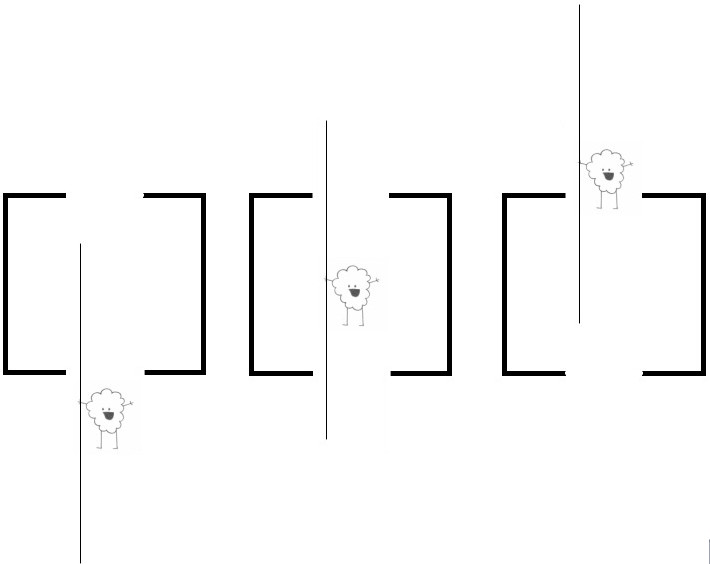
For the pole vaulter the front of the pole exits the barn first, and then the back of the pole enters the barn. Obviously, the barn shrank.
So, time dilation, length contraction, and the rearrangement of events are just three sides of the same weirdly shaped coin.
I should point out, that there’s a weakness in the language that makes it sound like relativistic effects aren’t real events; “from one point of view…”, “when one person looks at the other they see…”, etc. Length contraction is a completely real effect. At very high speeds objects really do contract in the direction of motion. However, you have to be really trucking along before it becomes an issue. What follows is answer gravy.
Answer gravy: The best way to describe how strong relativistic effects are is to use “
That whole opening it to explain why relativistic effects are so unnoticable. Below is a graph of speed on the x-axis (from 0 to c) and gamma on the y-axis. Just to put things in perspective I’ve included some sample speeds, that people have experienced.
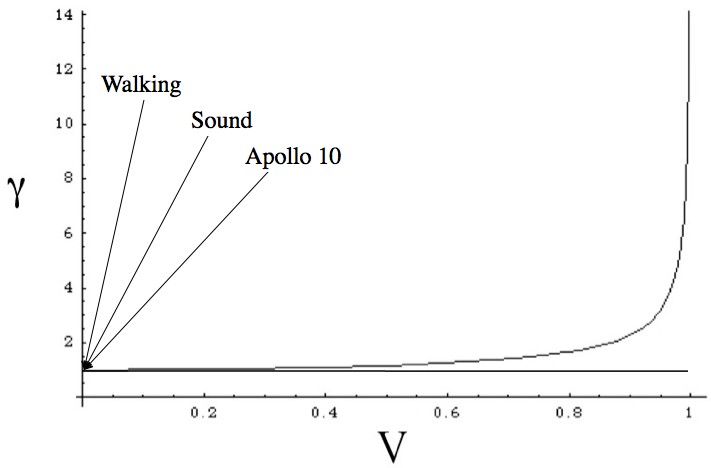
No one has ever experienced a relativistic effect that they could feel. We can measure the effects, but the effects are extremely small on the everyday scale. The horizontal line is "gamma = 1".
The Apollo 10 service and crew modules (the fastest manned vehicle ever) managed to get all the way up to 0.0037% of light speed, which is just unimaginably fast. Commander Stafford, et al., experienced a 
More gravy!: Mathematically, the way a physicist might describe length contraction (more exactly) would be to use the “spacetime interval“. If you have two events happening at the points 
S is useful because, although relativistic effects change the x’s and t’s and whatnot, S remains constant for everybody. Here goes!
When something is sitting still the way you measure it is to get out a ruler. When something is moving past you the way to measure it’s length is to time how long it takes to get past a point. If it’s moving at 10 kph and it takes 2 hours to pass, then it must be 20 km long. So, we have two events. When the front of the object passes the measuring point, and when the back of the object passes the measuring point.
The length of an object in the frame where something is sitting still, we’ll call “L”. When something is moving it’s length is LM.
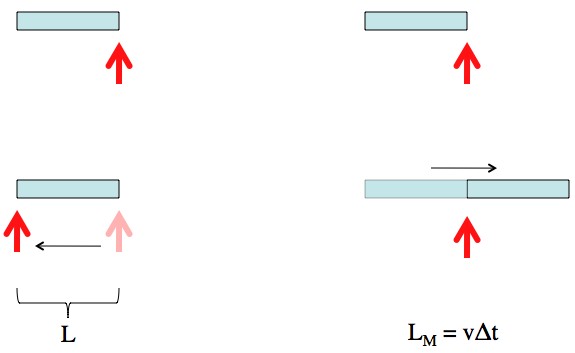
An object moving past an arbitrary point used for measurement. In the objects stationary frame the arrow is doing the moving, and in the arrows frame the object is doing the moving.
In the stationary frame:
Similarly, in the moving frame:
But, the spacetime interval is always the same, even if everything else is different. So:
Gamma again! Good times!
Pingback: Q: Why does E=MC2 ? | Ask a Mathematician / Ask a Physicist
Pingback: Q: Why does going fast increase an object’s mass? | Ask a Mathematician / Ask a Physicist
Pingback: Q: How do velocities add? If I’m riding a beam of light and I throw a ball, why doesn’t the ball go faster than light? | Ask a Mathematician / Ask a Physicist
Pingback: Q: Do time and distance exist in a completely empty universe? | Ask a Mathematician / Ask a Physicist
is length contraction is real, and not only relativistic, does that mean that i am right now really contracting, and dilating, relative to many particles, starts etc moving at near c speeds from me?
Yup!
Pingback: Q: If a photon doesn’t experience time, then how can it travel? | Ask a Mathematician / Ask a Physicist
If you”re traveling just under the speed of light away from earth and send a radio message back, what would happen ?
It would be red shifted.
Pingback: Q: According to relativity, things get more massive the faster they move. If something were moving fast enough, would it become a black hole? | Ask a Mathematician / Ask a Physicist
Perfectly correct as I see it, the complementary principle to that Moya is that depending on frame of reference chosen, measuring yours, your ‘time’ also will be found to eh, ‘flounder’? That doesn’t speak about your local ‘proper time’, but about relationships between uniformly, or accelerated, frames of reference. It’s a pretty weird universe, although locally ‘invariant’.
still don’t understand *why* it happens. what’s the mechanism? everyone’s always mentioning what observers “see”, making me think it all has to do with light. if i try the reductionist approach i always get to light hitting observers sooner or later, which makes it seem an artifact more than a real phenomenon. if it’s the latter, i’ve yet to come across a meaningful explanation. looks like the only way might be to get into the math until i’m good enough, and then wade through einstein’s own notes and papers.
Spaceman heading to star 10 light years away, as measured by Ground Control on Earth.
Speed attained is close to the that of light.
Does the actual distance contract that the spaceman has to travel?
@Paul Quinn
From the spaceman’s point of view: yes, the distance to the distant star literally becomes shorter.
Thanks for that really appreciated.
So, does the period taken for the Spaceman to reach the 10 light year away star (distance divided by speed), now take less time, than had been calculated prior to the journey (due to the shorter distance now being experienced as a consequence of length contraction) or does time dilation result in the actual journey time equalling the calculation prior to setting off?
@Paul Quinn
Length contraction and time dilation are two sides of the same coin. Everybody can agree that when the space man gets where he’s going his watch will read less that it “should” have. Ground control would say that the distance was the same but the space man’s clock was running slow (time dilation). The space man would say that the distance was shorter and that his watch ran normally (length contraction).
Superb. Thanks.
the Lorentz contraction is a illusion produced by the not symultaneouly of the events due the constancy of light speed that generate in differents observers with speed near the speed of light
I looked at this and many other examples online and still not buying it.
I can understand that we observe things and things will look different to different people based on movement and their location. And I love the maths to work out what length an object will appear as.
But just because of the order of events may be screw-if and B fore A, to me does not change the facts that the pole is still shorter than the barn.
In fact I noticed you talk about the pole being longer then in your next paragraph (after you say its real) we jump into being shorter with length contraction. SO to me you used an example to prove the opposite . bit lost me there.
And why is it real. If I pressed Pause on the universe at that exact moment as the pole vaulter and the rod stayed in place and I walked around it. I do not believe it would be longer than the barn. But was only being observed longer than the barn.
I had this story. If a space ship at light speed travelled 25 light years to earth. It wold take 25 years for the light of that event to arrive and at the ship being 24 lights years out, would take 24 light years to arrive and so on. So when it gets to earth, assuming you could see it all. The light from all events would arrive all at once.
So the Ship would appear to be 25 light years long for a moment in time.
Well truth is the ship is still the same length, but all we are seeing is the effect of light bringing the image to us out of event.
Maths can be used to work out length dilation based on an observation, but I think it is being used the wrong way around. Objects look longer at speed, and we use their speed and reverse engineer the length to work out the actual length of the object.
But I could be wrong and everyone contradicts the way I see it, but I am yet to be convinced. Can you help
@Mark Whorlow
You put your finger on it when you described “putting the universe on pause”. The problem is that there’s no “universal clock”. Different perspectives disagree not only on how fast time is passing, but also on what “now” means. From the point of view of the pole vaulter’s perspective “now” is a time after the front of the pole has left the barn and before a time when the back of the pole has entered, and from the farmer’s perspective “now” includes a time before the front of the pole has left the barn and after the back has entered.
The effect you described at the end, with a ship approaching at the speed of light, is a strictly visual effect. It’s a little like distant objects appearing to be smaller; they look smaller, but it’s not difficult to figure out how big they really are. Similarly, the ship looks stretched out, but it’s not difficult (if you’re familiar with relativity at least) to figure out how big it really is.
Pingback: Q: In relativity, length contracts at high speeds. But what’s contracting? Is it distance or space or is there even a difference? | Ask a Mathematician / Ask a Physicist
In the pole vaulter example, I can see why the pole vaulter views the pole as longer than the barn because they are approaching the front of the pole and moving away from the back of the pole. However, I don’t understand why the farmer would see the back of the pole enter before the front of the pole exits. In the train track example the observer who was stationary relative to the lightning strikes saw them happen at the exact same time not one before the other. in the pole vaulter example the farmer is also stationary relative to the two doors of the barn. so how come the farmer doesn’t see the pole enter the back and leave the front of the barn at the exact same time, the same way that the person standing on the tracks viewed the lightning strikes at the same time?
@Conor
The briefly shut barn doors take the place of the lightning strikes, not the ends of the pole passing through the doors. The farmer sees them simultaneously closed for a moment, with the pole vaulter inside. The pole vaulter sees the door in front of him briefly closed first, then a little later the door behind him closed.