Physicist: When you have two finite sets it’s easy to say which one has more things in it. You count up the number of things in each, compare the numbers, and which ever is more… is more. However, with an infinite set you can’t do that. Firstly, you’ll never be done counting, and secondly, infinity isn’t a number.
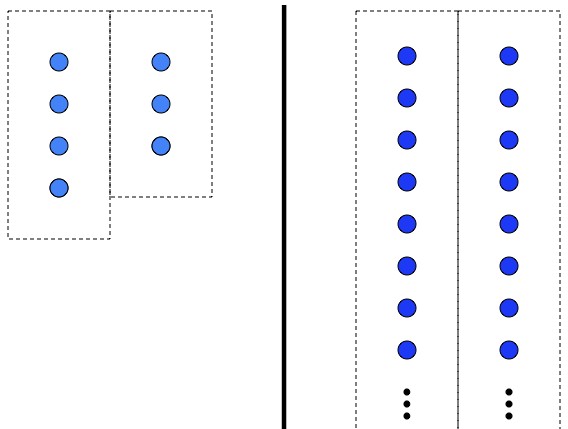
With finite sets you just compare the number of elements in each set (left), but with infinite sets that’s not an option (right). Phrases like “number of elements in the set” don’t apply.
So now you need to come up with a more rigorous definition of “same size”, that reduces to “same number of elements” in the finite case, but continues to work in the infinite case.
Here it is: instead of counting up the number of elements, and facing the possibility that you’d never finish, take the elements from each set one at a time and pair them up. If you can pair up every element from one set with with every element from another set, without doubling up and without leaving anything out, then the sets must be the same size.
Mathematicians, who enjoy sounding smart as much or more than they enjoy being smart, would call this “establishing a bijective mapping between sets”.
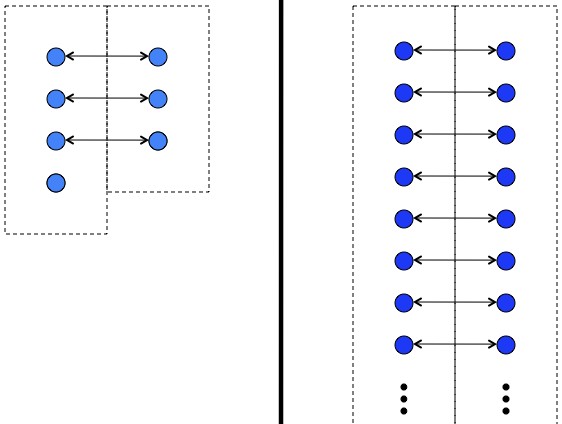
By pairing up elements you can establish that the sets have the same number of elements. The sets on the left have an unequal number of elements, and the sets on the right (somewhat surprisingly) have the same “number” of elements.
So the requirement for two sets to have the same size is that some pairing exists. For example, in the right side of the picture above you could have chosen to pair up every element in the left column with the element below and to the right forever, leaving the one element
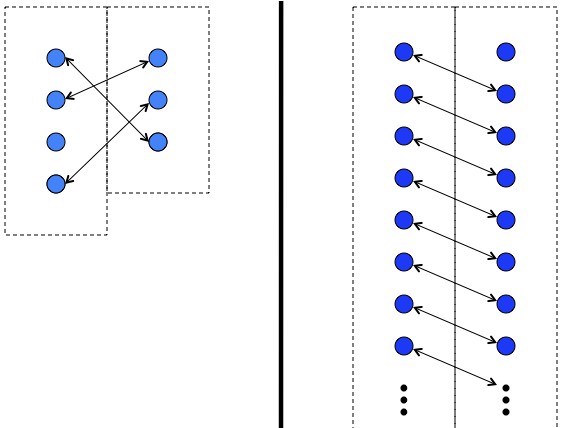
If you rearrange the pairing for finite sets you’ll find it has no effect: there will be the same number of unpaired elements. Infinite sets are not so restricted. Literally, ∞ +1 = ∞.
Even worse, you can show that two sets that have “obviously” different sizes are in reality the same size. For example, the counting numbers (1, 2, 3, …) and the integers (…, -2 , -1, 0, 1, 2, 3, …):
One of the classic “thought experiments” of logic is similar to this: You’re the proprietor of a completely booked up hotel with infinite rooms. Suddenly an infinite tour bus with infinite tourists rolls up. What do you do? What… do you do?
Easy! Ask everyone in your hotel to double their room number, and move to that room (where there should be a gratis cheese basket with a note that says “sorry you had to move what was most likely an infinite distance“). So now you’ve gone from having all of the rooms full to having only all of the even rooms full, while all of the odd rooms are vacant.
Another way to look at this is: ∞ + ∞ = ∞.
Here’s something even worse. There are an infinite number of primes, and you can pair them up with the counting numbers:
There are also an infinite number of rational numbers, and you can pair them up with the counting numbers.

Arrange the rational numbers in a grid, then count diagonally in a loop. This is the traditional way to “ennumerate” the rational numbers.
By the way, you can include the negative rationals by doing the same kind of trick that was done to pair up the counting numbers and integers.
Now you can construct a pairing between the rational numbers and the primes:
For those of you considering a career in mathing, be warned. From time to time you may be called upon to say something as bat-shit crazy as “there are exactly as many prime numbers as rational numbers”.
There are infinities objectively bigger than the infinities so far. All of the infinities so far have been “countably infinite”, because they’re the same “size” as the counting numbers. Larger infinities can’t be paired, term by term, with smaller infinities.
Set theorists would call countable infinity “” (read “aleph null”). Strange as it sounds, it’s the smallest type of infinity.
The size of the set of real numbers is an example of a larger infinity. While rational numbers can be found everywhere on the number line, they leave a lot of gaps. If you went stab-crazy on a piece of paper with an infinitely thin pin, you’d make a lot of holes, but you’d never destroy the paper. Similarly, the rational numbers are pin pricks on the number line. Using a countable infinity you can’t construct any kind of “continuous” set (like the real numbers). You need a bigger infinity.
The number line itself, the real numbers, is a larger kind of infinity. There’s no way to pair the real numbers up with the counting numbers (it’s difficult to show this). The kind of infinity that’s the size of the set of real numbers is called ““.
Before you ask: yes, there’s an ,
, and so forth, but these are more difficult to picture. To get from one to the next all you have to do is take the “power set” of a set that’s as big as the previous
. Isn’t that weird?
A commenter kindly pointed out that this “power set thing” is a property of “ numbers” (“beth numbers”). But, if you buy the “generalized continuum hypothesis” you find that
. This is a bit more technical than this post needs, but it’s worth mentioning.
Quick aside: If A is a set, then the power set of A (written 2A, for silly reasons) is the “set of all subsets of A”. So if A = (1,2,3), then 2A = (Ø, (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3) ). Finite power sets aren’t too interesting, but they make good examples.
Update: The Mathematician was kind enough to explain why the real numbers are the size of the power set of the counting numbers, in the next section.
Strangely enough, there doesn’t seem to be infinities in between these sizes. That is, there doesn’t seem to be an “” (e.g., something bigger than
and smaller than
). This is called the “continuum hypothesis“, and (as of this post) it’s one of the great unsolved mysteries in mathematics. In fact it has been proven that, using the presently accepted axioms of mathematics, the continuum hypothesis can’t be proven and it can’t be dis-proven. This may be one of the “incomplete bits” of logic that Godel showed must exist. Heavy stuff.
Mathematician: This isn’t rigorous, but gives the intuition perhaps.
Let’s suppose we think of each natural number as representing one binary digit of a number between 0 and 1 (so the nth natural number corresponds to the nth binary digit). Now, the power set is the set of all subsets of the natural numbers, so let’s consider one such subset of the natural numbers. We can think of representing that subset as a binary number, with a 1 for each number in the subset, and a 0 for each number not in the subset. Hence, each element of the power set corresponds to an infinite sequence of binary digits, which can just be thought of as a number between 0 and 1. Then you just need a function from [0,1] to all of the real numbers, like , which leads us to believe that there should be a function mapping each real number into an element of the power set of the natural numbers.








GCH isn’t exactly the type of “incompleteness bits” Godel showed must exist. I mean, of course it is an example of incompleteness, but it’s more sophisticated than the Godel incompleteness theorems. It uses forcing. Whereas Godel’s theorems dealt with silly self-referential paradoxy sentences like “This sentence is false”, in order to prove the independence of GCH, you must construct a model of ZFC where GCH is true (so ZFC can’t disprove GCH) and then construct a model of ZFC where GCH is false (so ZFC can’t prove GCH).
Could you explain why the cardinality of R should be the cardinality of the power set of N? I can’t imagine why that should be so.
How does one apply that to infinite points in space?
Or to rephrase, there are an equal amount of points in a marble as there are in the sun, correct?
If the center a sphere can be defined as the origin (0,0,0), there are infinite degrees upon which one can cut a cross-sectional 2D plane intersecting the origin, and upon each of those 2D planes one can plot infinite points, thus both the marble and the sun, while having vastly different volumes, have infinite points
I know I answered it myself, but can you do an extended explanation similar to the original post?
Also, which power set does this infinite fall into?
The bijective map between the marble and the sun is just a scaling. So, line up the centers, then multiply the distant of each point in the marble by some huge number, so that it lines up with the sun’s size.
All finite dimensional (Euclidean) spaces fall into the aleph 1 category.
To see that, what you can do is take a point in, say, 2-D space: (1.234567…, 9.876543…). Then define a bijection from 2-D real space, to 1-D real space (the real line) by “inter-weaving” the digits: 19.283746556473…
You can extend the same idea to higher dimensions no problem. So, any number gives you a unique point in 3-D space, and any point in 3-D space gives you a unique number.
You are using aleph numbers incorrectly. aleph-1 is the infinity bigger than aleph-0. By the definition of aleph numbers, there is no such thing as aleph-1.5. I think what you are refering to is actually the beth numbers, where each beth number is defined as the cardinality of the power set of the previous one with beth-0 equal to aleph-0.
You’re absolutely right.
My bad, I was assuming the Generalized Continuum Hypothesis (like a damn fool!).
Gregory Chaitin’s Incompleteness Theorem
Gregory Chaitin proved a theorem similar to Gödel’s incompleteness theorems, and the framework of Chaitin’s version makes a lot more intuitive sense, I find. I don’t really understand the technicalities of these incompleteness theorems, but I do feel that Chaitin’s version is more enlightening.
Gödel’s incompleteness theorem says that, in any consistent axiomatic mathematical system, there will always be mathematical statements that can neither be proved true, nor proved false . That is, there will always be mathematical statements whose truth or falsity is undecidable – beyond the ability of the system’s axioms to determine.
However, Gödel never gives any sense of why this might be the case. Gödel does not even hint at the reason why the truth or falsity of some mathematical statements may within the grip of the axioms to determine, but other statements lie beyond the reach of the axioms.
Chaitin considers the algorithmic complexity of the axioms of mathematics. The algorithmic complexity of a string of data is defined as the shortest and most efficient program that can produce the string – ie, the most compressed representation of that data string.
I believe Chaitin showed that a given axiomatic mathematical system can only determine the truth or falsity of a mathematical statement if the algorithmic complexity of that statement is less than or equal to the algorithmic complexity of the set of axioms.
This makes more intuitive sense, and Chaitin’s theorem throws light on why there are mathematical statements that are not decidable: undecidable statements encode more information (algorithmic complexity) than do the axioms themselves; so the “spec” of the axioms is in effect insufficient to cover these mathematical statements of greater information content.
Chaitin says: if you have ten pounds of axioms, and a twenty-pound theorem, then that theorem cannot be derived from those axioms.
Another way I understand this is as follows:
When you prove a given mathematical statement to be true with respect to the axioms of a mathematical system, what you are really saying is that this mathematical statement is in accord with the foundational axioms, and this mathematical statement expresses some (but perhaps not all) of the information encoded in the axioms. (And if you prove the mathematical statement false, then you are just saying that the mathematical statement contradicts your axioms – but in either case, you have a definite answer).
However, when a mathematical statement contains more information than is found in the foundational axioms, it’s as if the axioms do not have sufficient “authority” to “adjudicate” upon the truth or falsity of such mathematical statements.
In the case of the continuum hypothesis being undecidable via the current axioms of mathematics, would I be right in thinking that Chaitin’s ideas suggest that the statement of the continuum hypothesis contains more information (algorithmic complexity) than does the entire current set of axioms of mathematics?
Further speculations:
Is it possible that a mathematical statement may be considered as an axiom in its own right, and so can, if you like, act as a axiomatic specification, in some way, of its own mathematical system?
If so, I wonder whether, when a mathematical statement contains more information than is found in the entire set of foundational axioms, it is possible to consider a complete role reversal, and instead ask if the “foundational axioms” can be proved true or false, with respect to the mathematical statement, this statement now raised the status of a defining foundational axiom?!
Might it also be possible to see whether working backwards in this way throws light on what augmentation of the foundational axioms might be necessary in order to make a given undecidable mathematical statement decidable?
In this way, could it be possible to work backwards from the statement of the continuum hypothesis, and see what enhancement of the current axioms of mathematics is necessary to make the continuum hypothesis decidable?
Hmm this doesn’t make any sense at all to me . You can’t have different sizes of
infinity because infinities have no size . Infinty to me means WITHOUT BOUNDS.
and if something has no boundary it cannot be sized .
Heres the mistake i see in the logic posted above .
Quote :- “There are infinities objectively bigger than the infinities so far. All of the infinities so far have been “countably infinite”, because they’re the same “size” as the counting numbers. Larger infinities can’t be paired, term by term, with smaller infinities.”
Why do you say the set of counting numbers have a size. ? Just because you
can count a small section of them (no matter how long you count for you have only counted a small section of them)doesnt mean the set has a size.They arent all countable of course becuz you never reach the end . So then if the set of positive integers has no size then all that follows above about “size” is also wrong.
You’re absolutely right, none of the infinities have a “size” the way we’re used to talking about it.
We define sets to be the same size if their elements can be paired up, and we define one set to be larger than another if not all of it’s elements cannot be paired up with the elements of the “smaller” set.
To show that a set is “countably infinite” you don’t actually have to do the counting, just show that it could be (given infinite time).
So, when you talk about the size of infinite sets it’s necessary to come up with a new idea of what size means.
Im still non the wiser sorry .I,m not an expert mathmatician but I have tried
to understand it since i saw a docu about it .The problem is the use of terms like
“size” “bigger and “smaller” .AS you clarify these words dont mean the same when used in this context as our normal understanding of them .IF so why then use these words ? wouldnt it make more sense to use or invent new words , rather than use ones that everyone has a good understanding off but are missused in this context.
Quote :- “To show that a set is “countably infinite” you don’t actually have to do the counting, just show that it could be (given infinite time).”
I have to take issue with any infinite set being countable, it isn’t , at least not the WHOLE set.Two infinties dont cancel each other out .Even if you had infinite time you still couldn’t count the WHOLE set of counting numbers . IT IS IMPOSSIBLE
to reach the end and thus count the WHOLE SET thats the very essence of the word “infinite” I believe.
.
Often mathematicians do make up new words, but for the purposes of this blog I try not to use them. It’s just one more thing to learn and keep track of. There’s a reason why “many-words-a-day” calenders don’t sell well.
Recognizing that the word “size” doesn’t cleanly apply to infinite things, mathematicians use the word “cardinality” instead. In fact, if you were so inclined, you could replace every instance of the word “size” with “cardinality” in this post.
It is frustrating that mathematicians talk about “counting to infinity”, while knowing that it’s impossible to actually do so. At the same time, it’s not like there are any surprises. You’re not going to get to a billion and six, and suddenly there’s a new number you weren’t expecting. So, you can talk about infinities without “doing the legwork”.
Could you explain why the cardinality of R should be the cardinality of the power set of N? I can’t imagine why that should be so.
Oh, I can explain this one! It’s pretty neat, actually.
Consider an arbitrary element of the power set of N — that is, consider an arbitrary set of natural numbers. Every natural number is either in this set or not in it. You could make a list of all the natural numbers and next to each number write “yes” if that number is in the set and “no” if it’s not, right? And that list would fully specify the contents of that set. So there is a one-to-one mapping between the set of such listings and the power set of N.
Okay now: Let’s notate those litsts a little differently. For “yes” write 1, and for “no” write 0. And put a decimal point at the beginning of the whole thing. You have just turned each set into a real number between 0 and 1, written in binary. So, there’s a mapping from the power set of N to [0, 1]. To turn this into a mapping to all of R, just feed it through a function that maps [0, 1] to the entirety of the reals, such as f(x) = tan((x-.5)*pi).
(Actually, there’s a slight problem with this, in that binary expansions have ambiguous representations just like decimal expansions: just as 0.99999… = 1.0, so too does binary 0.111111… So it isn’t quite a one-to-one mapping. Resolving this is left as an exercise for the reader.)
Basically to what I understand, in the end, there is only two types of infinite sets, the so-called countable set (integers, rationals, primes, etc., etc.) and un-countable sets, which is the set of real numbers, that’s it. Nothing in between them.
Another way to look at these two types of set is to consider one as “discrete set” and the other as “continuous set”, or “continuum”. Like our physical world, particularly in Electronics, there’s either Digital or Analogue, nothing in between, therefore, your set either falls under countable or un-countable, nothing in between. Like Quantum Mechanics and General Relativity, one explain our universe in “discrete form” while the latter in “continuous form”, which I think partly the reason why both can’t be fuse together.
Therefore, real numbers, in essence, are considered “continuous”, you really can’t draw a line between two real numbers, they just don’t exist. Therefore, there’s really no such sets of number which can be count and at the same time continuous. CH seems to be true in that sense.
Pingback: Basic math with infinity | Ask a Mathematician / Ask a Physicist
What about ‘many paths’ and probability, if seen in this light then? If I was to assume that before a outcome all possible paths are ‘taken’ . Would such ‘paths’ mathematically be considered finite, or infinite? Or could we define them to different ‘infinite sizes’ too? It’s not that I can’t see the point logically, but if I define the microscopicality that creates many paths as ‘time less’, then where is the infinity? Without a time existing, no space, and no matter either as far as I can see. Would such a thing be considered a infinity too?
I have to agree with K Davis for reasons similar to what he articulated. I posted a similar argument on my blog, Euclid5-Newton.