Q: Why does E=MC² ?

Posted on March 4, 2011 by The Physicist

Physicist: It’s a little surprising that this question didn’t come up earlier. Unfortunately, there’s no intuitive way to understand why “the energy of the rest mass of an object is equal to the rest mass times the speed of light squared” (E=MC²). A complete derivation/proof includes a fair chunk of math (in the second half of this post), a decent understanding of relativity, and (most important) experimental verification.

So first, here’s an old physics trick (used by old physicists) to guess answers without doing any thinking or work, and perhaps while drinking. Take everything that could have anything to do with the question (any speeds, densities, sizes, etc.) and put them together so that the units line up correctly. There’s an excellent example in this old post about poo.

Here’s the idea; energy is distance times force (E=DF), and force is mass times acceleration (E=DMA), and acceleration is velocity over time, which is the same as distance over time squared (E = DMD/T² = MD²/T²).

So energy has units of mass times velocity squared. So, if there were some kind of universal relationship between mass and energy, then it should depend on universal constants. Quick! Name a universal speed! E=MC²

Totally done.

This is a long long way from being a solid argument. You could just as easily have E=5MC² or E=πMC² or something like that, and still have the units correct. It may even be possible to mix together a bunch of other universal constants until you get velocity squared, or there may just be a new, previously unknown physical constant involved. This trick is just something used to get a thumbnail sketch of what “looks” like a correct answer, and in this particular case it’s exactly right.

For a more formal derivation, you’d have to stir the answer gravy:

Answer gravy: This derivation is going to seem pretty indirect, and it is. But that’s basically because E = mc² is an accidental result from a more all-encompassing theory. So bear with me…

The length of regular vectors, (which could be distance, momentum, whatever) remains unchanged by rotations. If you take a stick and just turn it, then of course it stays the same length. The same holds true for speed: 60 mph is 60 mph no matter what direction you’re moving in.

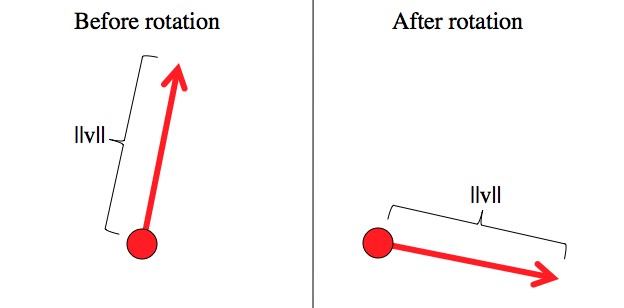
Although the vector, v, changes when you rotate your point of view, its length, ||v||, always stays the same.

If you have a vector (x,y,z), then it’s length is denoted by “ $||(x,y,z)||$ “. According to the Pythagorean theorem, $||(x,y,z)||^2 = x^2+y^2+z^2$ .

When relativity came along, time suddenly became an important fourth component: (x,y,z,t). And the true “conserved distance” was revealed to be: $||(x,y,z,t)||^2 = x^2+y^2+z^2-c^2t^2$ . Notice that when you ignore time (t=0), then this reduces to the usual definition.

This fancy new “spacetime interval” conserves the length of things under ordinary rotations (which just move around the x, y, z part), but also conserves length under “rotations involving time”. In ordinary physics you can rotate how you see things by turning your head. In relativity you rotate how you see things in spacetime, by running past them (changing your speed with respect to what you’re looking at). “Spacetime rotations” (changing your own speed) are often called “Lorentz boosts“, by people who don’t feel like being clearly understood.

You can prove that the spacetime interval is invariant based only on the speed of light being the same to everyone. It’s a bit of a tangent, so I won’t include it here. (Update 8/10/13: but it is included here!)

Some difficulties show up in relativity when you try to talk about velocity. If your position vector is $(x,y,z)$ , then your velocity vector is $\vec{v} = (\frac{\partial x}{\partial t},\frac{\partial y}{\partial t},\frac{\partial z}{\partial t})$ (velocity is the time derivative of position).

But since relativity messes with distance and time, it’s important to come up with a better definition of time. The answer Einstein came up with was $\tau$ , which is time as measured by clocks on the moving object in question. $\tau$ is often called “proper time”. So the better definition of velocity is $(\frac{\partial x}{\partial \tau},\frac{\partial y}{\partial \tau},\frac{\partial z}{\partial \tau}, \frac{\partial t}{\partial \tau})$ . This way you can talk about how fast an object is moving through time, as well as how fast it’s moving through space.

By the way, as measured by every one else on the planet, you’re currently moving through their time (t) at almost exactly 1 second per second ( $\frac{\partial t}{\partial \tau}=1$ ).

One of the most important, simple things that you can know about relativity is the gamma function: $\gamma = \frac{1}{\sqrt{1-\left(\frac{||v||}{c}\right)^2}}$ . You can derive the gamma function by thinking about light clocks, or a couple other things, but I don’t want to side track on that just now.

Among other things, $\gamma = \frac{\partial t}{\partial \tau}$ . That is, $\gamma$ is the ratio of how fast “outside time” passes from the point of view of the object’s “on-board time”. So now, using the chain rule from calculus:

$(\frac{\partial x}{\partial \tau},\frac{\partial y}{\partial \tau},\frac{\partial z}{\partial \tau}, \frac{\partial t}{\partial \tau}) = (\frac{\partial t}{\partial \tau}\frac{\partial x}{\partial t},\frac{\partial t}{\partial \tau}\frac{\partial y}{\partial t},\frac{\partial t}{\partial \tau}\frac{\partial z}{\partial t}, \frac{\partial t}{\partial \tau}) = (\gamma\frac{\partial x}{\partial t},\gamma\frac{\partial y}{\partial t},\gamma\frac{\partial z}{\partial t}, \gamma)$ .

For succinctness (and tradition) I’ll bundle the first three terms together:

$(\gamma\frac{\partial x}{\partial t},\gamma\frac{\partial y}{\partial t},\gamma\frac{\partial z}{\partial t}, \gamma) = (\gamma \vec{v}, \gamma)$

Now check this out! Remember that the spacetime interval for a spacetime vector with spacial component $\vec{a}$ , and temporal component $b$ , is $||(\vec{a},b)||^2 = a^2-c^2b^2$ .

$||(\gamma\vec{v}, \gamma)||^2 = \gamma^2v^2-c^2\gamma^2 = \gamma^2(v^2-c^2) = \frac{v^2-c^2}{1-\frac{v^2}{c^2}} = c^2\frac{v^2-c^2}{c^2-v^2} = -c^2$

(This used a slight breach of notation: “ $\vec{v}$ ” is a velocity vector and “ $v$ ” is the length of the velocity, or “speed”)

The amazing thing about “spacetime speed” is that, no matter what v is, $||(\gamma \vec{v}, \gamma)||^2 = -c^2$ .

(Quick aside; it may concern you that a squared quantity can be negative. Don’t worry about it.)

Now, Einstein (having a passing familiarity with physics) knew that momentum ( $\vec{P}$ ) is conserved, and that the magnitude of momentum is conserved by rotation (in other words, the direction of the momentum is messed up by rotation, but the amount of momentum is conserved (top picture of this post). He also knew that to get from velocity to momentum, just multiply by mass (momentum is $\vec{P}=m\vec{v}$ ). Easy nuf. $m^2||(\gamma \vec{v}, \gamma)||^2 = -m^2c^2 \Rightarrow ||(\gamma m\vec{v}, \gamma m)||^2 = -m^2c^2$

So if ordinary momentum is given by the first term (the “spacial term”): $\vec{P}= \gamma m \vec{v}$ , then what’s that other stuff ( $\gamma m$ )? Look at the conserved quantity:

$\begin{array}{ll} ||(\gamma m\vec{v}, \gamma m)||^2 = -m^2c^2 \\ \Rightarrow \left(\gamma mv\right)^2 - \left(\gamma mc\right)^2 = -m^2c^2 \\\Rightarrow P^2 - \left(\gamma mc\right)^2 = -m^2c^2 \end{array}$

What’s interesting here is that m²c² never changes, and P² only changes if you start moving. For example, if you were to run as fast as a bullet (in the direction of the bullet), you wouldn’t worry about it hurting you, because from your perspective it has no momentum.

So whatever that last term is ( $\gamma mc$ ) it’s also conserved (as long as you don’t change your own speed). Which is interesting. So the ‘Stein studied its behavior very closely. If you take its Taylor expansion, which turns functions into polynomials, you get this:

$\begin{array}{ll} m c \gamma\\= \frac{mc}{\sqrt{1-\left(\frac{v}{c}\right)^2}}\\= mc\left[1+\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\frac{5}{16}\frac{v^6}{c^6} \cdots \right]\\=mc+\frac{1}{2}m\frac{v^2}{c}+\frac{3}{8}m\frac{v^4}{c^3}+\frac{5}{16}m\frac{v^6}{c^5} \cdots \end{array}$

The second term there should look kinda familiar (if you’ve taken intro physics); it’s the classical kinetic energy of an object (1/2 mv²) divided by c. Could this whole thing (thought Einstein) be the energy of the object in question, divided by c? Energy is definitely conserved. And, since c is a constant, energy divided by c is also conserved.

So, multiplying by c: $E = \gamma m c^2 = mc^2+\frac{1}{2}mv^2+\frac{3}{8}m\frac{v^4}{c^2}+\frac{5}{16}m\frac{v^6}{c^4} \cdots$ .

You can also plug this into $P^2 - \left(\gamma mc\right)^2 = -m^2c^2$ and, Alaca-math! You get Einstein’s (sorta) famous energy/momentum relation: $P^2c^2 + m^2c^4 = E^2$ .

Notice that the energy and momentum here are not the classical (Newtonian) energy and momentum: $E=\frac{1}{2}mv^2$ and $\vec{P} = m\vec{v}$ . Instead they are the relativistic energy and momentum: $E=\gamma mc^2$ and $\vec{P} = \gamma m\vec{v}$ . This only has noticeable effects at extremely high speeds, and at lower speeds they look like: $E \approx mc^2 + \frac{1}{2}mv^2$ and $\vec{P} \approx m\vec{v}$ , which is what you’d hope for. New theories should always include the old theories as a special case (or disprove them).

Now, holy crap. If you allow the speed of the object to be zero (v=0), you find that everything other than the first term in that long equation for E vanishes, and you’re left with (drumroll): E=mc²! So even objects that aren’t moving are still holding energy. A lot of energy. One kilogram of matter holds the energy equivalent of 21.4 Megatons of TNT, or about 1500 Hiroshima bombs.

The first question that should come to mind when you’ve got a new theory that’s, honestly, pretty insane is “why didn’t anyone notice this before?” Why is it that the only part of the energy that anyone ever noticed was $\frac{1}{2}mv^2$ ? Well, the higher terms are a little hard to see. Up until Einstein that fastest things around were bullets moving at about the speed of sound. If you were to use the “ $\frac{1}{2}mv^2$ ” equation for kinetic energy you would be exactly right up to one part in 20,000,000,000,000,000. All of the higher terms are divided by some power of c (a big number), so until the speed gets ridiculously high they just don’t matter.

But what about the mc²? Well, to be detected energy has to do something. If somebody flings a battery at you, it really doesn’t matter if the battery is charged up or not.

Side note: This derivation isn’t a “proof” per say, just a really solid argument: “there’s this thing that’s conserved according to relativity, and it looks exactly like energy”. However, you can’t, using math alone, prove anything about the outside universe. The “proof” came when E=mc² was tested experimentally (with particle accelerators ‘n stuff).

But Einstein’s techniques and equations have been verified as many times as they’ve been tested. One of the most profound conclusions is that, literally, “energy is the time component of momentum”. Or “E/c” is at least. So conservation of energy, momentum, and matter are all actually the same conservation law!

This entry was posted in -- By the Physicist, Physics, Relativity. Bookmark the permalink.

82 Responses to Q: Why does E=MC² ?

J-Rad says:

December 27, 2013 at 4:04 am

In your response above you stated as follows:

The exact expression is floating around somewhere in the middle of the post. The energy is E = \frac{mc^2}{\sqrt{1-\left(\frac{v}{c}\right)^2}} = mc^2 + \frac{1}{2}mv^2 + \frac{3}{8}m\frac{v^4}{c^2}+\cdots, with more and more terms that are less and less important.
So, the approximation E=mc^2+\frac{1}{2}mv^2 is pretty good, but isn’t exact.

I’m an engineer and noticed that this looks extremely similar to Bernoulli’s Principle for fluid dynamics (http://en.wikipedia.org/wiki/Bernoulli's_principle).

Assuming I consider mc^2 to be a constant potential energy within the object, or the gz term in Bernoulli; the (mv^2)/2 being the kinetic energy imparted by motion. Would I be correct to consider the remainder of the equation to be similar to the energy due to pressure? If so, what sort of pressure would this be referring to? Does it relate to the pressure from mass increasing infinitely as it approaches the speed of light?

The more I think about this, the more confused I’m becoming.
Pierre Beaudet says:

December 29, 2013 at 2:41 pm

There must exists a relationship between this formula and the kinetic energy of this mass in movement described as 1/2mv.v. So if a mass is moving at the speed of light, why is its kinetic energy only half of what the energy of the rest mass calculated by the Einstein formula ?
mohammad riaz khan says:

February 16, 2014 at 10:45 pm

Please try to avoid confusion,& then ur thinking may come true & fruitful.u may contact me if u r interested to avoid confusion.As u mentioned u r an engineer so i m (B.Sc. electrical engg.70 uet lhr.easier contact is 03335337077 Islamabad.
PacRim Jim says:

April 8, 2014 at 3:36 am

You, sir, are a witty writer.
James Kirk says:

May 1, 2014 at 4:59 pm

Just thought I’d add to this, as I’m still a little confused about the answer, and if history has taught me anything it’s if something doesn’t make sense, there’s either some piece of information you’re missing, or it’s wrong. So my question is, why based on the theory that energy is matter, do we have to put a “C^2” on the end? Why can’t we just say energy is mass in a different state and be done with it? Is it just so the formula’s work out? If energy and mass are 2 things in different states, then why do they have to be multiplied by anything? It’s like saying a basketball is twice as good as the emotion ‘fear’. They are both completely unrelated. Assuming that mass has to be multiplied by something means that we must have known that mass was relative to energy in the first place. A little side track here, but why don’t we assume it’s the other way round? If a kg of mass has the same energy as an atomic bomb, based on my ideas of mass and energy relativity would make me assume that actually mass is much greater in magnitude than energy, as contained with in that mass is a great amount of energy, therefore M=E(some random high number)^2
Xerenarcy says:

May 2, 2014 at 3:25 am

@James
a very simple explanation is the units used. it is possible, but cumbersome, to write the above using ‘natural’ units, where all the constants of nature are reduced to 1 and just omitted for simplicity. the relations would still be just as true but the scales would vary too much to be of use – we are stuck with seconds, kg, meters and so on because they’re familiar on our scale of experience. eg, you wouldn’t talk about light-seconds as units of distance in every-day language (i travel 0.0002 ls to work and back, you might drive at 0.0003 ls/h) even though this is perfectly (perhaps more) correct.

although no one will ever tell you the duration of a day is 0.000288 meters-per-lightspeed. i hope.

funny enough, the meter (for instance) is presently defined exactly this way, as a function of the speed of light and some constant, miniscule duration (transition of states of cesium atom or something like that).
James Kirk says:

May 3, 2014 at 7:14 am

So you’re saying that the C^2 is just to make it all work out to the scales humans are used to, and is in fact irrelevant if you aren’t actually working anything out based on it and want to understand the formula.

What i mean is, if someone were to say to me “what does e=mc^2 mean” i could just say “energy is matter”
Error: Unable to create directory uploads/2024/12. Is its parent directory writable by the server? The Physicist says:

May 3, 2014 at 10:56 am

@James Kirk
Nope! If you follow the “c²” all the way back you find that it enters the calculation in the “spacetime metric”, which describes the “time distance” as the distance that light travels over a given time interval. Ultimately, the reason that the metric is useful and takes that particular form is that the speed of light is the unique speed that is invariant. If aliens (with completely different units for things) figured things out as far as we have, they’d come up with the same equation.
Optimistic Pessimist says:

May 26, 2014 at 12:19 am

@The Physicist

My biggest question that I have found unanswered (possibly unanswerable by human current technological observation and measurement), is that why do we assume our observation of the “constant” state of the speed of light are in the slightest relevant to anyone or anything but ourselves? In the same scenario, aliens with different units have figured things out as far as we have, may and quite possibly have a more advanced equation based on their natural perception/ technological measurement. Basically, my question boils down to a similar situation of Newtonian meets quantum physics, in an obscure way. How do we know the speed of light is constant, outside our observable range, how could we test if there even is something out of our observable range, and how would we be able to test for it if by our standards it is not able to be quantified? (E.X. aliens perceive time at a much more precise rate (and quantify it to said rate) In this scenario infinitesimally small differences in the speed of light in the unobservant but theorized universe (within our understanding) Wouldn’t ((c^c+1×10-infinite by our standards) Completely change our understanding (assuming we could understand it) of E=M(c^2)))? @ James Kirk, this is why I have to agree that it is a gross oversimplification, similar to our current knowledge of macro vs. micro physics. c^2 seems random and arbitrary to our current knowledge that so happens to fit our “observable” conditions. Truly a scientific mystery to me, is how the more I learn, the less I realize we think we know. I hope to live to see the day that the smallest possible scale of existence is combined into a macro/micro grand unification theory. As of this moment in “time” it seems as though all existence is simply a matter of perception, to the point where our objective measurements are subjective to the nature of the “whole” universal picture.

We observe X,Y,Z coordinates and are aware of our linear travel through the T coordinate. Isn’t it possible, neigh probable, that intelligence other than our own has surpassed this as low level knowledge, compiling X,Y,Z,T,???? into their own unification theory? I realize this is pure speculation scientifically at this point (though what truth has not been scrutinized as fallacy or magic throughout the ages?), but I fell as though if it were taught as a part of physics, the idea that our observations are most likely flawed and inaccurate would give us these answers faster. If history is any guide (and in many Human ways it is) than we should be aware that the biggest obstacle is our own ignorance of that which has yet to be postulated and measured true.

I’ve gone the old ways, and ranted drunkenly, philosophically at the universe, straying every way from my main question, which could be any one of these currently unmeasured, non-quantifiable, hypothetical situations I’ve postulated.

I do not expect an answer, but am left wondering, why are these, the greatest and most important questions of existence, given such a small sum of our current resources when it is clearly a future based not on the mistakes of the past? Such is life in my mind….any comments gladly welcomed.
Mark says:

June 14, 2014 at 2:51 pm

Too James Kirk RE “What does e=mc^2 mean” Could U just say “energy is matter?”
No you could not. That answer would be incomplete in that it does not convey how much matter.

The statement “Energy is Matter” isn’t correct technically because while you can convert between energy and matter, they are different things. It’d be like saying Ice is Steam. You can convert from Ice to Steam and they certainly have a common underlying structure, but they aren’t the same!

Your statement “Energy is Matter” also kind of implies that they are stored in each other in equal quantities. This misses the meaning of E=MC2 in that there is a LOT of energy in matter, and more precisely that the amount of Energy is exactly and precisely the amount of Mass times the square of the speed of light.

To the underlying question asked in this post.. WHY Does E=MC2 and more specifically why is that C2 factor there?

The answer I believe is in Einstein’s discovery of the Space-Time continuum, in which they are different dimensions/aspects of the single reality in which we live.

If I were to ask you, why is the Area of a Square=Length Squared, you’d say because when you extend a line into the 2nd dimension the number of units have to be multiplied by itself to take account for that whole new dimension the line is extending into.

The concept of SpaceTime is similar. Our 3 dimensional concept of distance (H*W*D) is augmented by Einsteins revelation that Time is a 4th dimension that exists at right angles to our normal concept of “space”.

This how velocity in Einsteins earlier equation can be used with a simple right triangle to relate the right-angle aspects of time to space, and thus mass to energy. It’s only one minute long!
John Smith says:

June 17, 2014 at 11:02 pm

@The Physicist
Excellent job ! Thank you for this very important contribution!

@Pierre Beaudet
The v in this page is the speed of the person who pass by the mass and look at it. It is NOT the speed of the mass. In E=mc*c the observer who looks at m is passing by at the speed of v (in E=mc*c the observer is not moving so actually v is 0). While, the kinetic energy E=1/2 mv*v of normal physic is for a mass going at the speed of v. So it is not the same situation at all. Never compare those equation. Here c is NOT even a speed…it is a constant.

@James Kirk
If you accelerate a mass of 1 kg over a distance of 1 meter, you used 1 joule of Energy.(Work=Force*distance) Any machine can do this, but the Energy is the same. Energy is not a reality, it is only a definition. The only reality is that a mass will be accelerated over a distance of 1 meter. You cannot buy Energy. But you can buy a machine that can accelerate a mass. (Like a rocket). Knowing this you see that Energy and mass have nothing in common.

If you pass real fast an object you have to see it behave exactly the same as if you don’t move when you look at it. In order for this to be true you have to try to pass the object at a speed that is close to c (It cannot be faster then c). For example, you can try to pass the object at the speed of v (v is the observer speed, not the object speed) and you look at the mass. We know now that the object length will contract and time will take longer (dilatation of time). After all the math on this page we get E=mc*c. c is not the speed of the object but a constant that is CONSTANT for the universe. We can’t go faster then c. Here the mass is not moving, c is not its speed. And the observer is not moving, so v is 0.

What kind of machine would produce that energy ? We can use the dissintegration of Uranium to liberate the mass of the uranium into a force capable of accelerating the other mass around it over many kilometers (This is what energy is: accelerating mass over a distance). Like an explosion of slinky each mass pushing into the others. The mass liberated push the mass all around it over great distance.The accelerating mass over distance in the explosion is what is call the Energy.

Energy is a fancy name to describe a mass moved around by some process or machine.
Jeffrey Greenspan says:

July 3, 2014 at 2:46 pm

In the Equation E=mc2, is it saying that the mass is moving at the speed c2? If so, how is that possible?
Tarun says:

December 22, 2014 at 11:28 pm

sir,How to break
E=MC*C
David Martin says:

January 27, 2015 at 4:00 am

You can derive it in a few different ways out of other physics we have, and out of some mathematics that we have. But we have no explanation, and the correct answer is ‘we don’t know’. Matter has a rest energy, and relativistic energy, proportional to its rest mass and its relativistic mass – so its energy increases in a frame in which it is moving. We don’t know why.

It’s important to tell physics students honestly when we don’t know something, as one day one of them might find a new explanation. They should feel there’s good reason to think about it in that kind of way. If you often talk as if we know as much as can be found out about things, as you do, that will make them feel it’s not worth looking for an explanation, and it shuts down the search. But the search is what physics is all about.
Ray Righetti says:

January 28, 2015 at 1:06 am

The constants and variables and their ratios to each other are not arbitrary!
A specific amount of mass is completely converted to a specific amount of energy based on E=MC^2, (not 1/2 or 1/4 or 10 x). The correct answer is obtained exactly as the equation predicts, but only when the proper (complimentary) units of measure are employed through out the equation. In the English units of measure system for example, if energy is expressed in ft-lb. , then mass would be expressed in “slugs” which has the units of (lb-sec^2/ft), and speed of light would be expressed in in ft/sec. In the whole of of engineering and the sciences, consistency of the units of measure, or dimensional similitude, is absolutely imperative to arrive at the correct answer. When dimensional similitude is exercised, the answer will contain the correct quantity expressed in the correct units of measure.
Stuart Shepherd says:

February 2, 2015 at 7:21 pm

Totally, totally fantastic article and presentation! I can’t remember when I both enjoyed a scientific presentation and, at the same time, was so confident in its’ veracity by virtue of the strength, logic, and manner of presentation. A physicist with a sense of humor and real, real intelligence. Kind of like Einstein himself. He was a very funny guy, enjoyed life, and also had a whole lot of wisdom. Read his quotes. But I really got a lot out of THIS presentation- intellectually- because the author showed his true humanity which, in THIS case, is quite brilliant!
Pablo Jeynes says:

April 24, 2015 at 10:35 am

If you take a reflecting box with light inside.. an electromagnetic wave bouncing back and forth, if you try to push or accelerate the box the em radiation pressure on the inside walls makes the box behave as though it had an inertial mass given by the electromagnetic energy divided by c squared. The calculation is straightforward in 1d.
The electromagnetic theory needs no modification for Einstein relativity so this works out easily.
This is one thought experiment which supports equivalence of mass and energy.
There are many such.
A simple theoretical spacetime argument follows. The invariant spacetime interval s2= x2+y2+z2-t2 implies a 4 vector xyzt with a minus sign on the 4th time like component of the Pythagoras equivalent. (Note c=1 units)
Also recall momentum is force by time and energy is force by distance.
Space-time 4 vector thus implies momentum-energy 4 vector.
Differentiating the space-time 4 vector leads to a velocity 4 vector, then multiply by mass gives momentum energy 4 vector where -m2=px2+py2+pz2-E2.
Thus for momentum zero then E=m or restoring units E=mc2. Qed:)
Pablo Jeynes says:

April 24, 2015 at 11:59 pm

Errata. I’ve got a minus sign problem ..from having mixed the two usual sign conventions. Also I used a web notation with c2 meaning c squared.
outsidethebox says:

May 1, 2015 at 10:43 pm

Alright. I have 1 gram of pure coal and E=MC2 it. How much energy do I get? Metric system please.
Pablo Jeynes says:

May 7, 2015 at 10:29 am

mass 1 gram = 0.001 kg in SI units
constant c is the time space conversion factor which has units of velocity and light probably travels at exactly or near to this universal constant ( assumes light photon has zero rest mass) c = 3 x ten to power 8.
Thus energy E = mc2 gives .001x3x3x10^16 = 9 x 10 to power 13 joules.
or 90 000 000 000 000 J ….which is 90 trillion joules (us/uk trillions or spanish billions).
one joule is one newton metre. Since there are g= 9.8~10 newton in a kilogram we see there is enough energy to raise a big 90 kg bloke vertically upwards through a distance of 9 x 10^13/10 /90 = 10 ^11 metre or 10 ^ 8 km = 100 million kilometres.

Assuming world population of 10 ^10 we see 1 gram of material (a small leaf) would provide enough energy to raise the whole of humanity upward by 10 metres!

Hope i didnt drop any powers of ten anywhere.
Eugene No says:

May 27, 2015 at 1:34 am

The mass of the 2 can come out with the mass times of the speed of light squared. The way of works is energy is the distance times the force. E=mc^2.
Eugene No says:

May 27, 2015 at 1:36 am

The speed of the light can be form is the quickest universal speed.
H Martinez says:

June 11, 2015 at 7:40 pm

My question is: My understanding is that the Higgs particle is what gives all other particles their mass and the Higgs had not been theorized; How was Einstein able to derive the E=mc^2 since mass was an unknown? What am I missing?
Pablo Jeynes says:

June 18, 2015 at 5:26 pm

The basic energy-mass equivalence of Einstein in no way rests on the advanced quantum field theoretic Higgs particle. The common electromagnetic field suffices. We can think of microwaves as a familiar example.
One might initially suppose the idea of mass would be irrelevant for such invisible wavy phenomena which manifest little in the way of solid material form. However experiment and theory easily shows EM waves exert force like pressure on objects in their path like reflecting walls on microwave oven or light pressure on dust or ice particles in cometary tails. So EM waves do carry energy and momentum, from Faraday to Maxwell Lorentz theory we get that electromagnetic wave energy equals momentum times c (the speed of all em waves including light) E=pc.
Already in Newtonian mechanics we would assume that having momentum would need material or mass. Curiously Einstein relativity allows zero mass particles to carry energy and momentum related by E=pc . If a collection of zero mass particles (photons) are trapped in box , then by very simple energy momentum analysis and reflection from walls, the box as a whole is easily seen to behave as though it does actually possess statistically an inertial mass given by the total energy divided by c^2.
Alternatively one can use the EM field equations to get the same result (without statistics and photons.)
So the ethereal EM field energy results in an effective inertial mass given by M = E/c^2.
Lots more hypothetical situations require generalisation of this mass energy equation into what is really an equivalence. Any energy type anywhere will equivalently be an inertial and gravitational mass and vice versa. A hot cup of tea loses weight getting lighter very slightly as it loses heat. Chemical reaction products weigh very slightly less than initial reactants for exothermic case. ….it s not only in nuclear reactions though of course the energies are several orders different.
Steven vaca says:

August 20, 2015 at 7:07 pm

What would happen if we applied the laws of science to the equation, like every action having an equal and opposite reaction. So if we are adding the speed of light then we need to add the speed of dark. So instead of e=mc^2, we use my version e=mc^-2. That’s the same equation I used to potentially create fire by friction in space
Luigi says:

October 26, 2015 at 8:04 pm

Hello,
Maybe someone asked this question before, I can’t find the answer, my apologies.
In the Universe no object can’t go faster than the speed of light, so how come we are squaring the speed of light for E=MC^2?
We are assuming that Mass is Energy when it goes the square of the speed of light?
Thank you!
Luigi
Angel says:

November 25, 2015 at 8:27 pm

@H Martinez

Mass wasn’t unknown. What was unknown what interpolation of a particle function gave rise to the property of mass. But what mass itself was supposed had been known since antiquity.
Lance Brainstrong says:

April 10, 2016 at 10:08 pm

All this brilliance and still no one quite knows how a bicycle works! Id est: how come one can only balance on a bike (unless they’re a real clutz) when moving forward? I have a theory of sorts, but words are my trade, not numbers.

JS
SlimeyOne says:

October 3, 2019 at 10:01 pm

E = mc^2 :
E : Energy, in joules (J) = ( 9 x 10^16 J)
m : mass, in kilograms (kg) = 1 kg or ( 1 x 10^0 kg)
c^2 : velocity of light (squared), in meters per second (m/s) = ( 9 x 10^16 m/s)
E = mc^2 : E ( 9 x 10^16 J) = m ( 1 x 10^0 kg) x c^2 ( 9 x 10^16 m/s)
NOTE: c : “celeritas”, Latin for “swift”, for the velocity of light (in a vacuum)
c = 299,792,458 meters per second rounded to (3 x 10^8 m/s)
The velocity of light, squared:
c^2 = 89,875, 517,873,681,764 meters per second, rounded to (9 x 10^16 m/s)

The way it is written, E = mc^2 means that it would take 90,000 trillion joules
(9 x 10^16 J) of energy to lift a mass of 1 kg a distance of 300 million meters
in 1 second (3 x 10^8 m/s).

It actually means that a mass of 1 kg of matter (ANY kind of matter)
contains (9 x 10^16 J) energy.

ALL matter is made of atoms that contain “nucleons”,
a term for protons and neutrons.
Each nucleon contains ( 1.5 x 10^-10 J) of energy.
A mass of 1 kg of matter consists of ( 6 x 10^26 nucleons).

All the energy in 1 kg of matter (any kind of matter):
( 6 x 10^26 nucleons) x ( 1.5 x 10^-10 J) = ( 9 x 10^16 J).
Thus: 1 kg of matter = ( 9 x 10^16 J) of energy.
( 9 x 10^16 J) of energy = 21.5 Megatons of TNT.
This is 1,000 greater than the atom-bomb attack on
Nagasaki, Japan on August 9th, 1945.
Pingback: SR&ED Legal Analysis – The Life Choice Case | Bond Consulting Group
Pingback: SR&ED Legal Analysis - The Life Choice Case - Bond Consulting Group
constance sturm says:

December 5, 2024 at 1:40 pm

question: can E=mc cubed be realized in a different dimension such as 4th. Like in some of Picasso’s paintings?

Q: Why does E=MC² ?

82 Responses to Q: Why does E=MC² ?

Leave a Reply Cancel reply

Send your questions about math, physics, or anything else you can think of to:

Subscribe via Email

Search the Archives

Categories

Archives

Recent

Q: Why does E=MC2 ?

82 Responses to Q: Why does E=MC2 ?

Leave a Reply Cancel reply

Send your questions about math, physics, or anything else you can think of to:

Subscribe

Subscribe via Email

Search the Archives

Categories

Archives

Recent

Q: Why does E=MC² ?

82 Responses to Q: Why does E=MC² ?